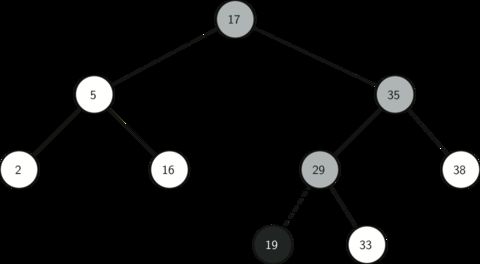
二叉搜索树 python实现

Python数据结构————二叉查找树的实现

对于二叉查找树的每个节点Node，它的左子树中所有的关键字都小于Node的关键字，而右子树中的所有关键字都大于Node的关键字。

二叉查找树的平均深度是O(log N)。

1.初始化

class  BinarySearchTree( object ):
    def  __init__( self ,key):
        self .key = key
        self .left = None
        self .right = None

2.Find

def  find( self ,x):
    if  x = = self .key:
        return  self
    elif  x< self .key  and  self .left:
        return  self .left.find(x)
    elif  x> self .key  and  self .right:
        return  self .right.find(x)
    else :
        return  None

3.FindMin和FindMax

分别返回树中的最小元素与最大元素的位置。FindMin，从根开始并且只要有左儿子就向左进行查找，终止点是最小元素。FindMax则向右进行。

def  findMin( self ):
    if  self .left:
        return  self .left.findMin()
    else :
        return  self
def  findMax( self ):
    tree = self
    if  tree:
        while  tree.right:
            tree = tree.right
    return  tree

4.Insert

为了将x插入到树Tree中，先用find查找，如果找到x，则什么也不做。否则，将x插入到遍历路径的最后一点。

来自《Problem Solving with Algorithms and Data Structures》的图片：

def  insert( self ,x):
    if  x< self .key:
        if  self .left:
            self .left.insert(x)
        else :
            tree = BinarySearchTree(x)
            self .left = tree
    elif  x> self .key:
        if  self .right:
            self .right.insert(x)
        else :
            tree = BinarySearchTree(x)
            self .right = tree

5.Delete

删除某节点有3种情况：

5.1 如果节点是一片树叶，那么可以立即被删除。

来自《Problem Solving with Algorithms and Data Structures》的图片：

5.2 如果节点只有一个儿子，则将此节点parent的指针指向此节点的儿子，然后删除。

来自《Problem Solving with Algorithms and Data Structures》的图片：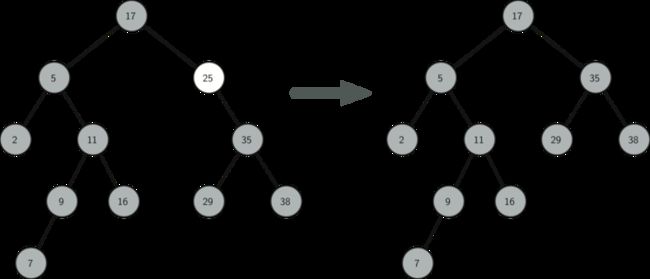

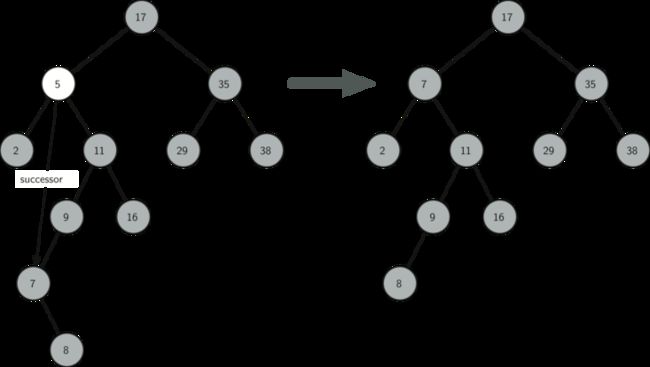
5.3 如果节点有两个儿子，则将其右子树的最小数据代替此节点的数据，并将其右子树的最小数据（不可能有左儿子，只有一个右儿子）删除。

来自《Problem Solving with Algorithms and Data Structures》的图片：

def  delete( self ,x):
    if  self .find(x):
        if  x< self .key:
            self .left = self .left.delete(x)
            return  self
        elif  x> self .key:
            self .right = self .right.delete(x)
            return  self
        elif  self .left  and  self .right:
            key = self .right.findMin().key
            self .key = key
            self .right = self .right.delete(key)
            return  self
        else :
            if  self .left:
                return  self .left
            else :
                return  self .right
    else :
        return  self

全部代码

class  BinarySearchTree( object ):
    def  __init__( self ,key):
        self .key = key
        self .left = None
        self .right = None
    def  find( self ,x):
        if  x = = self .key:
            return  self
        elif  x< self .key  and  self .left:
            return  self .left.find(x)
        elif  x> self .key  and  self .right:
            return  self .right.find(x)
        else :
            return  None
    def  findMin( self ):
        if  self .left:
            return  self .left.findMin()
        else :
            return  self
    def  findMax( self ):
        tree = self
        if  tree:
            while  tree.right:
                tree = tree.right
        return  tree
    def  insert( self ,x):
        if  x< self .key:
            if  self .left:
                self .left.insert(x)
            else :
                tree = BinarySearchTree(x)
                self .left = tree
        elif  x> self .key:
            if  self .right:
                self .right.insert(x)
            else :
                tree = BinarySearchTree(x)
                self .right = tree
    def  delete( self ,x):
        if  self .find(x):
            if  x< self .key:
                self .left = self .left.delete(x)
                return  self
            elif  x> self .key:
                self .right = self .right.delete(x)
                return  self
            elif  self .left  and  self .right:
                key = self .right.findMin().key
                self .key = key
                self .right = self .right.delete(key)
                return  self
            else :
                if  self .left:
                    return  self .left
                else :
                    return  self .right
        else :
            return  self

上述写法的缺点是很难处理空树的情况。

另一种类似于链表的写法

class  TreeNode( object ):
    def  __init__( self ,key,left = None ,right = None ,parent = None ):
        self .key = key
        self .left = left
        self .right = right
        self .parent = parent
    def  hasLeftChild( self ):
        return  self .left
    def  hasRightChild( self ):
        return  self .right
    def  isLeftChild( self ):
        return  self .parent  and  self .parent.left = = self
    def  isRightChild( self ):
        return  self .parent  and  self .parent.right = = self
class  BSTree( object ):
    def  __init__( self ):
        self .root = None
        self .size = 0
    def  length( self ):
        return  self .size
    def  insert( self ,x):
        node = TreeNode(x)
        if  not  self .root:
            self .root = node
            self .size + = 1
        else :
            currentNode = self .root
            while  True :
                if  x
                    if  currentNode.left:
                        currentNode = currentNode.left
                    else :
                        currentNode.left = node
                        node.parent = currentNode
                        self .size + = 1
                        break
                elif  x>currentNode.key:
                    if  currentNode.right:
                        currentNode = currentNode.right
                    else :
                        currentNode.right = node
                        node.parent = currentNode
                        self .size + = 1
                        break
                else :
                    break

    def  find( self ,key):
        if  self .root:
            res = self ._find(key, self .root)
            if  res:
                return  res
            else :
                return  None
        else :
            return  None
    def  _find( self ,key,node):
        if  not  node:
            return  None
        elif  node.key = = key:
            return  node
        elif  key
            return  self ._find(key,node.left)
        else :
            return  self ._find(key,node.right)
    def  findMin( self ):
        if  self .root:
            current = self .root
            while  current.left:
                current = current.left
            return  current
        else :
            return  None
    def  _findMin( self ,node):
        if  node:
            current = node
            while  current.left:
                current = current.left
            return  current
    def  findMax( self ):
        if  self .root:
            current = self .root
            while  current.right:
                current = current.right
            return  current
        else :
            return  None
    def  delete( self ,key):
        if  self .size> 1 :
            nodeToRemove = self .find(key)
            if  nodeToRemove:
                self .remove(nodeToRemove)
                self .size - = 1
            else :
                raise  KeyError, 'Error, key not in tree'
        elif  self .size = = 1  and  self .root.key = = key:
            self .root = None
            self .size - = 1
        else :
            raise  KeyError( 'Error, key not in tree' )
    def  remove( self ,node):
        if  not  node.left  and  not  node.right:    #node为树叶
            if  node = = node.parent.left:
                node.parent.left = None
            else :
                node.parent.right = None

        elif  node.left  and  node.right:    #有两个儿子
            minNode = self ._findMin(node.right)
            node.key