问题如下: leetcode 587
在一个二维的花园中,有一些用 (x,y) 坐标表示的树。由于安装费用十分昂贵,你的任务是先用最短的绳子围起所有的树。只有当所有的树都被绳子包围时,花园才能围好栅栏。你需要找到正好位于栅栏边界上的树的坐标。
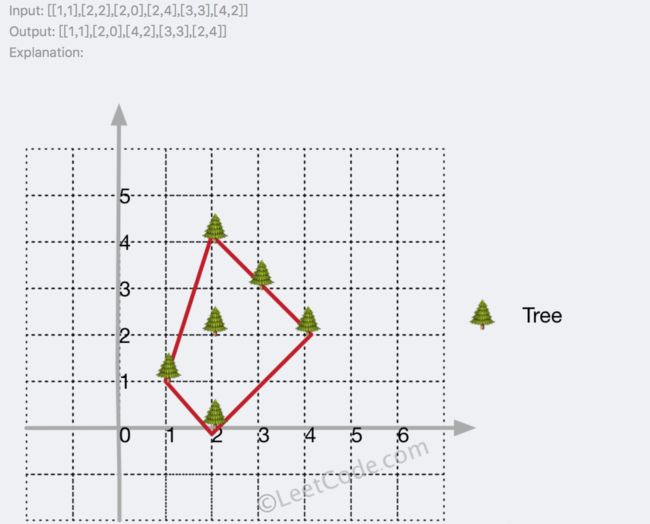
解法一:暴力解法
我们知道凸包的性质,凸包一定是【最外围】的那些点圈成,所以假设有n个点,那么最多可以构造出n(n−1)2条边,算法如下:
1. 选定一条边,遍历其他n-2个点,如果所有点都在该条边的一侧,则加入凸包集合。
2. 不断重复步骤1,直到所有边都被遍历过。
如何判断一个点 p3 是在直线 p1p2 的左边还是右边呢?(坐标:p1(x1,y1),p2(x2,y2),p3(x3,y3))我们可以计算:
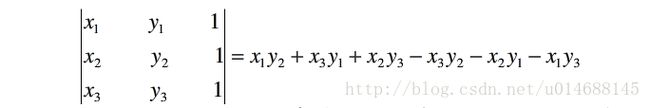
当上式结果为正时,p3在直线 p1p2 的左侧;当结果为负时,p3在直线 p1p2 的右边。
#include
#include
#include
#include
#include
#include
#include
#include
解法二:Graham扫描法

第一步:找y最小的点(如果相等就找其中x最小的)作为基准点P0。
第二步:把所有点的坐标平移一下,使 P0 作为原点,如上图。
第三步:计算各个点相对于 P0 的幅角 α (弧度),按从小到大的顺序对各个点排序。
当 α 相同时,分条件考虑:
如果当前弧度是最大弧度,说明在最左边边界,距离 P0 比较远的排在前面。
如果当前弧度是最小弧度,说明在最右边边界,距离 P0 比较近的排在前面。
如果在中间,那就都可以。
例如上图得到的结果为 P1,P2,P3,P4,P5,P6,P7,P8。我们由几何知识可以知道,结果中第一个点 P1 和最后一 个点 P8 一定是凸包上的点。
第四步:我们已经知道了凸包上的第一个点 P0 和第二个点 P1,我们把它们放在栈里面。现在从步骤3求得的那个结果里,把 P1 后面的所有点拿出来做当前点,遍历进行第五步。
第五步:连接栈顶的第二个点和栈顶的那个点,得到直线 L 。
看当前点是在直线 L 的右边还是左边。
如果在直线的右边就说明现在栈顶的点不是凸点,将栈顶的点弹出。当前点不变。
如果在直线上,或者在直线的左边,说明当前栈顶的点是满足条件的,把当前点入栈。遍历后一个点。
第六步:当把步骤3求得的结果里的所有点都遍历完了,还剩在栈里面的点就是凸点。导出即可。
代码如下:
#include
#include
#include
#include
#include
#include
#include
#include
关于leetcode 587的问题:
上面的代码跑587在
[[0,0],[0,1],[0,2],[1,2],[2,2],[3,2],[3,1],[3,0],[2,0]] 会报错。
但是单独调试这个实例又是正确的答案。所以很困惑。
![]()

