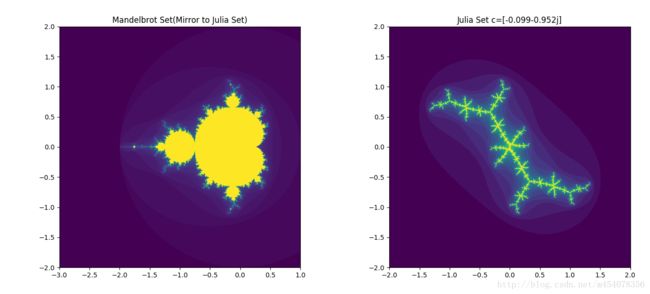
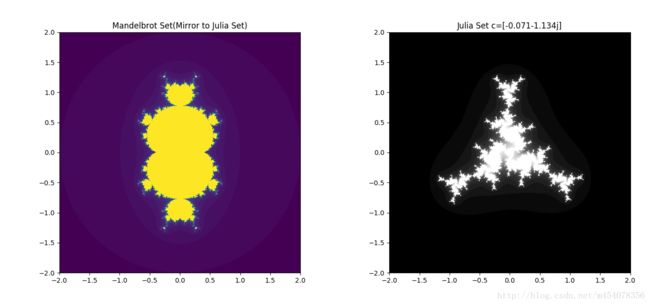
Python绘制Mandelbrot Set与Julia Set
看了这篇文章感觉画出一个分形并不是想像的那么难,并且被这美丽而又统一的图案深深的吸引了。所以决定用Python绘Mandlebrot Set和Julia Set。因为两个集合是同一个式子的不同参数的递归,并且Mandlebrot是对Julia的一种概括,可以点击Mandlebrot Set中的一点,观察对应Julia Set的变化或许更为直观,也更能体会两者其中美妙的关联。
计算思路
Mandlebrot Set 与 Julia Set都是对z^2+c的迭代,不同的是,Mandlebrot Set是将复平面每一点带入c,z的初始值为0。Julia Set是将复平面的每一个值带入z,c是一个固定值有我们点Mandlebrot Set上的一点得到。c决定了Julia Set的形状,Mandlebrot Set便是选取所有的c在z=0时的切片,包含了所有的Julia Set的特征。这个式子有四个参数控制,分别是z,c的实部和虚部,两个集合分别是这个四维图像的投影。
如何上色
一般不采取迭代一定次数后|z|对应到Color Map,那样颜色很杂乱,到最后的结果会很难受。只需要采取很简单的方法就可以做到,就是使用逃逸速度,对每一点进行迭代,|z|大于2的时候就知道继续迭代下去肯定发散,记录此时已经迭代的次数,对应Color Map即可。
前提
安装matplotlib和numpy,Anaconda已经包含这些。matplotlib包含了简单的color map,直接用就好了,看起来也很漂亮。numpy则是可以直接像matlab一样对所有的元素进行计算,速度快而且简单。
import numpy as np
import matplotlib.pyplot as plt
julia_C = -0 + 0j
def julia_set(x, y):
z = np.array(x + 1j * y)
r = np.zeros(z.shape)
m = np.ones(z.shape, dtype=bool)
for i in range(24):
z[m] = z[m] ** 2 + julia_C
m = np.abs(z) < 2
r += m
return r
def mandelbrot_set(x, y):
c = np.array(x + 1j * y)
z = np.zeros(c.shape, dtype=complex)
r = np.ones(c.shape)
m = np.ones(c.shape, dtype=bool)
for i in range(50):
z[m] = z[m] ** 2 + c[m]
m = np.abs(z) < 2
r += m
return r
def complex_str(c):
return np.array_str(np.array([julia_C]), suppress_small=True, precision=3)
def grid(width, offset, n):
x = np.linspace(-width + offset, width + offset,n)
y = np.linspace(-width, width, n)
return np.meshgrid(x,y), (x.min(), x.max(), y.min(), y.max())
fig, (ax, bx) = plt.subplots(1, 2)
ax.set_title("Mandelbrot Set(Mirror to Julia Set)")
bx.set_title("Julia Set c=" + complex_str(julia_C))
(X, Y), extent = grid(2, 0, 1000)
cf = ax.imshow(mandelbrot_set(X,Y), extent=extent)
(X, Y), extent = grid(2, 0, 1000)
julia = julia_set(X, Y)
img = bx.imshow(julia, extent=extent, cmap="gray")
def onclick(event):
if event.inaxes != ax: return
global X, Y, julia_C
julia_C = event.xdata + 1j * event.ydata
julia = julia_set(X, Y)
img.set_data(julia)
bx.set_title("Julia Set c=" + complex_str(julia_C))
fig.canvas.draw_idle()
fig.canvas.mpl_connect('button_press_event', onclick)
plt.tight_layout()
plt.show()