八大排序算法-及运行时间测试
以下测试及代码都用c实现
前言
不管是提高自身的能力,还是面试,八大排序都是很重要的一个知识点,所以理解并实践实现是很有必要的,以下给出算法思想与代码实现,并且进行运行时间测试八大排序的效率。
时间复杂度对比图
冒泡排序
冒泡排序是一种简单的排序算法。主要思想是顺序的比较相邻的两个数,如果符合比较条件就替换两个数,做法可以从后往前推,也可以从前往后推,每次推出当前长度的最大值,直至最后便可以完整的排序。
时间复杂度为 : O(n*n);
#include1]){
temp = arr[j];
arr[j] = arr[j-1];
arr[j-1] = temp;
}
}
}
}
//判断是否排序
bool isSorted(int arr[],int n){
bool flag = true;
for(int i=0;i1;++i){
if(arr[i+1]false;
break;
}
}
return flag;
}
int arr[N];
int main()
{
//随机播种
srand((unsigned)time(NULL));
for(int i =0;i < N;++i ){
arr[i] = rand()% MAX;
}
clock_t start_time=clock();
{
bubbleSort(arr,N);
}
clock_t end_time=clock();
printf("Running time is: %lfms\n",static_cast<double>(end_time-start_time)/CLOCKS_PER_SEC*1000);
printf("%s",isSorted(arr,N) == true ? "true":"false");
printf("\n");
return 0;
}
用10000个数进行测试:

运行时间为279ms
不要觉得很快这才一万的数据,再加两个0,就听几首歌慢慢等吧
冒泡有改进的方法是如果在比较相邻数的过程中都没交换过一次,说明后面的数已经排好序,可以直接跳出循环。
选择排序
思想:设当前位置为i,每次从i+1到n的数中选择最大(从大到小)或最小(从小到大)后,与位置i的值进行条件比较,符合条件则调换。
**时间复杂度为:**O(n*n)
#includeif(arr[j]if(index!=i){
temp = arr[i];
arr[i] = arr[index];
arr[index] = temp;
}
}
}
//判断是否排序
bool isSorted(int arr[],int n){
bool flag = true;
for(int i=0;i1;++i){
if(arr[i+1]false;
break;
}
}
return flag;
}
int arr[N];
int main()
{
srand((unsigned)time(NULL));
for(int i =0;i < N;++i ){
arr[i] = rand()% MAX;
}
clock_t start_time=clock();
{
chioseSort(arr,N);
}
clock_t end_time=clock();
printf("Running time is: %lfms\n",static_cast<double>(end_time-start_time)/CLOCKS_PER_SEC*1000);
printf("%s",isSorted(arr,N) == true ? "true":"false");
printf("\n");
return 0;
}
用10000个数进行测试:

运行时间为141ms
可以发现比冒泡速度更快点,主要原因是选择不需要每次都进行替换,只在最后一次再对比替换。
直接插入排序
思想:设当前位置为i,记录当前i的值为value,每次从i到0推,在推的过程中比较value的值,符合比较条件的值向后移,直至不符合条件时推结束,然后再将之前记录的value赋给不符和条件索引下标的后一个。
动画演示:
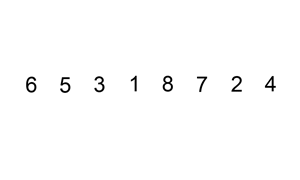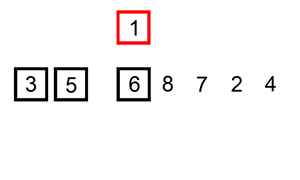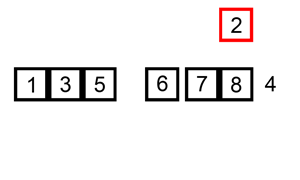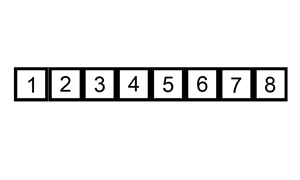
**时间复杂度:**O(n*n)
#include1;++i){
if(arr[i+1]false;
break;
}
}
return flag;
}
int arr[N];
int main()
{
srand((unsigned)time(NULL));
for(int i =0;i < N;++i ){
arr[i] = rand()% MAX;
}
clock_t start_time=clock();
{
// bubbleSort(arr,N);
// chioseSort(arr,N);
insertSort(arr,N);
}
clock_t end_time=clock();
printf("Running time is: %lfms\n",static_cast<double>(end_time-start_time)/CLOCKS_PER_SEC*1000);
printf("%s",isSorted(arr,N) == true ? "true":"false");
printf("\n");
return 0;
}
用10000个数进行测试:

用时75ms
可以发现比以上两种都快,原因主要是插入排序没有用到交换,而是直接赋值,交换两个数要3步,直接赋值只要1步,在数据的大情况下就差了2倍。
快速排序
思想:将一个复杂的问题划分为两部分,递归。每次在当前部分的数组中任取一个值value,重排数组(从小到大来说)将比value小的放左边,比value大的放右边,递归划分后得到的就是一个排完序的。
时间复杂度:O(n*logn);
特殊情况下(已经排好序的):O(n*n);
#includeif(arr[i]< value){
swap(&arr[index++],&arr[i]);
}
}
swap(&arr[index],&arr[end]);
return index;
}
void quickSort(int arr[],int start,int end){
if(end>start){
int index = partition(arr,start,end);
quickSort(arr, start,index-1);
quickSort(arr, index+1,end);
}
}
//判断是否排序
bool isSorted(int arr[],int n){
bool flag = true;
for(int i=0;i1;++i){
if(arr[i+1]false;
break;
}
}
return flag;
}
int arr[N];
int main()
{
srand((unsigned)time(NULL));
for(int i =0;i < N;++i ){
arr[i] = rand()% MAX;
}
clock_t start_time=clock();
{
quickSort(arr,0,N-1);
}
clock_t end_time=clock();
printf("Running time is: %lfms\n",static_cast<double>(end_time-start_time)/CLOCKS_PER_SEC*1000);
printf("%s",isSorted(arr,N) == true ? "true":"false");
printf("\n");
// for(int i=0;i
// printf("%d ",arr[i]);
// }
return 0;
} 
同样10000数据
只用了1ms
可知与以上的方法相比快了很多很多。
堆排序
二叉堆的定义
- 二叉堆是完全二叉树或者是近似完全二叉树。
- 二叉堆满足二个特性:
1.父结点的键值总是大于或等于(小于或等于)任何一个子节点的键值。
2.每个结点的左子树和右子树都是一个二叉堆(都是最大堆或最小堆)。
当父结点的键值总是大于或等于任何一个子节点的键值时为最大堆。当父结点的键值总是小于或等于任何一个子节点的键值时为最小堆。下图展示一个最小堆:

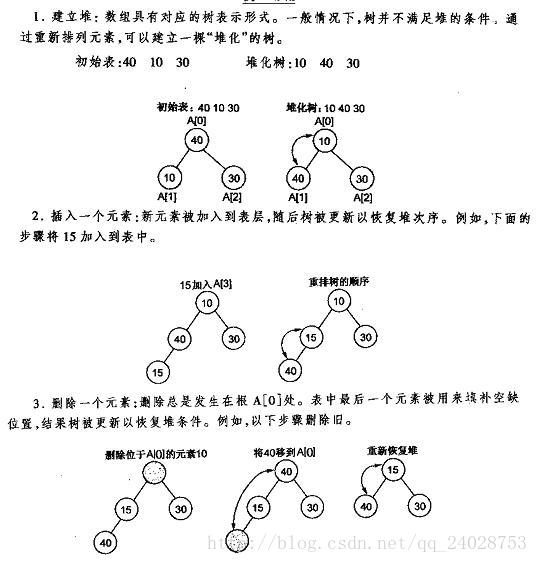
堆的存储
一般都用数组来表示堆,i结点的父结点下标就为(i – 1) / 2。它的左右子结点下标分别为2 * i + 1和2 * i + 2。如第0个结点左右子结点下标分别为1和2。
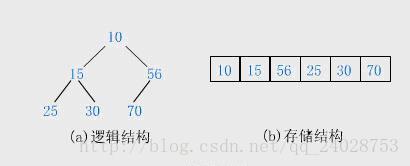
堆的操作——插入删除
堆的插入
每次插入都是将新数据放在数组最后。可以发现从这个新数据的父结点到根结点必然为一个有序的数列
// 新加入i结点 其父结点为(i - 1) / 2
void MinHeapFixup(int a[], int i)
{
int j, temp;
temp = a[i];
j = (i - 1) / 2; //父结点
while (j >= 0 && i != 0)
{
if (a[j] <= temp)
break;
a[i] = a[j]; //把较大的子结点往下移动,替换它的子结点
i = j;
j = (i - 1) / 2;
}
a[i] = temp;
} 更简短的表达为:
void MinHeapFixup(int a[], int i)
{
for (int j = (i - 1) / 2; (j >= 0 && i != 0)&& a[i] > a[j]; i = j, j = (i - 1) / 2)
Swap(a[i], a[j]);
} 堆的删除
按定义,堆中每次都只能删除第0个数据。为了便于重建堆,实际的操作是将最后一个数据的值赋给根结点,然后再从根结点开始进行一次从上向下的调整。调整时先在左右儿子结点中找最小的,如果父结点比这个最小的子结点还小说明不需要调整了,反之将父结点和它交换后再考虑后面的结点。相当于从根结点将一个数据的“下沉”过程。下面给出代码:
// 从i节点开始调整,n为节点总数 从0开始计算 i节点的子节点为 2*i+1, 2*i+2
void MinHeapFixdown(int a[], int i, int n)
{
int j, temp;
temp = a[i];
j = 2 * i + 1;
while (j < n)
{
if (j + 1 < n && a[j + 1] < a[j]) //在左右孩子中找最小的
j++;
if (a[j] >= temp)
break;
a[i] = a[j]; //把较小的子结点往上移动,替换它的父结点
i = j;
j = 2 * i + 1;
}
a[i] = temp;
}
//在最小堆中删除数
void MinHeapDeleteNumber(int a[], int n)
{
Swap(a[0], a[n - 1]);
MinHeapFixdown(a, 0, n - 1);
} 堆排序的两大步骤:
1. 建立初始化堆
2. 每次选取堆定元素进行排序
建立初始化堆
有了堆的插入和删除后,再考虑下如何对一个数据进行堆化操作。要一个一个的从数组中取出数据来建立堆吧,不用!先看一个数组,如下图:
![]()
很明显,对叶子结点来说,可以认为它已经是一个合法的堆了即20,60, 65, 4, 49都分别是一个合法的堆。只要从A[4]=50开始向下调整就可以了。然后再取A[3]=30,A[2] = 17,A[1] = 12,A[0] = 9分别作一次向下调整操作就可以了。下图展示了这些步骤:
![]()
写出堆化数组的代码:
// 从i节点开始调整,n为节点总数 从0开始计算 i节点的子节点为 2*i+1, 2*i+2
void MinHeapFixdown(int a[], int i, int n)
{
int j, temp;
temp = a[i];
j = 2 * i + 1;
while (j < n)
{
if (j + 1 < n && a[j + 1] < a[j]) //在左右孩子中找最小的
j++;
if (a[j] >= temp)
break;
a[i] = a[j]; //把较小的子结点往上移动,替换它的父结点
i = j;
j = 2 * i + 1;
}
a[i] = temp;
}
//建立最小堆
void MakeMinHeap(int a[], int n)
{
for (int i = n/ 2 -1 ; i >= 0; i--)
MinHeapFixdown(a, i, n);
} 每次选取堆定元素进行排序
首先可以看到堆建好之后堆中第0个数据是堆中最小的数据。取出这个数据再执行下堆的删除操作。这样堆中第0个数据又是堆中最小的数据,重复上述步骤直至堆中只有一个数据时就直接取出这个数据。
由于堆也是用数组模拟的,故堆化数组后,第一次将A[0]与A[n - 1]交换,再对A[0…n-2]重新恢复堆。第二次将A[0]与A[n – 2]交换,再对A[0…n - 3]重新恢复堆,重复这样的操作直到A[0]与A[1]交换。由于每次都是将最小的数据并入到后面的有序区间,故操作完成后整个数组就有序了。
void MinheapsortTodescendarray(int a[], int n)
{
for (int i = n - 1; i >= 1; i--)
{
Swap(a[i], a[0]);
MinHeapFixdown(a, 0, i);
}
} 注意使用最小堆排序后是递减数组,要得到递增数组,可以使用最大堆。
时间复杂度为:O(n*logn)
#include1;++i){
if(arr[i+1]false;
break;
}
}
return flag;
}
//----------------
//堆排序
//调整堆
void adjustHeap(int arr[],int index,int lenght){
int l = index*2+1;
int n = lenght;
int temp = arr[index];
while(lif((l+1)1]>arr[l])
l++;
if(arr[l] <= temp)
break;
arr[index] = arr[l];
index = l;
l = index*2+1;
}
arr[index] = temp;
}
//新建堆
void buildHeap(int arr[],int n){
for(int i = n/2 -1;i>=0;--i){
adjustHeap(arr,i,n);
}
}
void heapSort(int arr[],int n){
buildHeap(arr,n);
for(int i = n-1;i>0;--i){
swap(&arr[0],&arr[i]);
adjustHeap(arr,0,i);
}
}
//----------------------
int arr[N];
int main()
{
srand((unsigned)time(NULL));
for(int i =0;i < N;++i ){
arr[i] = rand()% MAX;
}
clock_t start_time=clock();
{
// bubbleSort(arr,N);
// chioseSort(arr,N);
//insertSort(arr,N);
// quickSort(arr,0,N-1);
heapSort(arr,N);
}
clock_t end_time=clock();
printf("Running time is: %lfms\n",static_cast<double>(end_time-start_time)/CLOCKS_PER_SEC*1000);
printf("%s",isSorted(arr,N) == true ? "true":"false");
printf("\n");
// for(int i=0;i
// printf("%d ",arr[i]);
// }
return 0;
}
可知在数据特别大的情况下堆排序的效率会比快排更好
希尔排序
略,笔者暂时没有研究希尔排序
归并排序
思想:所谓归并就是用了分治的算法思想(将一个大的问题划分为n个小问题,再用小问题得出的结果,解决大问题),主要思想就是将两个已经排好序的数组合并,最后这个数组就是有序的。
主要有两大步骤:
1. 先递归分解
2. 再递归合并
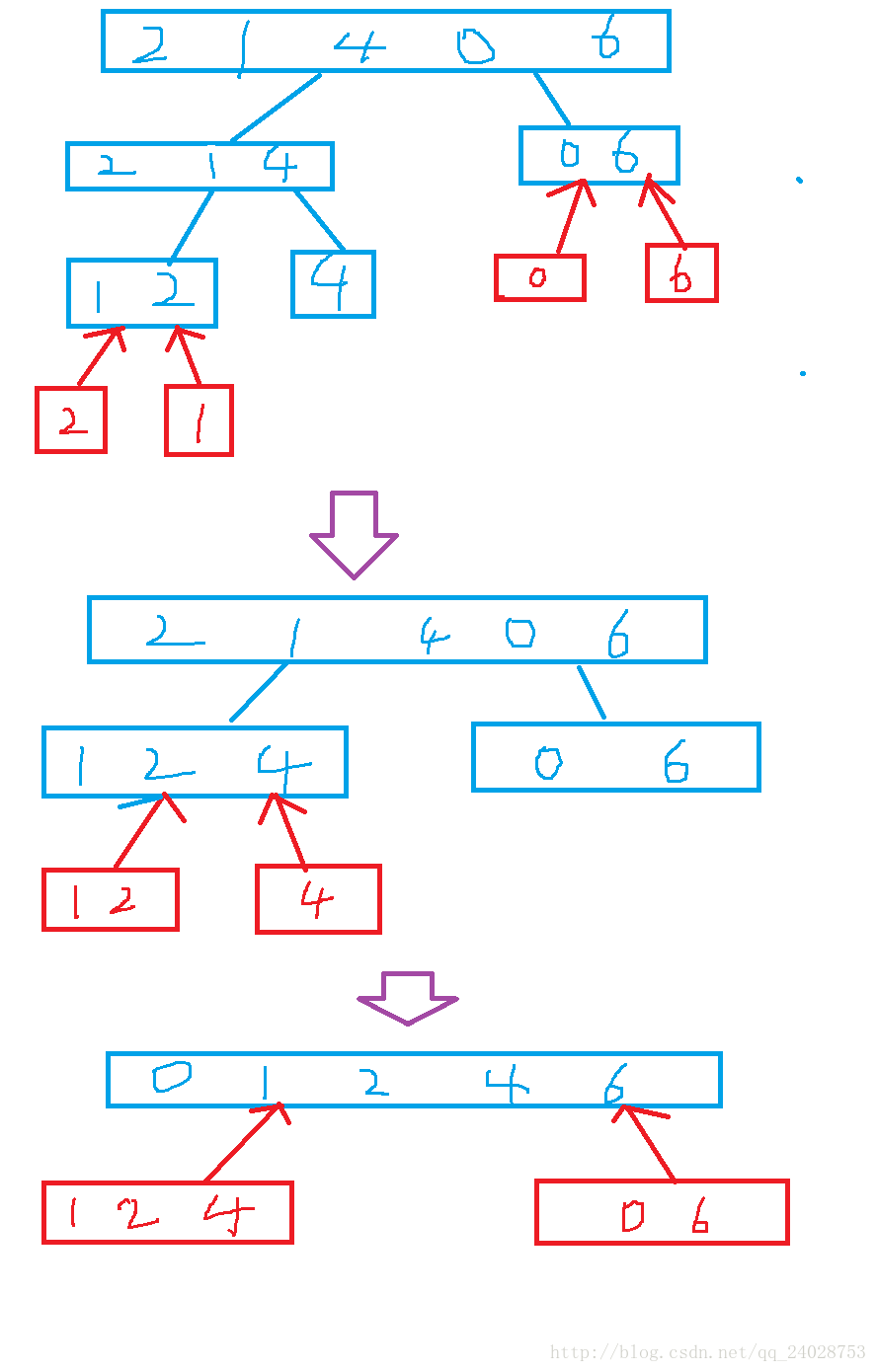
分解
一般采取二分的方法:将一个数组分为两部分,自顶向下分解

所以先了解下合并两数组:
将两个已经排好序的合并成一个排序数组
//辅助数组
int temp[N];
//-----------------------
void combineArr(int arrL[],int ln,int arrR[],int rn){
int i = 0;
int j = 0;
int k=0;
while(iif(arrL[i]<=arrR[j]){
temp[k++] = arrL[i++];
}else{
temp[k++] = arrR[j++];
}
}
while(iwhile(jfor(int i = 0;i 完整代码:
#includeif(arrL[i]<=arrR[j]){
temp[k++] = arrL[i++];
}else{
temp[k++] = arrR[j++];
}
}
while(iwhile(jfor(int i = 0;ivoid conflationSort(int arr[],int l,int r){
if(r>l){
int mid = (l+r)/2;
conflationSort(arr,l,mid);
conflationSort(arr,mid+1,r);
combineArr(&arr[l],mid-l+1,&arr[mid+1],r-mid);
}
}
//----------------------
int arr[N];
int main()
{
srand((unsigned)time(NULL));
for(int i =0;i < N;++i ){
arr[i] = rand()% MAX;
}
clock_t start_time=clock();
{
// bubbleSort(arr,N);
// chioseSort(arr,N);
//insertSort(arr,N);
// quickSort(arr,0,N-1);
//heapSort(arr,N);
conflationSort(arr,0,N-1);
}
clock_t end_time=clock();
printf("Running time is: %lfms\n",static_cast<double>(end_time-start_time)/CLOCKS_PER_SEC*1000);
printf("%s",isSorted(arr,N) == true ? "true":"false");
printf("\n");
// for(int i=0;i
// printf("%d ",arr[i]);
// }
return 0;
}
时间复杂度为:O(n*logn)
可知归并排序比快排,堆排序都快,并且稳定。
基数排序(桶排序)
基数排序是一种特殊的排序,它并不是通过比较数组中的数值进行排序,而是用了很特殊的方法:通过一个二维数组,每次根据进行位数入桶,最后按顺序遍历这二维数组,便可得出一个排好序的数组。
口诉太抽象了,下面用图解释:
时间近似复杂度为:O(n)
#includemaxN?arr[i]:maxN;
}
int exps = 1;
maxN = maxN/10;
while(maxN!=0){
maxN = maxN/10;
exps++;
}
return exps;
}
//基数排序
void radixSort(int arr[],int n){
//存每个桶中数的个数
int countIndex[10] = {0};
int exps = getMexExp(arr,n);
int exp = 1;
for(int e=0;e//入桶
for(int i=0;iint index = (arr[i]/exp)%10;
temps[index][countIndex[index]++] = arr[i];
}
//取值,改变数组
int k=0;
for(int i=0;i<10;++i){
//如果桶中数的个数大于0
if(countIndex[i]>0){
int n = countIndex[i];
//将数取出,改变数组
for(int j =0;j//将桶中的数的个数重置为0
for(int i=0;i<10;++i)
countIndex[i] = 0;
//位数改变
exp *=10;
}
}
//--------------------
int arr[N];
int main()
{
srand((unsigned)time(NULL));
for(int i =0;i < N;++i ){
arr[i] = rand()% MAX;
}
clock_t start_time=clock();
{
// bubbleSort(arr,N);
// chioseSort(arr,N);
//insertSort(arr,N);
// quickSort(arr,0,N-1);
//heapSort(arr,N);
// conflationSort(arr,0,N-1);
radixSort(arr,N);
}
clock_t end_time=clock();
printf("Running time is: %lfms\n",static_cast<double>(end_time-start_time)/CLOCKS_PER_SEC*1000);
printf("%s",isSorted(arr,N) == true ? "true":"false");
printf("\n");
// for(int i=0;i
// printf("%d ",arr[i]);
// }
return 0;
}

1000万数据,运行用时只用了941ms,
基数排序会占用比较大的空间,网上还有空间压缩的方法可参照:http://www.cnblogs.com/skywang12345/p/3603669.html
可知:基数排序的效率比以上所有排序速度都快(在数特别多的情况下,如果位数k,桶数10,k*10>n(数组个数),就不用基数排序了)
总结
参考文献: http://blog.csdn.net/morewindows/article/details/6709644/