题目描述
如图,A点有一个过河卒,需要走到目标B点。卒行走规则:可以向下、或者向右。同时在棋盘上的任一点有一个对方的马(如图中的C点),该马所在的点和所有跳跃一步可达的点称为对方马的控制点。例如图中C 点上的马可以控制9个点(图中的P1,P2...P8 和C)。卒不能通过对方马的控制点。
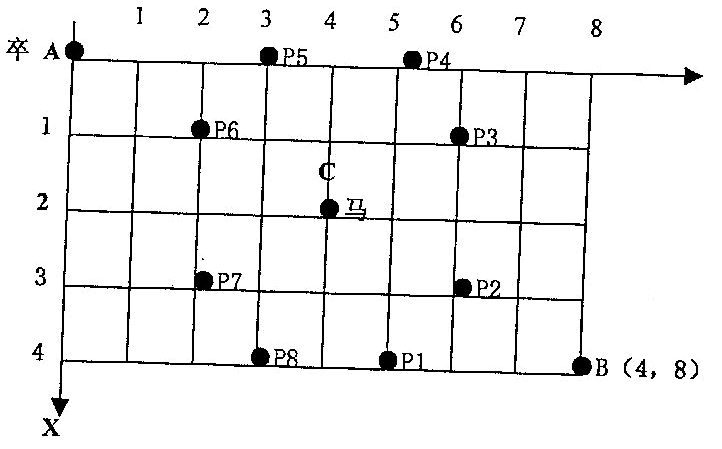
棋盘用坐标表示,A点(0,0)、B点(n,m)(n,m 为不超过20的整数,并由键盘输入),同样马的位置坐标是需要给出的(约定:C<>A,同时C<>B)。现在要求你计算出卒从A点能够到达B点的路径的条数。
输入
每个测试文件只包含一组测试数据,每组输入四个整数n,m,x,y。((n,m)表示B点的坐标,(x,y)表示对方马的坐标)
输出
对于每组输入数据,输出一个整数,表示路径的条数。
分析:到终点的路径是由之前的点一个一个递推来的,并且每到一个点,是不用管之前的状态是怎么来的,只需要用现在的状态又去不断递推后面的状态,那么其实也就满足了最优子结构,并且无后效性,那么也就想到了用DP来做,dp(i,j)表示从起点到(i,j)这个点的走法有多少种,然后把马本身和马的控制范围的点都打上标记,表明这些点不能走,将dp[0][0]赋初值为1,然后DP即可。。。其实这种问题很容易也可以想到用递归来做,但不能常规递归,因为中间重复计算了很多次,所以要用记忆化搜索。 注意数字较大,用long long 能过。
代码1 记忆化搜索:
#include
代码2 dp:
#include
