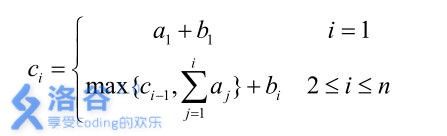寒假训练2018.2.2训练日志------贪心基础题目练习总结（二）

今天先对几个贪心的题目做下总结，然后开始学习动态规划的基础知识。

首先承接上次的国王奖励问题，总结本次的第一个问题：

一、P2123 皇后游戏

链接： https://www.luogu.org/problemnew/show/P2123

-------------------------------------------------------------------------------------------------------------------------------

题目描述

皇后有 n 位大臣，每位大臣的左右手上面分别写上了一个正整数。恰逢国庆

节来临，皇后决定为 n 位大臣颁发奖金，其中第 i 位大臣所获得的奖金数目为第

i－1 位大臣所获得奖金数目与前 i 位大臣左手上的数的和的较大值再加上第 i 位

大臣右手上的数。

形式化地讲：我们设第 i 位大臣左手上的正整数为 ai，右手上的正整数为 bi，

则第 i 位大臣获得的奖金数目为 ci可以表达为：

当然，吝啬的皇后并不希望太多的奖金被发给大臣，所以她想请你来重新安

排一下队伍的顺序，使得获得奖金最多的大臣，所获奖金数目尽可能的少。

注意：重新安排队伍并不意味着一定要打乱顺序，我们允许不改变任何一

位大臣的位置。

输入输出格式

输入格式：

第一行包含一个正整数 T，表示测试数据的组数。

接下来 T 个部分，每个部分的第一行包含一个正整数 n，表示大臣的数目。

每个部分接下来 n 行中，每行两个正整数，分别为 ai和 bi，含义如上文所述。

输出格式：

共 T 行，每行包含一个整数，表示获得奖金最多的大臣所获得的奖金数目。

输入输出样例

输入样例#1：  复制

1
3
4 1
2 2
1 2

输出样例#1：  复制

8

说明

对于全部测试数据满足： $T\le 10$  , $1\le n\le 20000$  , 1 \le a_i, b_i \le 10^91≤ai​,bi​≤109  。

--------------------------------------------------------------------------------------------------------------------------------------------------

与国王奖励问题相同，本题的关键在于归纳推理出排序条件，即使下一位大臣所获得的金币尽量少的排列策略。

推理分析：

       首先，通过题目给出的关于ci的分段函数表达式我们可以看出，排在后面的大臣所获得的金币数>=前一位大臣金币数，所以

现在假设有两种排列方式

第一次的错误分析：

a1	b1
a2	b2

a2	b2
a1	b1

易得ans1=max（a1+b1，a1+a2）+b2；ans2=max（a2+b2，a2+a1）+b1；

若假设ans1

错误在于考虑的只是第一位和第二位大臣的特殊情况，未考虑排在前面的大臣的金币数应是多少。

第二次分析改用  i 和  i+1  来表示两位大臣：

a[i]	b[i]
a[i+1]	b[i+1]

a[i+1]	b[i+1]
a[i]	b[i]

首先，我们假设前i-1项已经排序完毕，且前i-1为大臣右手数字和为sum，第i-1位大臣所得金币数为x；

则得ans1=max（max（x，sum+a[i]）+b[i]，a[i+1]+a[i]+sum）+b[i+1]；

同理ans2=max（max（x，sum+a[i+1]）+b[i+1]，a[i]+a[i+1]+sum）+b[i]；

将所有项均放入max中（理由见下面）得：

ans1=max（x+b[i]+b[i+1]，sum+a[i]+b[i]+b[i+1]，a[i+1]+a[i]+sum+b[i+1]）；

ans2=max（x+b[i]+b[i+1]，sum+a[i+1]+b[i+1]+b[i]，a[i]+a[i+1]+sum+b[i]）；

下面注意：当所有元素均在一个max中时，对于相同的元素可舍去：

--------------------------------------------------------------------------------------------------------------------------------------------------

理由（做个小证明，虽然很简单）：以简单不等式max（a，1）

①a1成立，b>1成立，即1

②a<1：此时a>1成立，显然不成立，舍去；

③11成立，即a<1

④1<1：显然不成立，舍去。

综上所述：原式若成立，则必有   a

同时可以看出，若原式两边有额外的不相等的常数：如   max（a，1）

①a1成立，b>1成立，即11；

②a<1+c：此时a>1成立，b<1成立，即b<1

③11成立，即a<1

④1<1+c：c>0；

显然，我们得不到一个绝对成立的结论，即找不到原式的一个等价式。

--------------------------------------------------------------------------------------------------------------------------------------------------

继续分析，去掉相同项后得到：

ans1=max（sum+a[i]+b[i]+b[i+1]，a[i+1]+a[i]+sum+b[i+1]）；

ans2=max（sum+a[i+1]+b[i+1]+b[i]，a[i]+a[i+1]+sum+b[i]）；

同理约掉sum得：

ans1=max（a[i]+b[i]+b[i+1]，a[i+1]+a[i]+b[i+1]）；

ans2=max（a[i+1]+b[i+1]+b[i]，a[i]+a[i+1]+b[i]）；

其实到这一步，我们的排序规则已经出来了，只是形式麻烦点，若ans1

max（a[i]+b[i]+b[i+1]，a[i+1]+a[i]+b[i+1]）<max（a[i+1]+b[i+1]+b[i]，a[i]+a[i+1]+b[i]）排序，

若进一步化简：可同时减去a[i]+b[i]+b[i+1]+a[i+1]，得到：  max（-a[i+1]，-b[i]）

提出负号得：min（a[i+1]，b[i])>min（a[i]，b[i+1]）。

AC代码：略

---------------------------------------------------------------------------------------------------------------------------------

 二、P1233 木棍加工

题目链接： https://www.luogu.org/problemnew/show/P1233

题目描述

一堆木头棍子共有n根，每根棍子的长度和宽度都是已知的。棍子可以被一台机器一个接一个地加工。机器处理一根棍子之前需要准备时间。准备时间是这样定义的：

第一根棍子的准备时间为1分钟；

如果刚处理完长度为L，宽度为W的棍子，那么如果下一个棍子长度为Li，宽度为Wi，并且满足L>＝Li，W>＝Wi，这个棍子就不需要准备时间，否则需要1分钟的准备时间；

计算处理完n根棍子所需要的最短准备时间。比如，你有5根棍子，长度和宽度分别为(4, 9)，(5, 2)，(2, 1)，(3, 5)，(1, 4)，最短准备时间为2（按(4, 9)、(3, 5)、(1, 4)、(5, 2)、(2, 1)的次序进行加工）。

输入输出格式

输入格式：

第一行是一个整数n(n<＝5000)，第2行是2n个整数，分别是L1，W1，L2，w2，…，Ln，Wn。L和W的值均不超过10000，相邻两数之间用空格分开。

输出格式：

仅一行，一个整数，所需要的最短准备时间。

输入输出样例

输入样例#1：  复制

5
4 9 5 2 2 1 3 5 1 4

输出样例#1：  复制

2

---------------------------------------------------------------------------------------------------------------------------------

与导弹拦截题目类似，增加的一分钟可以看作增加了一台机器。

*（补充：与导弹拦截不同的是这里的木头有两个参数，而导弹只有一个参数，所以我们把长度按降序排列，使后面的木头在长度上均满足条件，从而只考虑宽度（把长度比作导弹威力，威力在不断减小，前面的各套系统均有拦截之后所有导弹的威力，也就无所谓谁拦截会使系统数最少），剩下的就和导弹问题完全一样了，处理一堆无序数列。）

所以思路：

       结构体记录长与宽，先降序排序（贪心，本题长或宽做排序条件均可，以长为例），之后两层循环，一个for扫描数据，一个for枚举已有机器，将当前数据分别与每台机器记录的数据对比，记录最先符合条件的机器号码，之后若再有符合的机器，将该机器记录数据与前一次记录机器号的数据比较，取较小者机器号作为新的记录，机器枚举完毕，判断是否记录过机器号，若记录过，更新该机器的数据；否则，加一台机器，并记录数据。继续第一个for的执行直至扫描完毕，输出结果。

AC代码：

#include
using namespace std;
struct wood
{
    int l,w;
}a[5001],b[5001];//a储存木头，b储存各台机器（多用时间）
bool complare(wood x,wood y)
{
    if(x.l==y.l)return x.w>y.w;
    return x.l>y.l;
}
int main()
{
    int n;cin>>n;
    for(int i=1;i<=n;++i)cin>>a[i].l>>a[i].w;
    sort(a+1,a+1+n,complare);

    int k=1;
    b[1].w=a[1].w;
    int x,y;
    for(int i=2;i<=n;++i)
    {
        int p=0;
        for(int j=1;j<=k;++j)
        {
            if(b[j].w>=a[i].w)
            {
                if(p==0)p=j;
                else if(b[j].w

---------------------------------------------------------------------------------------------------------------------------------

 三、P1315 观光公交

 链接：https://www.luogu.org/problemnew/show/P1315