贪婪算法(greedy Algorithm)
贪婪算法的应用:
相关算法练习题:
LeetCode股票买卖的最佳时机
LeetCode判断子序列
LeetCode 分发饼干
LeetCode跳跃游戏
LeetCode加油站
一、简单调度问题:
给出作业和作业的运行时间,现在只有一个处理器,我们假设使用非预占调度(一旦开始一个作业,必须完成),现在我们要把作业平均完成的时间最小化。
举例:
| 作业 | 时间 |
|---|---|
| j1 | 15 |
| j2 | 8 |
| j3 | 3 |
| j4 | 10 |
其中一种调度方式:
| 15 | 8 | 3 | 10 |
|---|---|---|---|
| j1 | j2 | j3 | j4 |
完成作业花费的时间:
j1=15
j2=15+8=23
j3=15+8+3=26
j4=15+8+3+10=36
一共花费的时间:
15+23+26+36=100
15×4+8×3+3×2+10×1
所以,平均完成一项作业需要:
100/4=25;
如何使平均完成时间最少?
j1是第一个完成的作业, 则它所花的时间一共要累加 4次
j2 是第二个完成的作业,则它所花的时间一共要累加 3次
出现 第 i 次,累加 (n-i+1)次
该调度花的总时间:

要使总花的时间最少,C的前面一个求和公式是固定的,后面一个求和要最大。显然,当 K大的时候,tk是大的,则这样累加起来最大。
举个例子:
k=0,1,t1=23,t2=7
0×7+23×1=23 > 1×7+23×0=7
所以,时间花费少的要在前面完成,时间花费多的要在后面完成。这个结果也指出了为什么操作系统要将优先级给短的程序。
根据上述描述的方法我们做出另一种调度方式:
| 3 | 8 | 10 | 15 |
|---|---|---|---|
| j3 | j2 | j4 | j1 |
平均完成一项是17.5,明显该种调度方式就是最优调度。
扩展:
当多处理器时,按顺序开始作业,多处理器交叉处理。
如果要求的是这些作业的最早结束时间,则这个问题便是NP-完全的。实际上,所有的调度问题要么NP-完全的,要么是贪婪可解的。
二、应用处理文件压缩
假设我们有7个字符,每个字符出现的频率不等。
| a | c | e | g | w | t | i |
|---|---|---|---|---|---|---|
| 45 | 3 | 21 | 8 | 10 | 30 | 80 |
如果我们按照一般的方法来存储这些数据,那么我们应该用3位二进制码来表示这7个字符。
因此我们一共要存储数据总量:
Σ(3×出现的频率)
这样出现频率低的编码和出现频率高的编码都是一样的长度,如果我们要使它的数据总量尽可能地少,那么我们想出了另外一种方法来表示编码,使得出现频率越高则编码越短,这种编码就叫做Huffman编码。
如何构造一个Huffman编码呢,我们在二叉树的帮助下。
我们令这些字符作为一个树的叶子结点,
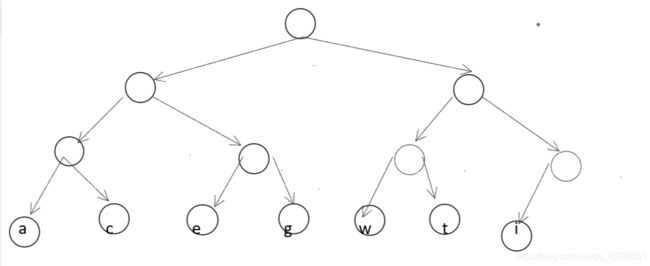
从根结点开始,左边分支上的权0,右边上为1。那么每个字符都有一个编码。
现在我们对树进行修改,使它成为一颗Huffman树,Huffman树是满足下列三个条件的树:
- 字符只能够在叶子结点上,这样规定是为了防止一个字符是另一个字符的前缀编码,防止造成二义性。
比如在 t 的父节点是字符 b ,那么 t:101;b:10,当我们有个编码串为 101001001 则首个字符可以解释为t 也可以为 b。 - 我们可以把 i 向上移动一层,这是没有影响的。
- 出现频率最大的字符所在的叶子结点要尽量在上层,这样它的编码长度才会尽可能短。
如何构造Huffman 树?
1.为所有字符创建叶子结点,并且把这些结点全部放在最小堆里
2.从最小堆里找出两个出现频率最小的叶子
3.创建一个新的内部结点,新的内部节点的频率是第二步里找出来的两个结点的和,两个结点一个作为内部结点的左结点,一个作为内部结点的右结点,然后将新的内部结点添加到最小堆里,而两个结点去除
4.重复上述2,3,直到最小堆里直剩下一个结点,剩下的结点是树的根节点,到此为止,Huffman tree 形成!
这个算法是贪婪算法的原因是我们每次只选取两个最小的叶子 结点,而没有进行全局的考虑。
三、近似装箱问题
当我们解决问题时,为了找到全局最优解,我们通过在每个步骤寻找局部最优,但是有时我们不能够获得全局最优。
greedy:1+3+7=11
actual:1+2+4+8+12=27
因此,局部最优解不一定会得到全局最优解。
那什么时候可以使用贪婪算法呢?
满足两个条件:
1.全局最优可以由局部最优得到,但是这个只有在我们得出结果后才能知道是不是最优的。
2.最优子结构:
an optimal solution to the problem contains an optimal solution to subproblems
这里和动态规划的区别,贪心算法从来不会再重新考虑他的选择
我们将使用一些方法使得所得的解离最优解不是很远。
装箱问题一般分为两种:
- 联机装箱(on-line):
必须将一个物品放到一个箱子里,才能处理下一个物品。来一个我装一个 - 脱机装箱(off-line)
只有当输入数据全部输入才能进行工作。所有物品都来了,我再一起装
联机装箱
1.下项合适(next fit)算法
当处理一个物品时我们看它可以不可以装进刚刚装进物品的箱子里,如果可以,则装入;如果不可以,则新开辟一个箱子。
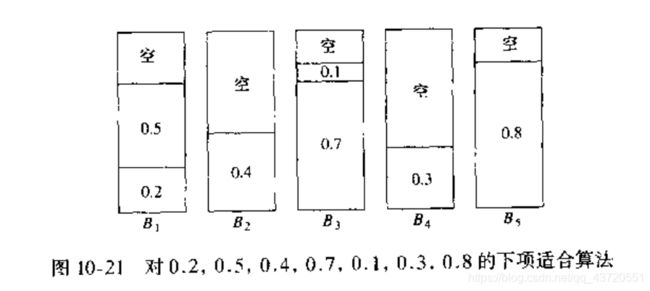
算法改进:0.3其实不用新开辟箱子,而可以放在B2中,因此我们引入第二种算法。
2.首次合适(first fit)算法
当处理一个物品时,我们同时遍历所以的箱子,将物品放在第一个可以容纳物品的箱子中。

算法改进:0.3也许我们可以将它放在B3,这样虽然没有使箱子的个数减少,但是,如果还有新的物品进来,更能容纳更多的物品,于是我们引入最优合适算法。
3.最优合适(best fit)算法
当处理一个新的物品时,同时遍历箱子,使得物品放在使得箱子最满的情况下。
综上,我们发现了,联机算法最大的弊端就是大项物品装箱困难,尤其是当大项物品是后面处理的,这样我们要不停的开辟新的箱子,因此,如果我们先将大项物品放入箱子中,这样是不是更好呢?于是我们引入脱机算法。
脱机装箱
当所有物品都已经给出,我们先对它们进行排序,将大的物品先进行装箱。此时我们可以运用联机算法的首次适合算法和最优适合算法,此时称为首次适合非增算法和最优适合非增算法。
应用
1.Activity Selection Problem
给了一些活动的开始时间和结束时间,对于一个人来说,他最多可以完成多少活动
方法:
1.我们先通过结束时间对活动进行排序
2.选择第一个活动。
3.然后遍历剩下的活动,如果剩下的活动开始时间晚于或等于他的前一个活动的结束时间,则可以选择这个活动,否则不行
2.Huffman coding
3.Job Sequencing Problem
4.Fractional Knapsack Problem
5.Prim’s Minimum Spanning Tree
未完待续。
