模式匹配算法

串运算的概念浅析

模式匹配：子串的定位操作被叫做串的模式匹配。

串大小的比较：

串相等：串长度相等且各个对应位置的字符都相等。
当两个串不相等时，判断两个串大小的方法：
给定两个串：S1 = “a1a2a3a4…an”和S2 = “b1b2b3b4…bm”，当满足以下条件之一时，S1

1. n
2. 存在某个k<=min(m,n), 使得ai=bi(i = 1,2,3,…k-1),ak

Brute-Force算法

一种最简单粗暴的模式匹配算法，目的是为了寻找模式串T是否在目标串S中有出现。
思想：先从主串第i个字符开始匹配，如果T[j]==S[i]，那么继续向下比较，一旦不相等，即回溯到目标串的下一个字符即(i = i-j+2)，重复工作。

成功条件：当循环结束时，判断j的值与模式串p的长度是否相等，如果相等，说明匹配成功到了模式p的最后一个字符。

返回值：失败返回0，成功返回模式串在目标串中出现的位置。

int bf(char *mother_string, char *son_string, int position)
{
    size_t i = position;
    size_t j = 1;                                                                                                                                             
    while (i <= strlen(mother_string) && j <= strlen(son_string)) {
        if (mother_string[i] == son_string[j]) {
            i++;
            j++;
        } else {
            i = i - j + 2;
            j = 1;
        }   
    }   
    if (j == strlen(son_string) + 1) {
        return i - strlen(son_string);
    } else {
        return 0;
    }   
}

KMP算法

因为BF算法的过于低效，所以诞生了KMP算法。
KMP模式匹配算法的原理：

#define SIZE_NEXT 225

void get_kmp_next(char *string, int *next)
{
    size_t i = 1;
    int j = 0;
    next[1] = 0;
    while (i < strlen(string)) {
        if (j == 0 || string[i] == string[j]) {
            i++;
            j++;
            next[i] = j;//更新模式串string每个位置上对应的位置变化
        } else {
            j = next[j];//回溯j值
        }
    }
}

// next[j] = x意味着重新开始比的时候，对于模式串string来说前x-1个不用比较，肯定是相同的，只需要从第x个开始即可

int kmp(char *mother_string, char *son_string, int position)
{
    size_t i = position, j = 1;
    int *next = (int *)malloc(SIZE_NEXT*sizeof(int));
    get_kmp_next(son_string, next);
    while (i < strlen(mother_string) && j < strlen(son_string)) {
        if (j == 0 || mother_string[i] == son_string[j]) {// j == 0意味着第一个字符就不相同 如果j != 0 且不相等那么else更新j的位置。
            i++;
            j++;
        } else {
            j = next[j];
        }
            }
    if (j == strlen(son_string) + 1) {
        return i-strlen(son_string);
    } else {
        return 0;
    }
}

KMP算法的改进

如果目标穿为aaaabcde
模式串为aaaaax,那么模式串的next数组值分别为012345
按照上面的KMP算法，我们将会得到以下的过程
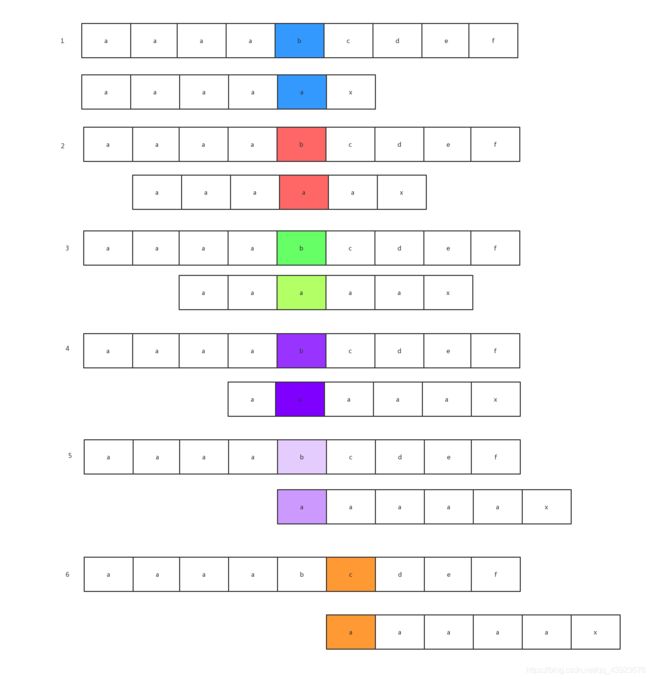但我们会发现，2,3,4,5步完全是多余的判断，由于模式串的2,3,4,5位置的字符都与1位置的相等，那么我们就可以用1位的next数组值去取代与它相等的字符后续next[j]的值，我们将取代next数组的数组命名为nextval数组。

void get_kmp_nextval(char *string, int *nextval)                          
{                                                                   
    size_t i = 1;                                                   
    int j = 0;                                                      
    nextval[1] = 0;                                                    
    while (i < strlen(string)) {                                    
        if (j == 0 || string[i] == string[j]) {                     
            i++;                                                    
            j++;                           
            if (string[i] != string[j]) { 
                nextval[i] = j;
            } else { 
                nextval[i] = nextval[j];                                                                                                                      
            }
        } else {        
            j = nextval[j];
        }                                                           
    }                                                               
}