HNUCM2020年春季ACM集训队热身赛-第6场题解

问题 A: 最小素数对

题目描述

任意一个偶数（大于2）都可以由2个素数组成，组成偶数的2个素数有很多种情况，本题目要求输出组成指定偶数的两个素数差值最小的素数对。

输入

输入一个偶数。

输出

输出两个素数。

样例输入

20

样例输出

7
13

数据不大，直接枚举所有情况，判断两个数是不是素数即可

#include 
#define ll long long
using namespace std;
const int maxn=1e5+5;
bool ju(int x){
    for(int i=2;i*i<=x;++i){
        if(x%i==0)return false;
    }
    return true;
}
int main()
{
    int n,ans1,ans2;
    scanf("%d",&n);
    for(int i=2;i<=n/2;++i){
        if(ju(i)&&ju(n-i)){
            ans1=i,ans2=n-i;
        }
    }
    printf("%d\n%d\n",ans1,ans2);
    return 0;
}

---

问题 B: 自守数

题目描述

自守数是指一个数的平方的尾数等于该数自身的自然数。例如：25^2 = 625，76^2 = 5776，9376^2 = 87909376。请求出n以内的自守数的个数。

输入

int型整数。

输出

n以内自守数的数量。

样例输入

2000

样例输出

8

暴力跑出所有自守数，在对输入的数进行判断

暴力代码

#include 
#define ll long long
using namespace std;
const int maxn=1e5+5;
bool ju(ll x){
    ll y=x*x;
    while(x>0&&y>0){
        if(x%10!=y%10)return false;
        x/=10,y/=10;
    }
    return true;
}
int main()
{
    ll n;
    int ans=0;
    scanf("%lld",&n);
    for(int i=0;i<=n;++i){
        if(ju(i)){
            ++ans;
        }
    }
    printf("%d",ans);
    return 0;
}

提交代码

#include 
using namespace std;
#define long long ll;
int main(){
    int n,ans=0;
    int a[18]={0,1,5,6,25,76,376,625,9376,90625,109376,890625,2890625,7109376,12890625,87109376,212890625,787109376};
    scanf("%d",&n);
    for(int i=0;i<18;++i){
        if(n>=a[i])++ans;
        else break;
    }
    printf("%d\n",ans);
    return 0;
}

---

问题 C: 埃及分数

题目描述

分子为1的分数称为埃及分数。现输入一个真分数(分子比分母小的分数，叫做真分数)，请将该分数分解为埃及分数。如：8/11 = 1/2+1/5+1/55+1/110。 但这次我们不需要输出满足埃及分数的分解^_，输出任意一种正确分法即可

输入

输入一个真分数（字符串）。

输出

输出分解后的埃及分数（字符串）。

样例输入

8/11

样例输出

1/2+1/5+1/55+1/110

输出任意解即可
a/b可以分成a个1/b

#include 
#define ll long long
using namespace std;
const int maxn=1e5+5;
int main()
{
    int a,b;
    scanf("%d/%d",&a,&b);
    for(int i=1;i<=a;++i){
        printf("1/%d%c",b,i==a?'\n':'+');
    }
    return 0;
}

---

问题 D: 字典序

题目描述

给定n个字符串，请对n个字符串按照字典序排列。

输入

输入第一行为一个正整数n(1≤n≤1000),下面n行为n个字符串(字符串长度≤100),字符串中只含有大小写字母。

输出

数据输出n行，输出结果为按照字典序排列的字符串。

样例输入

9
cap
to
cat
card
two
too
up
boat
boot

样例输出

boat
boot
cap
card
cat
to
too
two
up

string存字符串sort排序

#include 
#define ll long long
using namespace std;
const int maxn=1e5+5;
string a[1005];
int main()
{
    int n;
    cin>>n;
    for(int i=1;i<=n;++i)cin>>a[i];
    sort(a+1,a+n+1);
    for(int i=1;i<=n;++i)cout<<a[i]<<endl;
    return 0;
}

---

问题 E: 1的个数

题目描述

输入一个int型的正整数，计算出该int型数据在内存中存储时1的个数。

输入

输入一个整数（int类型）。

输出

这个数转换成2进制后，输出1的个数。

样例输入

5

样例输出

2

#include 
#define ll long long
using namespace std;
const int maxn=1e5+5;
int main()
{
    int n,ans=0;
    scanf("%d",&n);
    while(n){
        if(n&1)++ans;
        n>>=1;
    }
    printf("%d\n",ans);
    return 0;
}

---

问题 F: 数字整除

题目描述

定理：把一个至少两位的正整数的个位数字去掉，再从余下的数中减去个位数的5倍。当且仅当差是17的倍数时，原数也是17的倍数 。

例如，34是17的倍数，因为3-20=-17是17的倍数；201不是17的倍数，因为20-5=15不是17的倍数。输入一个正整数n，你的任务是判断它是否是17的倍数。

输入

输入文件最多包含10组测试数据，每个数据占一行，仅包含一个正整数n（1<=n<=10100），表示待判断的正整数。n=0表示输入结束，你的程序不应当处理这一行。

输出

对于每组测试数据，输出一行，表示相应的n是否是17的倍数。1表示是，0表示否。

样例输入

34
201
2098765413
1717171717171717171717171717171717171717171717171718
0

样例输出

1
0
1
0

题面介绍了一个定理，但是感觉问题变得更麻烦了
那就不管它，直接判断是否可以被17整除
用数组存n，模拟除法

#include 
#define ll long long
using namespace std;
const int maxn = 2e5+5;
const int inf = 0x3f3f3f3f;
char s[maxn];
int main(){
    int n;
    while(~scanf("%s",&s)){
        if(strcmp(s,"0")==0){
            break;
        }
        int ls=strlen(s),ans=0;
        for(int i=0;i<ls;++i){
            ans=ans*10+(s[i]-'0');
            ans%=17;
        }
        ans%=17;
        if(ans==0){
            printf("1\n");
        }else{
            printf("0\n");
        }
    }
}

---

问题 G: 多连块拼图

题目描述

多连块是指由多个等大正方形边与边连接而成的平面连通图形。
– 维基百科

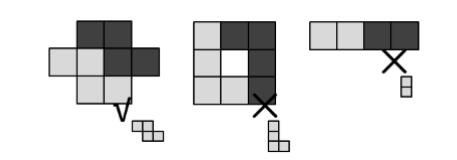
给一个大多连块和小多连块，你的任务是判断大多连块是否可以由两个这样的小多连块拼成。小多连块只 能平移，不能旋转或者翻转。两个小多连块不得重叠。左下图是一个合法的拼法，但右边两幅图都非法。中间 那幅图的问题在于其中一个小多连块旋转了，而右图更离谱：拼在一起的那两个多连块根本就不是那个给定的 小多连块（给定的小多连块画在右下方）。

输入

输入最多包含 20 组测试数据。每组数据第一行为两个整数 n 和 m(1<=m<=n<=10)。以下 n 行描述大多连 块，其中每行恰好包含 n 个字符或者.，其中表示属于多连块，.表示不属于。以下 m行为小多连块，格式同大 多连块。输入保证是合法的多连块（注意，多连块至少包含一个正方形）。输入结束标志为 n=m=0。

输出

对于每组测试数据，如果可以拼成，输出 1，否则输出 0。

样例输入

4 3
.**.
****
.**.
....
**.
.**
...
3 3
***
*.*
***
*..
*..
**.
4 2
****
....
....
....
*.
*.
0 0

样例输出

1
0
0

每一次匹配找到a的第一个星号和b的第一个星号，找到映射关系，进行匹配
匹配失败直接输出0
匹配两次后还有*也输出0

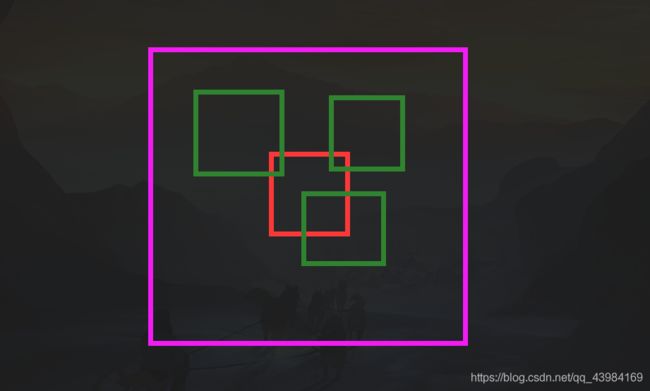
避免一些数据使下标访问越界如

3 3
*..
...
...
...
...
..*

所以将数组开成30（紫红色框），横纵坐标全部加10
那数组b（绿色框）在数组a（红色框）匹配的时候就不会越界

#include 
#include 
#include 
#include 
#include 
#include 
#include 
#include 
#include 
#define ll long long
using namespace std;
const int inf = 0x3f3f3f3f;
const int maxn = 1e7 + 5;
char a[35][35],b[35][35];
int n,m;
struct node{
    int x,y;
};
node get(char s[35][35],int x){//获得数组s第一个*的坐标
    node ans;
    ans.x=ans.y=0;
    for(int i=11;i<=x+10;++i){
        for(int j=11;j<=x+10;++j){
            if(s[i][j]=='*'){
                ans.x=i,ans.y=j;
                return ans;
            }
        }
    }
    return ans;
}
bool solve(){//对a和b进行一次匹配，匹配失败返回false
    node p=get(a,n),q=get(b,m);
    if(p.x==0)return true;
    int xx=p.x-q.x+1,yy=p.y-q.y+1;//a中的点(xx,yy)对应   b中的点(1,1)
    for(int x=11;x<=m+10;++x){
        for(int y=11;y<=m+10;++y){
            if(a[xx+x-1][yy+y-1]!='*'&&b[x][y]=='*'){//b有a没有，匹配失败
                return false;
            }else if(a[xx+x-1][yy+y-1]=='*'&&b[x][y]=='*'){
                a[xx+x-1][yy+y-1]='.';
            }
        }
    }
    return true;
}
int main()
{
    while(~scanf("%d %d",&n,&m)&&(n||m)){
        for(int i=11;i<=n+10;++i)scanf("%s",a[i]+11);
        for(int i=11;i<=m+10;++i)scanf("%s",b[i]+11);
        if(solve()==false){
            printf("0\n");
            continue;
        }
        if(solve()==false){
            printf("0\n");
            continue;
        }
        if(get(a,n).x==0){//a中没有*号
            printf("1\n");
        }else{
            printf("0\n");
        }
    }
    return 0;
}

---

问题 H: 最优对称路径

题目描述

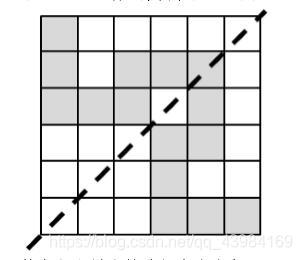
给一个 n 行 n 列的网格，每个格子里有一个 1 到 9 的数字。你需要从左上角走到右下角，其中每一步只能 往上、下、左、右四个方向之一走到相邻格子，不能斜着走，也不能走出网格，但可以重复经过一个格子。为 了美观，你经过的路径还必须关于“左下-右上”这条对角线对称。下图是一个 6x6网格上的对称路径。

你的任务是统计所有合法路径中，数字之和最小的路径有多少条。

输入

输入最多包含 25组测试数据。每组数据第一行为一个整数 n（2<=n<=100）。以下 n 行每行包含 n 个 1 到 9 的数字，表示输入网格。输入结束标志为 n=0。

输出

对于每组数据，输出合法路径中，数字之和最小的路径条数除以 1,000,000,009 的余数。

样例输入

2
1 1
1 1
3
1 1 1
1 1 1
2 1 1
0

样例输出

2
3

路径是对称的，我们找到了一边的路径另一边的路径也就确定
将网格按左下到右上的对角线折叠，右下的数字加到左上，从点（1，1）走到对角线就确定了一条路径

对于最优路径数量
先bfs处理出从（1，1）开始到每一个格子的最少数字和。
获得到对角线的最小数字和后，dfs计算路径数量
避免超时，也要进行剪纸和记忆化

#include 
#define ll long long
using namespace std;
const int inf = 0x3f3f3f3f;
const int maxn = 1e7 + 5;
const int mod = 1000000009;
int n,a[205][205],ans[205][205],vis[205][205];
int dis[205][205],minn;
int dir[4][2]={1,0,-1,0,0,1,0,-1};
struct node{int x,y;};
bool ju(node x){//判断是否越界
    if(x.x>=1&&x.x<=n&&x.y>=1&&x.y<=n)return true;
    return false;
}
void bfs(){
    queue<node > pq;
    node now,ne;
    now.x=1,now.y=1;
    pq.push(now);
    memset(dis,inf,sizeof(dis));
    dis[1][1]=a[1][1];
    while(!pq.empty()){
        now=pq.front(),pq.pop();
        if(now.x+now.y==n+1){//到对角线，维护最小值
            minn=min(minn,dis[now.x][now.y]);
            continue;
        }
        for(int i=0;i<4;++i){
            ne.x=now.x+dir[i][0];
            ne.y=now.y+dir[i][1];
            if(ju(ne)&&dis[ne.x][ne.y]>dis[now.x][now.y]+a[ne.x][ne.y]){
                dis[ne.x][ne.y]=dis[now.x][now.y]+a[ne.x][ne.y];
                pq.push(ne);
            }
        }   
    }
}
ll dfs(int x,int y){
    if(ans[x][y]!=-1)return ans[x][y];//记忆化
    if(x+y==n+1){
        ans[x][y]=(dis[x][y]==minn);
        return ans[x][y];
    }
    ans[x][y]=0;
    for(int i=0;i<4;++i){
        int xx=x+dir[i][0];
        int yy=y+dir[i][1];
        if(dis[xx][yy]==dis[x][y]+a[xx][yy]){//剪枝，每一次都按最优路径走
            ans[x][y]+=dfs(xx,yy);
            ans[x][y]%=mod;
        }
    }
    return ans[x][y]%mod;
}
int main()
{
    while (~scanf("%d", &n) && n)
    {
        minn=inf;
        for(int i=1;i<=n;++i)
            for(int j=1;j<=n;++j){
                scanf("%d",&a[i][j]);
                if(i+j>n+1)
                    a[n-j+1][n-i+1]+=a[i][j];
            }
        bfs();
        memset(ans,-1,sizeof(ans));
        printf("%lld\n",dfs(1,1));
    }
    return 0;
}