【Day4】【纪中OJ】2019.1.26大型被虐C组模拟赛（游记+题解）

---

游记

Morning

【Before 8:00】依然起得很晚，以至没有早餐吃了555。在洛谷打了卡，大吉（请一定要记住这个大吉）。然后发现今天的比赛竟然7:40就开始了。。。
【Before 10:00】今天C组的题目依然很难。

题目	做法
连续自然数和	暴力枚举
简(he)单(bing)游(guo)戏(zi)	DFS+剪枝
幸运票	递推+高精
抄书	二分

【Before 11:00】 OJ被卡爆了！2个小时！大家都无心做题，都在FB！！！
【Before 12:00】 分数出来了。
得分:100+0+0+50=150 **OJ！评测不了！害我2题爆0
还有第4题，因为少打了一个0挂了一半的点嘤嘤嘤
大佬+蒟蒻本人排行榜

姓名	得分	名次
PRJ	180	第四名
LFY	170	第六名
蒻K	150	第七名
CNH	100	第十二名

被众大佬吊打中ing。。。
放学的时候，大家还在FB。此时XC来了，因为XC听到有人报信，大家就都被D了一顿。XC走后，大家都在凉意中，有个人说了句“XC…”。结果被刚想走进来的XC听见了他的外号，于是大家又被D了一顿（巨凉）幸好我那时在上厕所（逃）
【Before 12:30】 午饭好多人啊~~~~~~·我感觉我排了半小时队。。。。。。

---

Afternoon

【Before 14:00】 又FB了一中午，竟然有小学生说Fuck Girl On the bed 很好玩。。。。。。（总结：小学生=甘地）
【Before 16:00】讲课中。。。难度：第一题<第四题<第三题<第二题
【Before 17:00】当时教室超级吵，XC又把我们D了一顿，还说了一句真理：坐越后面最弱。看着坐倒数第二排的我欣慰地笑了
【Before 18:00】去小卖部时发现由于我的RP太差，导致小卖部刚到我时机子坏了，又等了十分钟。
【Before 19:00】 回宿舍FB。突然想起今天洛谷打卡是大吉，再发现我被XCD了3次+午饭排队半小时（其实还被几个人插队了 ）+小卖店机子坏了（其实还是被大佬插队了 ）。
我知道了！由于我今天凶势太大了，所以导致连洛谷都卡BUG显示错误。。。

---

Evening

【Before 20:00】 众人FB中。。。右上方大佬提出著名格言“我拒（巨）腐”，隔壁大佬PRJ说好趴衣再腐结果还是沉迷腐中。。。后面真·神犇大佬ZYF突然坐在我后面把我吓到了
【23:20】 出艾蕾了！

---

题解

T1连续自然数和

题目描述
对一个给定的自然数M，求出所有的连续的自然数段，这些连续的自然数段中的全部数之和为M。
例子：1998+1999+2000+2001+2002 = 10000，所以从1998到2002的一个自然数段为M=10000的一个解。
注意：单个的一个数不算问题的解。

输入
一个整数M的值（10 <= M <= 2,000,000）。

输出
每行两个自然数，给出一个满足条件的连续自然数段中的第一个数和最后一个数，两数之间用一个空格隔开，所有输出行的第一个数按从小到大的升序排列，对于给定的输入数据，保证至少有一个解。

样例输入
10000

样例输出
18 142
297 328
388 412
1998 2002
----------------------------------------------------一条WA的分界线-----------------------------------------------
【难度系数】★☆☆☆☆
【核心算法】暴力枚举
【思路】①设第一项为A1,一共N项，第N项为AN= A1 +N-1,满足以下：
(A1 +AN)N/2=M，即：(2A1 +N-1)N=2M
因N<2*A1 +N-1,所以只要从枚举N到2，从而可以求出A1，当然要判断A1>0，时间复杂度为O( )
用变量
②i枚举开头的数j，从i开始不断加1，直到等于或超过m为止
③在其中用计数器sum不断累加j
④最后判断sum是否等于m，如果是则输出
⑤没有了喵
----------------------------------------------------一条RE的分界线-----------------------------------------------
代码

#include
#include
using namespace std;
int m,i,j;
int main(){
	freopen("combo.in","r",stdin);
	freopen("combo.out","w",stdout);
	cin>>m;
	for (i=1;i<=m/2;i++){//i枚举开头的数 
		int sum=0;
		for (j=i;j<m;j++){//j枚举从i开始的每一个数 
			sum+=j;//sum进行累加 
			if (sum>=m) break;
		}
		if (sum==m) cout<<i<<" "<<j<<endl;//打印输出 
	}
}

---

T2简单游戏

题目描述
Charles和sunny在玩一个简单的游戏。若给出1-n的一个排列A，则将A1、A2相加，A2、A3相加……An-1、An相加，则得到一组n-1个元素的数列B；再将B1、B2相加，B2、B3相加，Bn-2、Bn-1相加，则得到一组n-2个元素的数列……如此往复，最终会得出一个数T。而Charles和sunny玩的游戏便是，Charles给出n和T，sunny在尽可能短的时间内，找到能通过上述操作得到T且字典序最小的1~n的排列。（sunny大声说：“What an easy game！”，接着几下就给出了解），Charles觉得没意思，就想和你玩，当然，你可以用一种叫做“电子计算机”的东西帮你。

输入
本题有多组数据，对于每组数据：一行两个整数n（0

输出
对于每组测试数据输出一行n个整数，用空格分开，行尾无多余空格，表示求出来的满足要求的1~n的一个排列。

样例输入
4 16
3 9
0 0

样例输出
3 1 2 4
1 3 2
----------------------------------------------------一条MLE的分界线-----------------------------------------------
【难度系数】★★★☆☆
【核心算法】DFS+剪枝
【思路】①用变量i枚举开头的数
②j从i开始不断加1，直到等于或超过m为止
③在其中用计数器sum不断累加j
④最后判断sum是否等于m，如果是则输出
⑤没有了喵
【思路】题目要求1-N的一个排列A1,A2…An使得C(N-1,0)A1+C(N-1,1)A2+….+C(N-1,N-1)AN=T,
即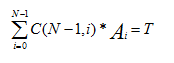： -----①式
方法很好确定，先把C（N-1，i）求出来，然后只要把每一个位上的数确定好就可以了，所以采用深度优先搜索的方法。
①方法：直接搜，用DFS(x,y)表示当前将要确定第x个位置上数，已经确定的和为y，把每种情况都搜出来，然后在递归出口的位置判断①式是否成立，不过很可惜，这种方法得不到分；
②剪枝一：加一个小小的优化，就是在确定第X个数时，保证新求出来的y不能大于T，加上这个优化后，可以得40分；
③剪枝二：由于C(N-1,i)=C(N-1,N-1-i)，具有对称性，题目又要求最小字典序列，所以在枚举时当x>n div 2 时，要保证a[x]>a[N+1-x],这样程序速度会提高，但是该题还是只能得40分；
④剪枝三：当枚举到第X个数时，剩余的N-X个数，与剩余的N-X个系数一一对应，让大数和大系数相乘，小数和小系数相乘可以得到最大值，让大数和小系数相乘，小数和大系数相乘可以得到最小值，如果剩余的值不在这个范围内，就不要搜下去，这样可以大大优化，拿样例举例来说：
N=4，T=16
⑤当枚举a[1]=1时，剩余16-11=15，剩余的未放置的数为2，3，4，剩余的系数为1，3，3，这样最大值为43+33+21=23，最小值为41+33+23=19，都超过了15，所以第一个数不能选1。
----------------------------------------------------一条WA的分界线-----------------------------------------------
代码

#include
#include
#include
#include
#include
using namespace std;

#define N 25

int f[N][N];
int q[N],t[N],x[N];
int n,m;
bool b;

void pre()
{
    memset(f,0,sizeof(f));
    f[1][1]=1;
    for (int i=2;i<N;++i)
      for (int j=1;j<=i;++j)
        f[i][j]=f[i-1][j-1]+f[i-1][j];
}

bool comp(int x,int y)
{
    return x>y;
}

bool pd(int dep,int s)
{
    int an=s;
    for (int i=dep;i<=n;++i)
      x[i-dep]=f[n][i];
    sort(x,x+n-dep+1,comp);
    int j=0;
    for (int i=n;i>=1;--i)
      if (t[i]==0)
      {
        an+=i*x[j];
        j++;
      }
    if (an<m) return true;
    an=s;
    j=0;
    for (int i=1;i<=n;++i)
      if (t[i]==0)
      {
        an+=i*x[j];
        j++;
      }
    if (an>m) return true;
    return false;
}

void dfs(int dep,int s)//dep为枚举行数/个数，s为当前累加值
{
    if (b==1) return;
    if (dep==n)//输出方案
    {
        if (s==m)
        {
            for (int i=1;i<=n;++i)
              printf("%d ",q[i]);
            printf("\n");
            b=1;
        }
        return;
    }
    if (s>m) return;
    if (pd(dep+1,s)) return;
    if (dep>n/2 && q[dep]<q[n-dep+1]) return;
    for (int i=1;i<=n;++i)//枚举数字
      if (t[i]==0)
      {
        t[i]=1;
        q[dep+1]=i;
        dfs(dep+1,s+i*f[n][dep+1]);
        t[i]=0;
      }
}

int main()
{
    pre();
    scanf("%d%d",&n,&m);
    while (not(n==0 && m==0))
    {
        b=0;
        memset(t,0,sizeof(t));
        dfs(0,0);
        scanf("%d%d",&n,&m);
    }
    return 0;
}

---

T3幸运票

题目描述
给你一个数N(1<=N<=50),每张票有2N位,同时给你这2N位上的和S,如果这张票的前N位的和等于后N位的和,那我们称这张票是吉祥的,每一位可以取0-9
你的任务是计算吉祥票的总数

输入
输入N和S,S是所以位上的和,假设S<=1000

输出
输出吉祥票的总数

样例输入
2 2

样例输出
4
----------------------------------------------------一条WA的分界线-----------------------------------------------
【难度系数】★★☆☆☆
【核心算法】递推+高精
【思路】
①题目要求组成一个2N的数，前N位的和等于后N位的和=S/2，首先考虑一个特殊情况：S=0和S=18N，答案为1。
②另前N的数字和为S/2的方法数=后N位数字和为S/2的方法数，所以答案等于ANS^2,ANS表示N的数字和为S/2的方法数。
③现在的任务就是计算ANS，很容易想到用状态f[i,j]表示i个数和为j的方法，那么ANS=f[N,S/2],怎么计算f[i,j]呢？可以从“第i上的数字是多少？”这个问题得到递推方程式：(1)j>9i时：f[i,j]=0；(2）(i=1)AND(0<=j<=9):f[1,j]=1 (3)i>1时：f[i,j]=
④时间复杂度为O(NS10),另f[i,j]具有对称性：f[i,j]=f[i,9i-j],可以把效率提高一倍。另有5个数据答案很大，要用高精度。
⑤没有了喵
----------------------------------------------------一条TLE的分界线-----------------------------------------------
代码

#include
#include
#include
using namespace std;
int n,s,f[52][1002][102],c[202];
void gzj(int x,int y,int l)//高精度加法
{
	for (int i=1;i<=100;i++)
	  {
	  	f[x][y][i]+=f[x-1][y-l][i];
	  	f[x][y][i+1]+=f[x][y][i]/10;
	  	f[x][y][i]%=10;
	  }
}
void gzc()//高精度乘法
{
	for (int i=1;i<=100;i++)
	  for (int j=1;j<=100;j++)
	    {
	    	c[i+j-1]+=f[n][s][i]*f[n][s][j];
	    	c[i+j]+=c[i+j-1]/10;
	    	c[i+j-1]%=10;
		}
}
int main()
{
	scanf("%d %d",&n,&s);
	s/=2;
	for (int i=1;i<=n;i++)//递推
	  for (int j=0;j<=s;j++)
	    if (j>i*9) continue;
	    else if (i==1&&j<=9) f[i][j][1]=1;
	    else for (int k=0;k<=min(j,9);k++) gzj(i,j,k);
	gzc();
	int p=200;
	while (!c[p]&&p) p--;
	if (!p) printf("0");
	for (int i=p;i>=1;i--)
	  printf("%d",c[i]);
	fclose(stdin);
	fclose(stdout);
	return 0;
}

---

T4抄书

题目描述
现有n本书，编号1,2,…,n。每本Pi页。全部分给m个抄写员。每人分到顺序连续的若干本，每本只分给一人。求一种方案，使每人分到的页数和的最大值为最小。输出这个值

输入
第一行两个整数N，M（0

输出
输出最佳方案的值。

样例输入
9 3
100 200 300 400 500 600 700 800 900

样例输出
1700

数据范围限制
对于10%的数据,有N<=10
对于50%的数据,有N<=500;
对于100%的数据,有N<=3000;
----------------------------------------------------一条RE的分界线-----------------------------------------------
【难度系数】★★☆☆☆
【核心算法】二分答案
【思路】①看到此题0 ②L为左边界，R为右边界，边界判断条件为L<=R。
③中间值mid=(L+R)/2，及当前设想值。构造答案为mid的方案，从后往前遵循能尽可能多抄的原则，求出所需人数X
④如果people<=M（就是所枚举的人数小于等于总人数，如果所枚举人数小于总人数，则说明X/mid值偏大）,执行R=mid-1,否则L=mid+1
⑤答案为L，该方法的时间复杂度为O(N*lg§)

----------------------------------------------------一条MLE的分界线-----------------------------------------------
代码

#include
#include
using namespace std;
int n,m,l,r,p[3005];
bool check(int x){
    int sum=0,people=0;
    for(int i=n;i>=1;i--){//从后往前枚举
    	if (p[i]>x) return false;//如果权值还比枚举的最大值大就退出
        if(i==1) people++;//第1个数特判
        if(sum+p[i]<=x) sum+=p[i];
        else people++,sum=p[i];
	}      
    return people<=m;
}
int main(){
	cin>>n>>m;
	for (int i=1;i<=n;++i) cin>>p[i],r+=p[i];
	 if (n==1){
        	cout<<p[n]<<endl;
        	return 0;
	}
	while (l<=r){//二分答案
		int mid=(l+r)/2;
		if (check(mid)) r=mid-1;
		else l=mid+1;
	}
	cout<<l<<endl;
	return 0;
}

---

相关链接

毕竟老夫也不是什么魔鬼

中山纪念中学第一份相亲文件：
关于对初中OJ“DGSSL2019卢沂锋”和“DGWGY2017陈诺涵"的相亲公告。该二位同学乃是天选之子，终成眷属。
很高兴大家来参加“DGWGY2017陈诺涵"先生和“DGSSL2019卢沂锋”小姐的结婚典礼。首先，请允许我代表二位新人向各位的到来表示忠心的感谢！（掌声）今天是公元2019年1月26日。今天世界上两个最幸福的人，他们将携手走进这个婚姻的殿堂，即将开始他们的幸福生活，在这里让我们用热烈的掌声欢迎他们的到来吧！
　　（有请新郎“DGWGY2017陈诺涵"和新娘“DGSSL2019卢沂锋”入场！接下来开始播放“结婚进行曲”）
　　（结婚进行曲中）
　　在这优美抒情浪漫的婚礼进行曲的伴凑下，在这个幸福的时刻里，在我们面前的这对新人，他们心贴着心、手牵着手，面带着微笑向我们款步走来。这预示着他们幸福生活的开始。朋友们，让我们以衷心的祝福，为他们欢呼，为他们喝彩，为了他们完美的结合，而热烈鼓掌，祝福他们拥有美好的未来！
　　（有请新郎新娘上台）
　　今天英俊潇洒的新郎和美丽漂亮的新娘终于再次牵手了。今天来参加你们婚礼的人是非常的多，可以说是高堂满坐，各位的到来给你们的婚礼带来了欢乐，同时也使得这里显得蓬壁升辉。充满了幸福的气息，下面我就介绍一下今天的主要来宾。
　　（双方的父母亲友，双方的领导，证婚人）
　　（请新郎新娘感谢来宾的到来）
滑稽