Java十大算法之动态规划算法
1.动态规划算法介绍
(1)动态规划(Dynamic Programming)算法的核心思想是:将大问题划分成小问题进行解决,从而一步步获取最优解的处理算法
(2)动态规划算法与分治算法类似,其基本思想也是将待求问题分解成若干个子问题,先求解子问题,然后从这些子问题的解得到原问题的解
(3)与分治算法不同的是,适合于动态规划求解的问题,经分解得到子问题往往不是相互独立的(即下一个子阶段的求解是建立在上一个子阶段的解的基础上,进行进一步求解)
(4)动态规划可以通过填表的方式来逐步推进,得到最优解
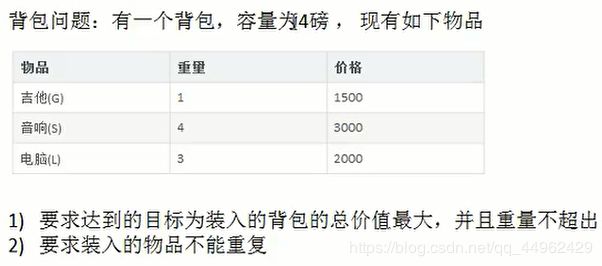
2.动态规划算法实践—背包问题
背包问题主要是指一个给定容量的背包,若干具有一定价值和重量的物品,如何选择物品放入背包使物品的价值最大?
其中分为01背包和完全背包
完全背包:每种物品都有无限件可用
01背包:每个物品最多放一个
思路分析和图解
算法的主要思想,利用动态规划来解决,每次遍历的第i个物品,根据w[i]和v[i]来确定是否需要将该物品放入背包中,即对于给定的n个物品,设v[i],w[i]分别为第i个物品的价值和重量,C为背包的容量,再令v[i][j]表示在前i个物品中能够装入容量为j的背包中的最大价值,结果如下

整理之后的公式如下:
注:如果公式看不懂,可以往上面的图片上带入,就可以理解了,这个公式一定要理解,要不代码实现更看不懂
(1)v[i][0] = v[0][j] = 0; //表示填入表的第一行和第一列都是0
(2)当w[i] > j时,v[i][j] = v[i-1][j] //当准备加入新增的商品的容量大于当前背包的容量时,就直接使用上一个单元格的装入策略
(3)当j >= w[i]时,v[i][j] = max{v[i-1][j],v[i]+v[i-1][j-w[i]]} //当准备加入的商品的新增的容量小于等于当前背包的容量
解释:
v[i-1][j]: 就是上一个单元格的装入的最大值
v[i]: 表示当前商品的价值
v[i-1][j-w[i]]: 装入i-1商品到剩余空间j-w[i]的最大值
代码实现:
package com.self.tenAlgorithm;
public class DynamicKnapsackProblem {
public static void main(String[] args) {
int[] w = {1,4,3}; //物品的重量
int[] val = {1500,3000,2000}; //物品的价值 这里的val[i] ,就是前面的v[i}
int m = 4; //背包的容量
int n = val.length; //物品的个数
//v[i][j] 表示在前i个物品中能够装入容量为j的背包中的最大值
//因为第一行的第一列都是0 所以我们的m,n都加1
int[][] v = new int[n + 1][m + 1];
//为了记录放入商品的情况,我们定一个二维数组
int[][] path = new int[n+1][m+1];
//第一行和第一列都是0,初始化第一行第一列
for (int i = 0; i < v.length; i++) {
v[i][0] = 0; //将第一列设置为0
}
for (int i = 0; i < v[0].length; i++) {
v[0][i] = 0; //将第一行设置为0
}
//动态规划处理
for (int i = 1; i < v.length; i++) { //不处理第一行
for (int j = 1; j < v[0].length; j++) { //不处理第一列
if(w[i-1] > j){ //因为i是从一开始的
v[i][j] = v[i-1][j];
}else{
//因为i是从1开始的 所以之前推到的公式也需要调整
//v[i][j] = Math.max(v[i - 1][j],val[i - 1] + v[i - 1][j - w[i - 1]]);
// 因为我们最后输出的结果就是想看到都有哪几个商品放入背包,所以对原始公式做调整
if(v[i - 1][j] < val[i - 1] + v[i - 1][j - w[i - 1]]){
v[i][j] = val[i - 1] + v[i - 1][j - w[i - 1]];
path[i][j] = 1;
}else{
v[i][j] = v[i-1][j];
}
}
}
}
for (int i = 0; i < v.length; i++) {
for (int j = 0; j < v[0].length; j++) {
System.out.print(v[i][j]+"\t");
}
System.out.println();
}
int i = path.length - 1; //行的最大下标
int j = path[0].length - 1; //列的最大下标
while (i > 0 && j > 0){
if(path[i][j] == 1){
System.out.printf("第%d个商品放入背包\n",i);
j -= w[i - 1];
}
i--;
}
}
}