机器学习之Knn算法
一、机器学习Machine Learning(ML)
1.1 概念
| 人工智能Artificial Intelligence(AI)、机器学习Machine Learning(ML)和深度学习Deep Learning(DL) |
|---|
 |
(1)Artificial Intelligence:Artificial就意味着由人开发或本来不存在的东西构成。Intelligence意味着它有自主理解和思考的能力。一个系统能获取外部数据并从这些数据中学习,并能利用学习到的知识来灵活适应特定的目标和任务的能力。技术层主要分为三个领域:机器学习、语音识别和自然语言处理、以及计算机视觉
(2)Machine Learning:机器学习可以认为是一种数据驱动的决策方法,是人工智能的一种应用,为AI提供了一种自学习的能力。一般在机器学习任务中,我们都会定义具体的目标Goal和评估标准Metrics。机器学习可以不断地学习数据和计算评估标准并迭代来达到Goal。
(3)**Deep Learning:**深度学习是一种机器学习方法,隶属于机器学习中增强学习的范畴。
1.2 机器学习ML发展
推理期(20世纪50-70年代初)
- 认为只要给机器赋予逻辑推理能力,机器就具有智能
- A.Newell和H.Simon的“逻辑理论家”“通用问题求解”程序,获得1975年图灵奖
知识期(20世纪70年代中期)
- 认为要使机器具有智能,就必须设法使机器拥有知识
- E.A.Feigenbaum作为“知识工程”之父获得1994年图灵奖
学科形成(20世纪80年代)
- 机器学习成为一个独立学科领域并快速发展,各种机器学习技术百花齐放
繁荣期(20世纪80年代至今)
-
20世纪90年代后,统计学方法占主导,代表为SVM
-
数据即算法?——开启大数据时代
-
2006年至今,基于大数据分析的需求,神经网络又被重现,成为深度学习理论的基础
-
算法为王?——算法再次被人们重视
1.2 机器学习ML的分类
机器学习可以在与数据交互层面、任务处理层面、学习模式层面等不同角度有很多分类,较常见的是与数据交互层面的分类。
(1)监督学习:特点就是喂给机器的数据都是有标记与答案的,机器根据这些标记或者说是特征feature进行分类处理,比如分类算法KNN
(2)非监督学习:无标记情况下,通过对特征提取、数据压缩或者PCA降维等方式进行的分类聚合,后期随着数据量增大逐渐呈现一定的分类特征,最终转为监督学习,比如用户画像
(3)增强学习:根据环境的反馈自我调整,自我学习,
深度学习隶属于此范畴,比如阿尔法狗Zero
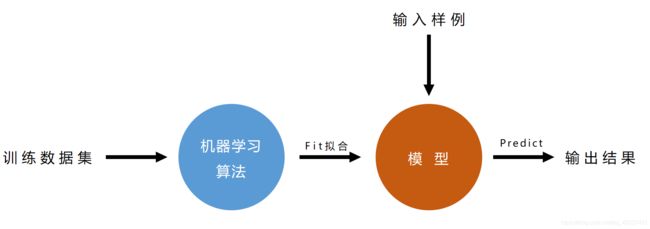
1.3 机器学习的整体流程
| 机器学习的宏观流程 |
|---|
 |
二、数据集dataSet
2.1 概念
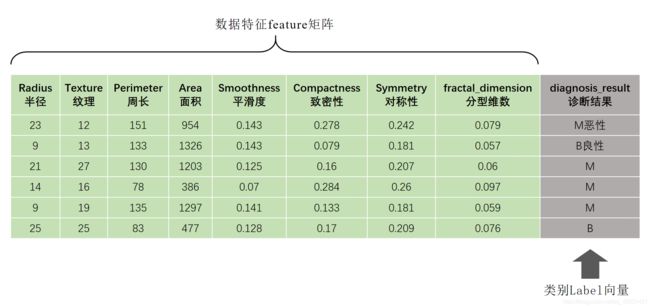
每个样本sample都是一个数据集dataset。样本的特征feature构成了特征矩阵,样本的类别(或者说是标签)Label构成了一维向量。
在机器学习中,操作最多的就是矩阵和向量,矩阵就是一个二维或者多维的数组,向量一般为一维的数组,用于表示每个样本的类别
f e a t u r e 矩 阵 = [ 23 12 151 954 0.143 0.278 0.242 0.079 9 13 133 1326 0.143 0.079 0.181 0.057 21 27 130 1203 0.125 0.16 0.207 0.06 ] l a b e l 标 签 = [ 1 , 0 , 1 ] feature矩阵 = \left[ \begin{matrix} 23 & 12 & 151 & 954 & 0.143 & 0.278 & 0.242 & 0.079 \\ 9 & 13 & 133 & 1326 & 0.143 & 0.079 & 0.181 & 0.057 \\ 21 & 27 & 130 & 1203 & 0.125 & 0.16 & 0.207 & 0.06 \end{matrix} \right] label标签 = [1, 0, 1] feature矩阵=⎣⎡23921121327151133130954132612030.1430.1430.1250.2780.0790.160.2420.1810.2070.0790.0570.06⎦⎤label标签=[1,0,1]
在数据处理时,往往需要将矩阵和向量拆开。
2.2 数据归一化处理
在肿瘤数据集dataSet中,各特征指标之间的值相差很大,主要原因就是量纲(单位)不同导致的,而各个数据的量纲维度又没有换算关系。
数据集里的大数在我们进行算法处理的时候,会处于主导地位,而小数则往往会被忽略,从而导致预测结果不准确,所以我们要统一化量纲。
归一化原则就是将所有数据等比压缩到一个 [0,1] 的区间中
两种常用的归一化方法:最值归一化 和 均值方差归一化
1、
最值归一化,将所有数据映射到同一个尺度中
x s c a l e = x − x m i n x m a x − x m i n x_{scale} = \frac{x-x_{min}}{x_{max}-x_{min}} xscale=xmax−xminx−xmin
这种方法适用于分布有明显边界的情况2、
均值方差归一化,将所有数据归一到一个均值为0,方差为1的正态分布中
x s c a l e = x − x m e a n S x_{scale} = \frac{x-x_{mean}}{S} xscale=Sx−xmean
2.3 数据分类的二八原则
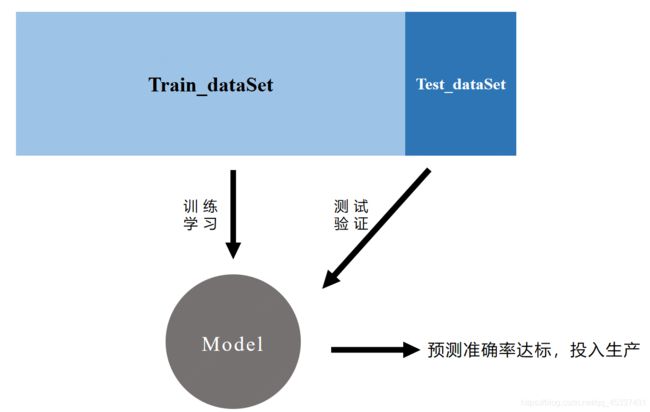
机器学习的整体流程中,会在训练阶段和测试阶段喂给机器数据,所以我们需要将整体的数据集分为两个部分:训练数据集train_dataset 和 测试数据集test_dataset
一般的训练数据占总体数据的80%,测试数据占总体数据的20%
| 数据的二八分类原则 |
|---|
 |
三、KNN算法
3.1 概念
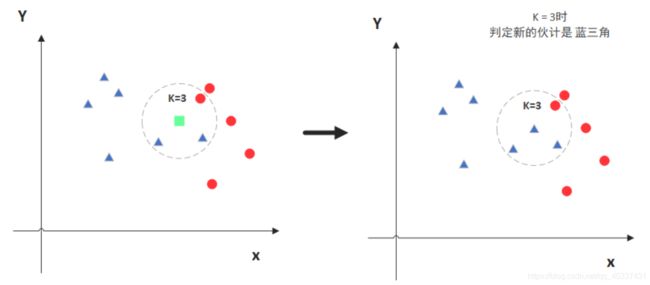
KNN的全称是K Nearest Neighbors(最值临近),意思是K个最近的邻居,是最简单且最常用的算法,属于监督学习中的分类算法范畴。
 |
|---|
原理:选举投票原则,当传入一个新的参数方块的时候,找到离方块最近的k(k=3)个点,然后投票,如果这三个点中lable=三角的个数最多,则说明参数方块属于三角类的标签 |
3.2 调参——超参数的选取
机器学习中的参数主要有两种:超参数和模型参数。
超参数:算法在运行之前决定的参数,比如KNN算法中的k值大小。在算法工程中,更多时候都是在调校超参数。
模型参数:算法运行过程中机器学习的参数。
在KNN算法中,根据我们的需求会对1个或者多个超参数进行校准,随着超参数越多,效率也会越慢。
3.2.1 超参数——k的最佳值
KNN算法中,对于k的选择依据一共有三种:
(1)领域知识
(2)经验数值
(3)实验搜索,即不断对机器进行训练和测试,以谋求最佳的k值
3.2.2 超参数——距离权重
选举投票过程中,票数最多的类并不一定距离新参更近,所以我们需要计算k个点到新参之间的距离,取倒数求得权重,距离越近权重越大。
距离的计算公式:
明可夫斯基距离
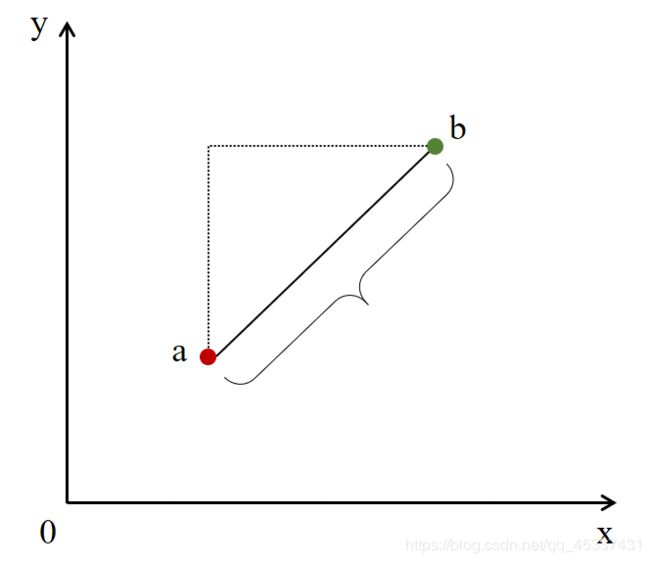
d i s t a n c e = ( ∑ i = 1 n ∣ X i ( a ) − X i ( b ) ∣ p ) 1 p 说 明 : a 和 b 表 示 两 个 点 , n 表 示 数 据 维 度 ( 即 特 征 f e a t u r e ) distance = (\sum_{i=1}^n|X^{(a)}_{i}-X^{(b)}_{i}|^{p})^{\frac{1}{p}} \\说明:a和b表示两个点,n表示数据维度(即特征feature) distance=(i=1∑n∣Xi(a)−Xi(b)∣p)p1说明:a和b表示两个点,n表示数据维度(即特征feature)
(1)当p=1的时候是曼哈顿距离,计算的是各个数据维度的差值,再求和(2)当p=2的时候是欧拉距离,即各个维度坐标值差的平方和再开根号
曼哈顿距离 欧拉距离
3.2.3 超参数——p的最佳值
如果引入了明可夫斯基距离,就不可避免的要考虑随之而来的另一个超参数p,同样p的取值依据与k一样,根据知识、经验、试验验证方式进行选择,但此时,KNN算法的计算量非常巨大。
3.2.4 超参数——距离计算方法的类型选择
除了明可夫斯基距离、曼哈顿距离以及欧拉距离以外,还有四种距离计算的方法
(1)向量空间余弦相似度Cosine Similarity
(2)调整余弦相似度 Adjusted Cosine Similarity
(3)皮尔森相关系数 Pearson Correlation Coefficient
(4)Jaccard相似系数 Jaccard Coefficient
四、KNN算法的优缺点
4.1 优点
-
可以处理分类问题,同时天然可以处理多分类问题
-
KNN还可以处理回归问题,也就是预测
-
简单,易于理解,易于实现
-
不易受小错误概率的影响
-
在手写识别领域应用很广,采集多人的手写字数据,根据每个像素块对应的灰度值特征进行分类,预测准确率高
4.2 缺点
- 效率低,m个样本,n个维度,时间复杂度达到了O(m,n)
- 高度的数据相关,会因为某一个异常数据导致结果不准确,所以除了进行归一处理,还要进行异常数据检测处理
- 维数灾难,经计算,随着维数的增加,看似相近的两个点之间的距离越来越大,就会越来越“不像,最终影响准确率。所以在对高维数据进行处理的时候,需要使用PCA算法降维
案例
我们这里选择从scikit-learn中获取的关于肿瘤的诊断数据进行案例演示,代码如下,感兴趣的伙伴可以试着玩玩:
"""
运行的main函数
"""
import dataset as ds
import model_selection as ms
import model_picture as mp
import model_knn as mk
# 读取csv文件获取数据集
tumourData = ds.tumourDataSet("E:\\tumor.csv")
# 获取feature_names特征名称
feature_names = tumourData.feature_names
# 获取特征数据矩阵
X = tumourData.data
# 获取target标签名称
target_names = tumourData.target_names
# 获取target标签向量
y = tumourData.target
# 输出显示
print('feature_names\n', feature_names, '\n\n', 'data\n', X,
'\n\n', 'target_names\n', target_names, '\n\n', 'target\n', y)
# 分为80%训练集和20%测试集
X_train, X_test, y_train, y_test = ms.train_test_split(X, y, seed=100)
print(X_train.shape, "\n", X_train, "\n\n")
print(y_train.shape, "\n", y_train)
# 二维散点图
# 1-纹理;3-面积;4-平滑度;5-致密性;6-对称性;7-分型维度
mp.picture2D(X_train[:, 5], X_train[:, 6], y_train, feature_names[5], feature_names[6])
# 测试预测准确率
mk.normal_knn(X_train, y_train, X_test, y_test)
# # 寻找最佳k值
mk.bestOfk_knn(X_train, y_train, X_test, y_test, 11)
# 寻找最佳距离
mk.best_k_p_knn(X_train, y_train, X_test, y_test, 11, 6)
# 网格交叉搜索
mk.best_grid_search(X_train, y_train, X_test, y_test, 11, 6)
"""
读取文件,并转为标准的数据集tumourDataSet函数
"""
import pandas as pd
import numpy as np
from sklearn.preprocessing import MinMaxScaler
class Tumour:
def __init__(self, feature_names, data, target_names, target):
self.feature_names = feature_names
self.data = data
self.target_names = target_names
self.target = target
# 数据集处理函数
def tumourDataSet(url):
# 读取文件为dataFrame:"E:\\周会分享\\机器学习之knn算法\\tumor.csv"
dataFrame = pd.read_csv(url)
# 转为数据矩阵
csv_matrix = dataFrame.values
# 数据的拆分为如下形式: 特征名称,特征矩阵,标签名称,标签向量
# feature_names 特征名称(表头)
feature_names = dataFrame.columns.values[:-1]
# data 特征数据矩阵
data = csv_matrix[:, :-1]
# 数据归一化处理
minmaxScaler = MinMaxScaler()
minmaxScaler.fit(data)
data = minmaxScaler.transform(data)
data = np.around(data, decimals=2)
# target_names 标签名称
target_names = np.array(['Benign:0', 'Malignant:1'])
# target 标签数据向量,0表示Benign良性,1表示Malignant恶性
target = csv_matrix[:, -1]
target[target == 'M'] = 1
target[target == 'B'] = 0
# 这里必须规定转化的基本数据类型,否则无法预测
target = target.astype(int)
# 返回Tumour对象
return Tumour(feature_names, data, target_names, target)
"""
分为80%训练集和20%测试集
"""
import numpy as np
# 定义切分函数,传入特征矩阵和类别向量,test_ratio表示测试数据占比
def train_test_split(X, y, test_ratio = 0.2, seed = None):
assert X.shape[0] == y.shape[0], \
"the size of X must be equal to the size of y"
assert 0.0 <= test_ratio <= 1.0, \
"test_ratio must be valid"
if seed:
np.random.seed(seed)
# 打乱样本索引,使用索引可以保证向量和特征矩阵一一对应
shuffle_index = np.random.permutation(len(X))
# 获取测试和训练数据集的索引
test_size = int(len(X) * test_ratio)
test_index = shuffle_index[:test_size]
train_index = shuffle_index[test_size:]
# 训练样本特征矩阵和测试样本特征矩阵
X_train = X[train_index]
X_test = X[test_index]
# 训练和测试的标签向量
y_train = y[train_index]
y_test = y[test_index]
return X_train, X_test, y_train, y_test
"""
绘制散点图
"""
import matplotlib as mpl
import matplotlib.pyplot as plt
import mpl_toolkits.mplot3d.axes3d
import numpy as np
def picture3D(X_train_x, X_train_y, X_train_z, y_train):
# 定义坐标轴
ax1 = plt.axes(projection='3d')
ax1.scatter3D(X_train_x[y_train == 0], X_train_y[y_train==0], X_train_z[y_train==0], color='green', marker='o')
ax1.scatter3D(X_train_x[y_train == 1], X_train_y[y_train==1], X_train_z[y_train==1], color='red', marker='o')
plt.show()
def picture2D(X_train_x, X_train_y, y_train, x_label, y_label):
plt.scatter(X_train_x[y_train == 0], X_train_y[y_train == 0], color='green', marker='x', label="Benign")
plt.scatter(X_train_x[y_train == 1], X_train_y[y_train == 1], color='red', marker='o', label="Malignant")
plt.xlabel(x_label)
plt.ylabel(y_label)
plt.legend()
plt.show()
"""
各种knn超参数的调节
"""
from sklearn.neighbors import KNeighborsClassifier as knnClassifier
import time
from sklearn.model_selection import GridSearchCV
# 普通的knn算法
def normal_knn(X_train, y_train, X_test, y_test):
# 使用KNN算法,n_neighbors为k值,X_train训练数据集存入,进行拟合;X_test作为测试
kNN_classifier = knnClassifier(n_neighbors=6)
# 传入训练集
kNN_classifier.fit(X_train, y_train)
# 传入测试集,打印预测准确率
score = kNN_classifier.score(X_test, y_test)
print(score)
# 寻找最佳k值
def bestOfk_knn(X_train, y_train, X_test, y_test, max_range):
best_score = 0.0
best_k = -1
for k in range(1, max_range):
kNN_classifier = knnClassifier(n_neighbors=k)
kNN_classifier.fit(X_train, y_train)
score = kNN_classifier.score(X_test, y_test)
if score > best_score:
best_k = k
best_score = score
print("best_k = ", best_k)
print("best_score", best_score)
# 寻找明可夫斯基公式最佳p值
def best_k_p_knn(X_train, y_train, X_test, y_test, max_k_range, max_p_range):
start = time.time()
best_score = 0.0
best_k = -1
best_p = -1
for k in range(1, max_k_range):
for p in range(1, max_p_range):
kNN_classifier = knnClassifier(n_neighbors=k, weights="distance", p = p)
kNN_classifier.fit(X_train, y_train)
score = kNN_classifier.score(X_test, y_test)
if score > best_score:
best_k = k
best_score = score
best_p = p
end = time.time()
print("best_k = ", best_k)
print("best_p = ", best_p)
print("best_score", best_score)
print("best_k_p_knn_code run-time:", end-start, " seconds")
# 网格搜索,交叉处理:在只考虑k和考虑k&p两种情况下进行择优
def best_grid_search(X_train, y_train, X_test, y_test, max_k_range, max_p_range):
start = time.time()
param_grid = [
{
'weights':['uniform'],
'n_neighbors':[i for i in range(1, max_k_range)]
},{
'weights': ['distance'],
'n_neighbors': [i for i in range(1, max_k_range)],
'p':[i for i in range(1, max_p_range)]
}
]
knn_clf = knnClassifier()
# 将网格参数和KNeighborsClassifier传入网格,告诉网格进行knn算法处理, n_jobs表示处理器,verbose表示打印详细信息
grid_search = GridSearchCV(knn_clf, param_grid, n_jobs=-1, verbose=2)
# 训练数据集存入
grid_search.fit(X_train, y_train)
# 选择出最佳模型
knn_clf = grid_search.best_estimator_
score = knn_clf.score(X_test, y_test)
end = time.time()
print("Best-model:", knn_clf, "\n", "Best-score:", score, "\n", "best_grid_search-runTime:", end-start)
参考文章:
- 读芯术《5分钟看完70年机器学习史,我膨胀了》
- 大数据mp媒体号《机器学习重大挑战:坏数据和坏算法正在毁掉你的项目》
- zzzzMing -大数据技术
- scikit-learn学习网站