机器学习1:关联分析及频繁模式挖掘Association rule mining(基于R language)
关联分析是一种无监督的机器学习方法,常用于知识发现而非预测。本文从以下几个方面进行叙述:
- 频繁项 Frequent Patterns
- 关联挖掘方法 Association Mining Methods
- apriori
- ECLAT
- 关联规则 Association Rules
- 评价方法 Correlations-Pattern Evaluation Methods
关联分析
- 举例
- 应用
- 原理
- 一、频繁项及几个必知必会的定义
- 二、关联挖掘方法
- 算法1:Apriori算法
- 算法2:ECLAT算法 Equivalence Class Transformation
- 三、关联规则
- 1.名词定义
- 2.关联规则生成步骤
- 四、关联项评价方法:规则是否interesting?
- 相关关系评价指标1:卡方 X 2 X^2 X2
- 相关关系评价指标2:提升值Lift
- 五、代码
- Apriori算法找频繁项集
- 算法1:Apriori算法找频繁项集&关联规则
- 算法2:ECLAT算法找频繁项集
- interesting检验
- 可视化操作
- 利用关联规则做分类
- 说明&致谢
- 参考资料
举例
关联分析的动机:寻找数据的固有规律
1.消费者通常一起购买什么产品?— 啤酒和尿布经典例子?!
2.顾客购买电脑后,以后会购买什么? 哪种DNA对这种新药敏感?
3.我们可以自动对Web文档进行分类吗?
应用
1.市场篮子分析 Basket data analysis
2.交叉营销 Cross-marketing
3.目录设计 Catalog design
4.促销活动分析 Sale campaign analysis
5.网路日志分析 Web log analysis
6.DNA序列分析 DNA sequence analysis
…
原理
一、频繁项及几个必知必会的定义
(1)项集 Itemset:一个或多个项组成的集合;
(2)k-项集 k-itemset:包含k个事物的集合, X = { x 1 , x 2 , ⋯ , x k } X=\{x_1,x_2,\cdots,x_k\} X={x1,x2,⋯,xk};
(3)(绝对)支持/支持计数 (absolute) support:一个项集出现在几个观测当中,它的支持度计数就是几;
(4)(相对)支持/支持度 (relative) support:支持度计数除于总的观测数;
(5)频繁项集:当该项集的支持度/支持度计数大于一个阈值minsup(一般来说,minsup<0.1),该项集就称为频繁项。
例
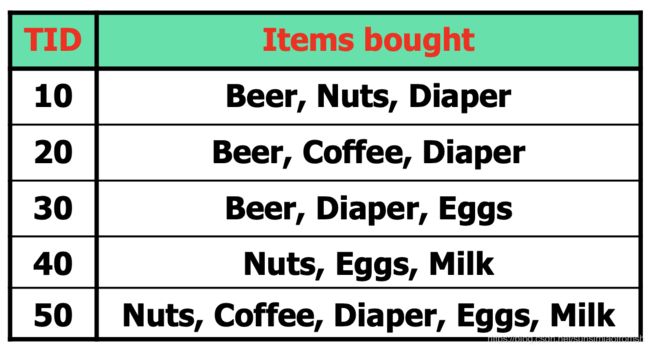
1.计算{Beer},{Diaper},{Coffee}和{Beer,Diaper}的支持度计数/支持度。
TID为观测号,一共有5个观测;Items bought为每个观测中包含的物品;我们用{物品1}/{物品1,物品2}/{物品1,物品2,物品3}/…这样的集合来表示包含1/2/3…个物品的项集,其中物品i就称为一个项。
{Beer},Beer在10、20和30观测中出现,故支持度计数为3,支持度为 3 5 ∗ 100 % = 60 % \frac{3}{5}*100\%=60\% 53∗100%=60%
{Diaper},Diaper在10、20、30和50观测中出现,故支持度计数为4,支持度为 4 5 ∗ 100 % = 80 % \frac{4}{5}*100\%=80\% 54∗100%=80%
{Coffee},Coffee在20和50观测中出现,故支持度计数为2,支持度为 2 5 ∗ 100 % = 40 % \frac{2}{5}*100\%=40\% 52∗100%=40%
{Beer,Diaper},Beer,Diaper同时出现在10、20和30观测中出现,故支持度计数为3,支持度为 3 5 ∗ 100 % = 60 % \frac{3}{5}*100\%=60\% 53∗100%=60%
2.当minsup=50%,{Beer},{Diaper},{Coffee}和{Beer,Diaper}哪些项集是频繁的?哪些不频繁?
题干所述4个项集,支持度大于50%的有{Beer},{Diaper}和{Beer,Diaper},故这3个项集是频繁的。
二、关联挖掘方法
算法1:Apriori算法
Apriori12采用“自下而上”的方法(称为“向下闭关属性”),其中频繁的子集一次扩展一项(称为“候选生成”),然后针对数据测试候选组是否频繁,即通过1项频繁集可以得到所有可能的2项频繁集候选者,然后通过测试来确定这些候选者中的真正频繁的二项集。
原理:如果某个项集是频繁项集,那么它所有的子集也是频繁的。那么k项集为频繁项集,那所有的k+1项集必须包含k项集。因此,若k项集为非频繁项集,那所有的k+1项集必然是非频繁项集。
Apriori采用的是横向优先的搜索方法。
具体步骤如下:
1.首先,扫描数据库以获得频繁的1项集;
2.在k项频繁集上增加一项,得到所有可能频繁的k+1项候选集;
3.根据minsup选取k+1项频繁集;
4.当无法生成频繁集/候选集时停止。
接下来介绍一个Apriori算法的例子: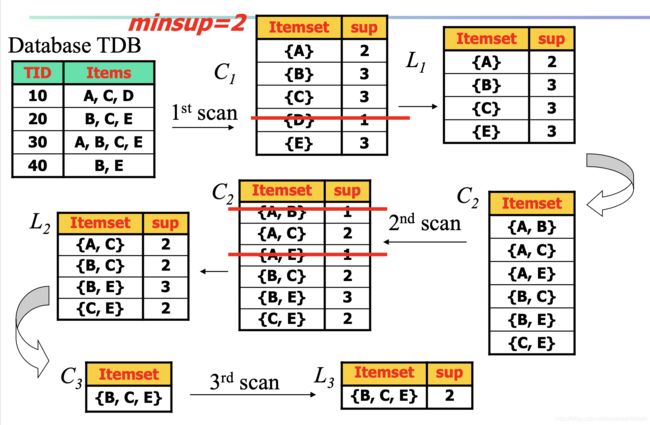
例
设定支持度计数阈值minsup=2:
1.列出所有1项集及其支持度计数,由上图可知所有一项集中仅有{D}的支持度计数=1,不频繁,故删去;
2.列举所有频繁1项集{A}、{B}、{C}和{E}可以构成的2项集,即{A,B}、{A,C}、{A,E}、{B,C}、{B,E}和{C,E},由上图可知{A,B}和{A,E}的支持度计数分别=1和1,小于minsup,故删去;
3.继续通过频繁2项集{A,C}、{B,C}、{B,E}和{C,E}产生所有3项集,即{A,B,C}、{A,C,E}和{B,C,E},它们的支持度计数分别=0,0和2,仅有{B,C,E};
4.无法再生成4项集,故停止算法。

Apriori算法的优缺点如下:
| 优点 | 缺点 |
|---|---|
| 适用于大量交易数据 | 不适用于小型数据库 |
| 规则易懂 | 很难脱离常识 |
| 对数据挖掘十分有用,可以探索性研究一个数据库 | 容易从随机项集得出虚假结论 |
算法2:ECLAT算法 Equivalence Class Transformation
与Apriori算法不同,采用的是深度优先的搜索方法。这是一种自然优雅的算法,适用于顺序执行和并行执行,并具有局部性增强特性。
ECLAT算法的步骤不是一个个找频繁项集,而是找每个项属于哪些观测,再找项 X,Y 观测的交集,就找到了{X,Y} 所属的观测。ECLAT算法的步骤可以通过以下两张图来解释:

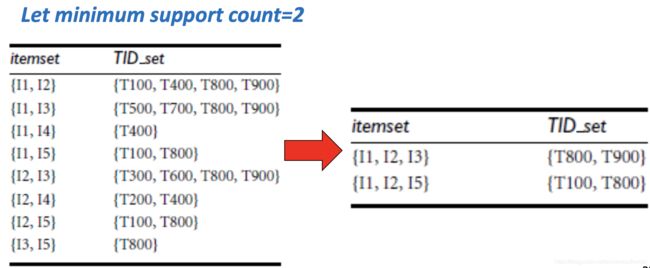
三、关联规则
1.名词定义
(1)规则 rule: X ⟹ Y X\Longrightarrow Y X⟹Y,意味着“X会影响Y”;
- X 左项集lhs;
- Y 右项集rhs。
(2)置信度 confidence:含有X的交易观测也含有Y的条件概率;
c o n f i d e n c e ( X ⟹ Y ) = P ( Y ∣ X ) = P ( X , Y ) P ( X ) = s u p p o r t ( X ⟹ Y ) s u p p o r t ( X ) confidence(X\Longrightarrow Y)=P(Y|X)=\frac{P(X,Y)}{P(X)}=\frac{support(X\Longrightarrow Y)}{support(X)} confidence(X⟹Y)=P(Y∣X)=P(X)P(X,Y)=support(X)support(X⟹Y)
其中, s u p p o r t ( X ⟹ Y ) support(X\Longrightarrow Y) support(X⟹Y)为同时包含 X,Y 的观测数,即包含 X,Y 并集的观测数; s u p p o r t ( X ) support(X) support(X)为包含X的观测数。
- 置信度 P ( Y ∣ X ) P(Y|X) P(Y∣X)大,说明X对Y有促进作用;
- 置信度 P ( Y ∣ X ) P(Y|X) P(Y∣X)小,说明X对Y有抑制作用。
(3)强关联规则 strong association rule:满足 s u p p o r t ( X ⟹ Y ) ≥ m i n s u p , c o n f i d e n c e ( X ⟹ Y ) ≥ m i n c o n f support(X\Longrightarrow Y)\geq minsup,\ confidence(X\Longrightarrow Y)\geq minconf support(X⟹Y)≥minsup, confidence(X⟹Y)≥minconf的规则成为强关联规则(通常minsup<0.1,0.6<minconf<0.8)。
2.关联规则生成步骤
(1)对每个频繁项集l,生成其非空子集u;
(2)对每个非空子集u,输出一个规则 u ⟹ ( l − u ) u\Longrightarrow (l-u) u⟹(l−u);
(3)选择强关联规则。

例
设minsup=50%,minconf=50%,考虑频繁项集{Beer,Diaper}产生的规则:
B e e r ⟹ D i a p e r Beer \Longrightarrow Diaper Beer⟹Diaper: s u p p o r t ( B e e r , D i a p e r ) = 60 % support(Beer,Diaper)=60\% support(Beer,Diaper)=60%, c o n f i d e n c e ( B e e r ⟹ D i a p e r ) = 60 % 60 % = 100 % confidence(Beer \Longrightarrow Diaper)=\frac{60\%}{60\%}=100\% confidence(Beer⟹Diaper)=60%60%=100%
D i a p e r ⟹ B e e r Diaper \Longrightarrow Beer Diaper⟹Beer: s u p p o r t ( D i a p e r , B e e r ) = 60 % support(Diaper,Beer)=60\% support(Diaper,Beer)=60%, c o n f i d e n c e ( D i a p e r ⟹ B e e r ) = 60 % 80 % = 75 % confidence(Diaper \Longrightarrow Beer)=\frac{60\%}{80\%}=75\% confidence(Diaper⟹Beer)=80%60%=75%
因此 B e e r ⟹ D i a p e r Beer \Longrightarrow Diaper Beer⟹Diaper和 D i a p e r ⟹ B e e r Diaper \Longrightarrow Beer Diaper⟹Beer都是强关联规则。
四、关联项评价方法:规则是否interesting?
强关联规则可能是具有误导性的! 因此我们要通过显著性检验来判断一个规则是否是interesting。

例
假如设定minconf=0.6,那么 p l a y b a s k e t b a l l ⟹ e a t c e r e a l \ play basketball \Longrightarrow eat cereal playbasketball⟹eatcereal毋庸置疑是一个强关联规则,但事实上调查显示,所有学生(无论打不打篮球)“吃谷物”的比例为75%,这个比例比该关联规则的置信度66.7%要高,暗示了“打篮球”的人可能更加会选择“不吃谷物”。
相比而言,虽然支持度和置信度都很低,但 p l a y b a s k e t b a l l ⟹ n o t e a t c e r e a l \ play basketball \Longrightarrow not eat cereal playbasketball⟹noteatcereal这个规则描述两者关系更为准确。
鉴于支持度和置信度用来评价相关关系的效果不大好,可以选择以下两种指标来作为评价指标:
相关关系评价指标1:卡方 X 2 X^2 X2
列联表检验。
相关关系评价指标2:提升值Lift
提升值是衡量提升程度的指标,即,与事件B本身发生概率相比——用P(B)来表示,事件A的存在提升事件B发生概率——P(B|A)——的程度。lift的公式定义如下:
l i f t = P ( A B ) P ( A ) P ( B ) = P ( B ∣ A ) P ( B ) = c o n f i d e n c e ( A ⟹ B ) s u p p o r t ( B ) lift=\frac{P(AB)}{P(A)P(B)}=\frac{P(B|A)}{P(B)}=\frac{confidence(A \Longrightarrow B)}{support(B)} lift=P(A)P(B)P(AB)=P(B)P(B∣A)=support(B)confidence(A⟹B)
- l i f t < 1 lift<1 lift<1,A和B负相关;
- l i f t = 1 lift=1 lift=1,A和B独立,即,A和B没有关系;
- l i f t > 1 lift>1 lift>1,A和B正相关。
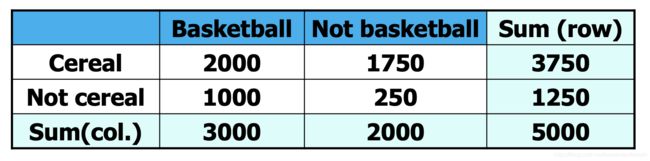
例
事件B=“打篮球”,事件C=“吃谷物”
l i f t ( B ⟹ C ) = 2000 / 5000 3000 / 5000 ∗ 3750 / 5000 = 0.89 < 1 lift(B \Longrightarrow C)=\frac{2000/5000}{3000/5000*3750/5000}=0.89<1 lift(B⟹C)=3000/5000∗3750/50002000/5000=0.89<1
l i f t ( B ⟹ C ˉ ) = 1000 / 5000 3000 / 5000 ∗ 1250 / 5000 = 1.33 > 1 lift(B \Longrightarrow \bar{C})=\frac{1000/5000}{3000/5000*1250/5000}=1.33>1 lift(B⟹Cˉ)=3000/5000∗1250/50001000/5000=1.33>1
因此,“打篮球”对“吃谷物”起抑制作用,“打篮球”对“不吃谷物”起促进作用。
五、代码
例 采用Groceries(transactions类型)作为例子
data("Groceries")
Groceries
inspect(Groceries[1:10])
用inspect函数可以看到10个购物篮所含商品(项)分别如下:
## items
## [1] {citrus fruit,
## semi-finished bread,
## margarine,
## ready soups}
## [2] {tropical fruit,
## yogurt,
## coffee}
## [3] {whole milk}
## [4] {pip fruit,
## yogurt,
## cream cheese ,
## meat spreads}
## [5] {other vegetables,
## whole milk,
## condensed milk,
## long life bakery product}
## [6] {whole milk,
## butter,
## yogurt,
## rice,
## abrasive cleaner}
## [7] {rolls/buns}
## [8] {other vegetables,
## UHT-milk,
## rolls/buns,
## bottled beer,
## liquor (appetizer)}
## [9] {pot plants}
## [10] {whole milk,
## cereals}
summary(Groceries)
通过summary可以得到的信息为:
1.总共有9835条交易记录(交易观测),其中涉及169个商品(项)。density=0.026表示在稀疏矩阵中1的百分比;
2.在这些交易观测中,最频繁出现的商品分别为whole milk(2513次),other vegetables(1903次),rolls/buns(1809次),soda(1715次),yogurt(1372次),剩余商品出现次数总和为34055次。可以计算出最大支持度(whole milk的支持度);
3.每笔交易包含的商品数目,即k项集( k = 1 , 2 , ⋯ k=1,2,\cdots k=1,2,⋯)的个数。如:2159条交易仅包含了1个商品(1项集2159个),1643条交易购买了2件商品(2项集1643个),1条交易购买了32件商品(32项集1个);
4.5⃣️个分位数和均值的统计信息。含义是:下四分位数为2,意味着25%的交易包含不超过2个商品;中位数为3,意味着50%的交易购买的商品不超过3件;均值为4.4,表示所有的交易平均购买4.4件商品。
5.如果数据集包含除了Transaction Id 和 Item之外的其他的列(如,发生交易的时间,用户ID等等),会显示在这里。这个例子,其实没有新的列,labels就是item的名字。3
## transactions as itemMatrix in sparse format with
## 9835 rows (elements/itemsets/transactions) and
## 169 columns (items) and a density of 0.02609146
##
## most frequent items:
## whole milk other vegetables rolls/buns soda
## 2513 1903 1809 1715
## yogurt (Other)
## 1372 34055
##
## element (itemset/transaction) length distribution:
## sizes
## 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15
## 2159 1643 1299 1005 855 645 545 438 350 246 182 117 78 77 55
## 16 17 18 19 20 21 22 23 24 26 27 28 29 32
## 46 29 14 14 9 11 4 6 1 1 1 1 3 1
##
## Min. 1st Qu. Median Mean 3rd Qu. Max.
## 1.000 2.000 3.000 4.409 6.000 32.000
##
## includes extended item information - examples:
## labels level2 level1
## 1 frankfurter sausage meat and sausage
## 2 sausage sausage meat and sausage
## 3 liver loaf sausage meat and sausage
arules包里有关联分析所需函数,其中包含了apriori函数(apriori算法)和eclat函数(eclat算法)。
library(arules) # 安装arules包
对Groceries数据进行探索性研究:
class(Groceries) # 查看数据类型
## [1] "transactions"
## attr(,"package")
## [1] "arules"
head(colnames(Groceries)) # 展示前6个商品名称
## [1] "frankfurter" "sausage" "liver loaf" "ham"
## [5] "meat" "finished products"
size(Groceries) # 展示每笔交易包含商品个数
min(size(Groceries)) # 最小个数
max(size(Groceries)) # 最大个数
itemFrequency(Groceries) # 每个商品的支持度计数
sum(itemFrequency(Groceries)) # 平均每笔交易包含商品个数
> 4.409456
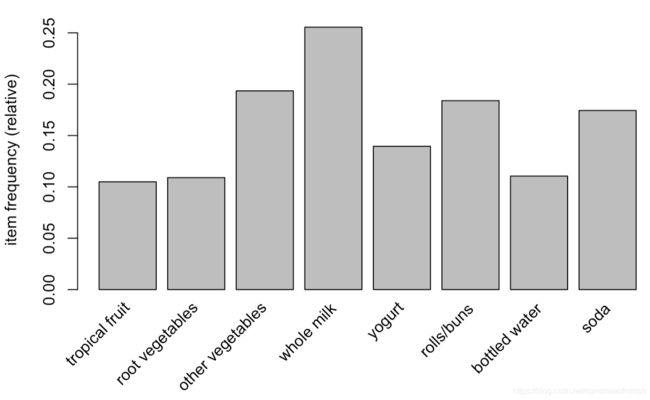
itemFrequencyPlot(Groceries, support=0.1) # 画出支持度为0.1情况下,频繁的项集的支持度
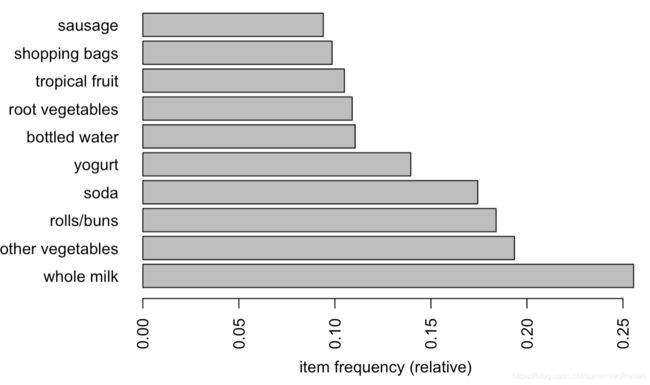
itemFrequencyPlot(Groceries, topN=10, horiz=T) # 排名前10频繁的项集的相对支持度
Apriori算法找频繁项集
itemsets_apr = apriori (Groceries,
parameter = list (supp = 0.001,target = "frequent itemsets"),
control = list(sort = -1))
# apriori函数参数默认值为:support=0.1,confidence=0.8,maxlen=10,minlen=1,target="rules"
# target = "frequent itemsets":找频繁项
# control中的参数控制:1.项的排序,sort = -1,是按照算法中某一指标(比如,此处根据结果看,项集是按support/项集频繁度排)从大到小排;2.报告进度,待研究
对于minlen,maxlen这里指规则的LHS和RHS的并集的元素个数。所以minlen=1,意味着 {} => {beer}是合法的规则。我们往往不需要这种规则,所以一般需要设定minlen=2。
## Apriori
##
## Parameter specification:
## confidence minval smax arem aval originalSupport maxtime support minlen
## NA 0.1 1 none FALSE TRUE 5 0.001 1
## maxlen target ext
## 10 frequent itemsets FALSE
##
## Algorithmic control:
## filter tree heap memopt load sort verbose
## 0.1 TRUE TRUE FALSE TRUE -1 TRUE
##
## Absolute minimum support count: 9
##
## set item appearances ...[0 item(s)] done [0.00s].
## set transactions ...[169 item(s), 9835 transaction(s)] done [0.00s].
## sorting and recoding items ... [157 item(s)] done [0.00s].
## creating transaction tree ... done [0.00s].
## checking subsets of size 1 2 3 4 5 6 done [0.01s].
## writing ... [13492 set(s)] done [0.00s].
## creating S4 object ... done [0.00s].
利用apriori算法发现Groceries中有13492个频繁项集。
inspect(itemsets_apr[1:5]) # 查看前5个频繁项集
## items support count
## [1] {whole milk} 0.2555160 2513
## [2] {other vegetables} 0.1934926 1903
## [3] {rolls/buns} 0.1839349 1809
## [4] {soda} 0.1743772 1715
## [5] {yogurt} 0.1395018 1372
support是相对支持度,count是支持度计数。
算法1:Apriori算法找频繁项集&关联规则
只有Apriori算法才能输出关联规则,eclat算法不能!
rules0 = apriori(Groceries,
parameter = list(support = 0.001,confidence = 0.5,maxlen = 3),
control = list(sort = -1))
# target的默认参数为"rules",故不用在parameter中特意写出,apriori函数就可以找关联规则
# maxlen规定了一条规则中,左项集和右项集包含项的总数不超过maxlen
## Apriori
##
## Parameter specification:
## confidence minval smax arem aval originalSupport maxtime support minlen
## 0.5 0.1 1 none FALSE TRUE 5 0.001 1
## maxlen target ext
## 3 rules FALSE
##
## Algorithmic control:
## filter tree heap memopt load sort verbose
## 0.1 TRUE TRUE FALSE TRUE -1 TRUE
##
## Absolute minimum support count: 9
##
## set item appearances ...[0 item(s)] done [0.00s].
## set transactions ...[169 item(s), 9835 transaction(s)] done [0.00s].
## sorting and recoding items ... [157 item(s)] done [0.00s].
## creating transaction tree ... done [0.00s].
## checking subsets of size 1 2 3 done [0.00s].
## writing ... [1472 rule(s)] done [0.00s].
## creating S4 object ... done [0.00s].
minsup=0.001,minconf=0.5的情况下,apriori函数找到了1472条强相关规则。
rules0
## set of 1472 rules
inspect(rules0[1:10]) # 查看前10条强相关规则
## lhs rhs support confidence
## [1] {baking powder} => {whole milk} 0.009252669 0.5229885
## [2] {rice} => {whole milk} 0.004677173 0.6133333
## [3] {cereals} => {whole milk} 0.003660397 0.6428571
## [4] {jam} => {whole milk} 0.002948653 0.5471698
## [5] {cooking chocolate} => {whole milk} 0.001321810 0.5200000
## [6] {pudding powder} => {whole milk} 0.001321810 0.5652174
## [7] {cocoa drinks} => {whole milk} 0.001321810 0.5909091
## [8] {honey} => {whole milk} 0.001118454 0.7333333
## [9] {specialty cheese} => {other vegetables} 0.004270463 0.5000000
## [10] {rice} => {other vegetables} 0.003965430 0.5200000
## lift count
## [1] 2.046793 91
## [2] 2.400371 46
## [3] 2.515917 36
## [4] 2.141431 29
## [5] 2.035097 13
## [6] 2.212062 13
## [7] 2.312611 13
## [8] 2.870009 11
## [9] 2.584078 42
## [10] 2.687441 39
lhs:左项集,rhs:右项集。
rules2 = apriori(Groceries,
parameter = list(support = 0.005,confidence = 0.64),
control = list(sort = -1))
rules2
inspect(rules2)
## lhs rhs support confidence lift count
## [1] {pip fruit,
## whipped/sour cream} => {whole milk} 0.005998983 0.6483516 2.537421 59
## [2] {butter,
## whipped/sour cream} => {whole milk} 0.006710727 0.6600000 2.583008 66
## [3] {pip fruit,
## root vegetables,
## other vegetables} => {whole milk} 0.005490595 0.6750000 2.641713 54
## [4] {tropical fruit,
## root vegetables,
## yogurt} => {whole milk} 0.005693950 0.7000000 2.739554 56
上面的sort是按照频繁度排序,下面可以按照其他指标(比如support)排序:
rules.sorted_sup = sort (rules2, by = "support")
inspect (rules.sorted_sup)
## lhs rhs support confidence lift count
## [1] {butter,
## whipped/sour cream} => {whole milk} 0.006710727 0.6600000 2.583008 66
## [2] {pip fruit,
## whipped/sour cream} => {whole milk} 0.005998983 0.6483516 2.537421 59
## [3] {tropical fruit,
## root vegetables,
## yogurt} => {whole milk} 0.005693950 0.7000000 2.739554 56
## [4] {pip fruit,
## root vegetables,
## other vegetables} => {whole milk} 0.005490595 0.6750000 2.641713 54
比如按confidence:
rules.sorted_con = sort (rules2, by = "confidence" )
inspect (rules.sorted_con)
## lhs rhs support confidence lift count
## [1] {tropical fruit,
## root vegetables,
## yogurt} => {whole milk} 0.005693950 0.7000000 2.739554 56
## [2] {pip fruit,
## root vegetables,
## other vegetables} => {whole milk} 0.005490595 0.6750000 2.641713 54
## [3] {butter,
## whipped/sour cream} => {whole milk} 0.006710727 0.6600000 2.583008 66
## [4] {pip fruit,
## whipped/sour cream} => {whole milk} 0.005998983 0.6483516 2.537421 59
比如按lift:
rules.sorted_lift = sort (rules2, by = "lift")
inspect (rules.sorted_lift)
## lhs rhs support confidence lift count
## [1] {tropical fruit,
## root vegetables,
## yogurt} => {whole milk} 0.005693950 0.7000000 2.739554 56
## [2] {pip fruit,
## root vegetables,
## other vegetables} => {whole milk} 0.005490595 0.6750000 2.641713 54
## [3] {butter,
## whipped/sour cream} => {whole milk} 0.006710727 0.6600000 2.583008 66
## [4] {pip fruit,
## whipped/sour cream} => {whole milk} 0.005998983 0.6483516 2.537421 59
找出某种特定商品的关联规则,利用apriori函数中的参数appearance来控制:
rules3 = apriori(Groceries,
parameter = list(maxlen = 2,supp = 0.001,conf = 0.1),
appearance = list(rhs = "mustard",default = "lhs"))
# supp是support的简写,conf是confidence的简写
# rhs = "mustard",右项集设定为芥末{mustard},如果商家想通过两件商品捆绑销售的方式来促销冷门商品芥末,我们需要发现rhs仅包含芥末的关联规则,从而找到与芥末强关联的商品
inspect(rules3)
## lhs rhs support confidence lift count
## [1] {mayonnaise} => {mustard} 0.001423488 0.1555556 12.96516 14
发现购买蛋黄酱的顾客更有可能购买芥末。
算法2:ECLAT算法找频繁项集
ECLAT算法只能用来找频繁项,不能用来找规则。
itemsets_ecl = eclat(Groceries,
parameter = list (minlen = 1, maxlen = 3,supp = 0.001, target = "frequent itemsets"),
control = list(sort = 1))
## Eclat
##
## parameter specification:
## tidLists support minlen maxlen target ext
## FALSE 0.001 1 3 frequent itemsets FALSE
##
## algorithmic control:
## sparse sort verbose
## 7 1 TRUE
##
## Absolute minimum support count: 9
##
## create itemset ...
## set transactions ...[169 item(s), 9835 transaction(s)] done [0.00s].
## sorting and recoding items ... [157 item(s)] done [0.00s].
## creating sparse bit matrix ... [157 row(s), 9835 column(s)] done [0.00s].
## writing ... [9969 set(s)] done [0.04s].
## Creating S4 object ... done [0.00s].
itemsets_ecl
## set of 9969 itemsets
inspect(itemsets_ecl[1:5])
有人发现ECLAT函数是自动滤去了频繁的一项集的,学有余力的朋友可以研究一下。
## items support count
## [1] {other vegetables,whole milk,cleaner} 0.001016777 10
## [2] {other vegetables,whole milk,curd cheese} 0.001220132 12
## [3] {other vegetables,whole milk,jam} 0.001321810 13
## [4] {other vegetables,whole milk,cereals} 0.001321810 13
## [5] {other vegetables,whole milk,kitchen towels} 0.001016777 10
interesting检验
通过interestMeasure函数实现
列联表检验/卡方检验
interestMeasure(rules2,measure = "chiSquared",transactions = Groceries,significance = T)
检验结果是4个强关联规则的列联表检验的p值。p值越小,越拒绝原假设,越说明关系是显著的。
## [1] 6.026803e-18 1.147537e-20 5.736532e-18 5.565073e-20
费希尔精确检验 Fishers Exact Test
是用于分析列联表(contingency tables)统计显著性检验方法,它用于检验两个分类关联(association)。虽然实际中常常使用于小数据情况,但同样适用于大样本的情况。费希尔精确检验是基于超几何分布计算的
原假设:没有显著相关关系。

例4
想知道颜值高(颜值评分仅为题目用假设,现实中不以长相论英雄,各有各的魅力)的人是不是数学成绩也好(单边检验),原假设:颜值跟成绩无显著相关性。
为了知道能否拒绝原假设,我们下面做个Fisher精确检验(单边检验)
第一步:想知道原假设是否成立,就要看这组数据是不是随机偶然一抽就能抽到,因此计算原假设成立时,即颜值高与颜值低的人,高分低分的数量相同时,得到这样一组数据的超几何概率:
p 1 = ( 12 9 ) ( 8 1 ) ( 20 10 ) p_1=\frac{\binom {12}{9} \binom {8}{1}}{\binom {20}{10}} p1=(1020)(912)(18)
第二步:做完上面这一步还不够。如果行总数与列总数(又叫边际总数)不变,原假设不成立时的极端情况应该是,颜值高的学习都好!那么我们可以得到新的列联表:
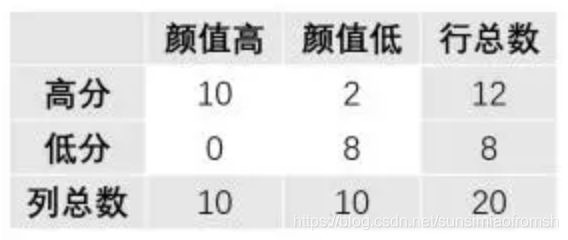
这时,可以计算这个表格的超几何概率,
p 2 = ( 12 10 ) ( 8 0 ) ( 20 10 ) p_2=\frac{\binom {12}{10} \binom {8}{0}}{\binom {20}{10}} p2=(1020)(1012)(08)
那么费希尔精确检验的p值就是两者加之和,即
p = p 1 + p 2 = 0.0099 p=p_1+p_2=0.0099 p=p1+p2=0.0099
p值越小,我们越有信心拒绝零假设。如果以0.05为显著性水平判断值的话,可以认为,颜值高的人,数学学得好。
interestMeasure(rules2,measure = "fishersExactTest",transactions = Groceries)
## [1] 2.784179e-15 1.545268e-17 3.167091e-15 7.433712e-17
可视化操作
arulesViz包中有arulesViz函数(可视化)。
rules4 = apriori (Groceries, parameter = list(support=0.002, confidence=0.5))
## Apriori
##
## Parameter specification:
## confidence minval smax arem aval originalSupport maxtime support minlen
## 0.5 0.1 1 none FALSE TRUE 5 0.002 1
## maxlen target ext
## 10 rules FALSE
##
## Algorithmic control:
## filter tree heap memopt load sort verbose
## 0.1 TRUE TRUE FALSE TRUE 2 TRUE
##
## Absolute minimum support count: 19
##
## set item appearances ...[0 item(s)] done [0.00s].
## set transactions ...[169 item(s), 9835 transaction(s)] done [0.00s].
## sorting and recoding items ... [147 item(s)] done [0.00s].
## creating transaction tree ... done [0.00s].
## checking subsets of size 1 2 3 4 5 done [0.00s].
## writing ... [1098 rule(s)] done [0.00s].
## creating S4 object ... done [0.00s].
可视化
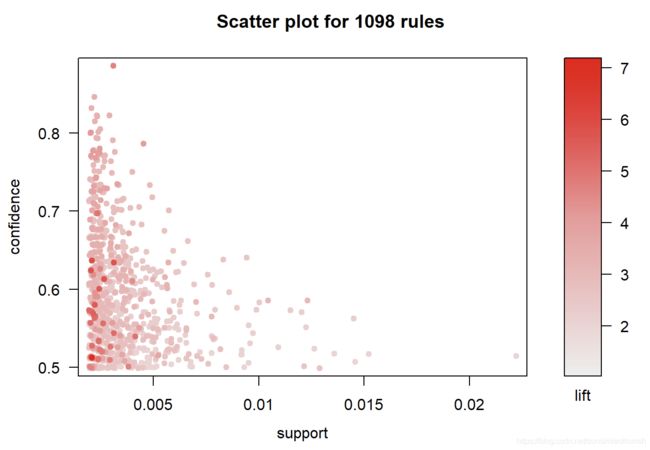
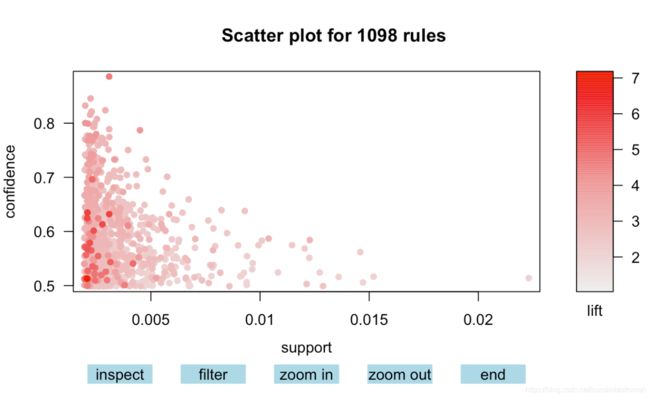
plot(rules4)
# 所有1098条关联规则的三维信息:支持度、置信度、lift值
plot(rules4, shading = "order",
control = list(main = "Two‐key plot"))
# 颜色深度代表关联规则中含有商品数量的多少
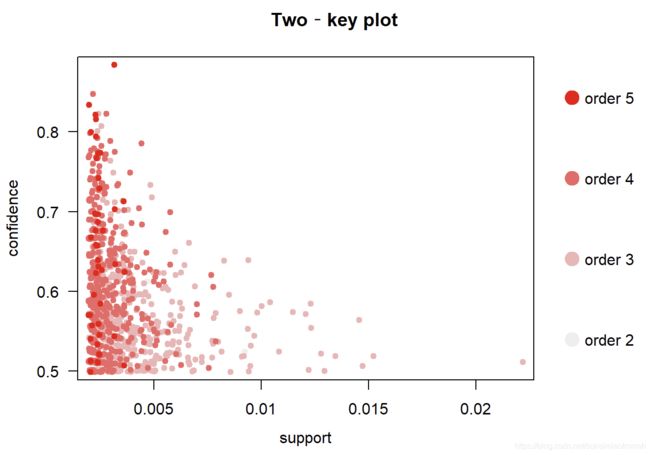
互动散点图,在R中运行才能看见,要点击图中右下角“End”才能停止图片运行,然后接着运行下面的代码。plot函数参数 engine=‘interactive’。
plot(rules4, engine='interactive')
基于图形的可视化,plot函数中参数method = “graph”
rules4.sorted <- sort(rules4,by="lift")
inspect(rules4.sorted[1:10])
## lhs rhs support confidence lift count
## [1] {butter,
## hard cheese} => {whipped/sour cream} 0.002033554 0.5128205 7.154028 20
## [2] {beef,
## citrus fruit,
## other vegetables} => {root vegetables} 0.002135231 0.6363636 5.838280 21
## [3] {citrus fruit,
## tropical fruit,
## other vegetables,
## whole milk} => {root vegetables} 0.003152008 0.6326531 5.804238 31
## [4] {citrus fruit,
## other vegetables,
## frozen vegetables} => {root vegetables} 0.002033554 0.6250000 5.734025 20
## [5] {beef,
## tropical fruit,
## other vegetables} => {root vegetables} 0.002745297 0.6136364 5.629770 27
## [6] {root vegetables,
## yogurt,
## bottled water} => {tropical fruit} 0.002236909 0.5789474 5.517391 22
## [7] {herbs,
## other vegetables,
## whole milk} => {root vegetables} 0.002440264 0.6000000 5.504664 24
## [8] {pip fruit,
## grapes} => {tropical fruit} 0.002135231 0.5675676 5.408941 21
## [9] {herbs,
## yogurt} => {root vegetables} 0.002033554 0.5714286 5.242537 20
## [10] {beef,
## other vegetables,
## soda} => {root vegetables} 0.002033554 0.5714286 5.242537 20
plot(rules4.sorted[1:10], method="graph")
plot(rules4.sorted[1:10], method="graph",engine='interactive')
利用关联规则做分类
采用computer数据做一个关联规则做分类的例子,computer数据如下:
computer
## age income student credit_rating buys_computer
## 1 youth high no fair no
## 2 youth high no excellent no
## 3 middle-aged high no fair yes
## 4 senior medium no fair yes
## 5 senior low yes fair yes
## 6 senior low yes excellent no
## 7 middle-aged low yes excellent yes
## 8 youth medium no fair no
## 9 youth low yes fair yes
## 10 senior medium yes fair yes
## 11 youth medium yes excellent yes
## 12 middle-aged medium no excellent yes
## 13 middle-aged high yes fair yes
## 14 senior medium no excellent no
# buys_computer是因变量
apriori算法找规则:
itemsets_apr = apriori (computer,
parameter = list (supp = 0.001,minlen = 1,maxlen = 3),
appearance = list(rhs = "buys_computer=yes",default = "lhs"),
control = list(sort = -1))
## Apriori
##
## Parameter specification:
## confidence minval smax arem aval originalSupport maxtime support minlen
## 0.8 0.1 1 none FALSE TRUE 5 0.001 1
## maxlen target ext
## 3 rules FALSE
##
## Algorithmic control:
## filter tree heap memopt load sort verbose
## 0.1 TRUE TRUE FALSE TRUE -1 TRUE
##
## Absolute minimum support count: 0
##
## set item appearances ...[1 item(s)] done [0.00s].
## set transactions ...[12 item(s), 14 transaction(s)] done [0.00s].
## sorting and recoding items ... [12 item(s)] done [0.00s].
## creating transaction tree ... done [0.00s].
## checking subsets of size 1 2 3 done [0.00s].
## writing ... [16 rule(s)] done [0.00s].
## creating S4 object ... done [0.00s].
看什么样的人倾向于买电脑。
itemsets_apr.sorted <- sort(itemsets_apr,by="lift")
inspect(itemsets_apr.sorted)
## lhs rhs support confidence lift count
## [1] {age=middle-aged} => {buys_computer=yes} 0.28571429 1.0000000 1.555556 4
## [2] {student=yes,
## credit_rating=fair} => {buys_computer=yes} 0.28571429 1.0000000 1.555556 4
## [3] {age=senior,
## credit_rating=fair} => {buys_computer=yes} 0.21428571 1.0000000 1.555556 3
## [4] {age=middle-aged,
## credit_rating=fair} => {buys_computer=yes} 0.14285714 1.0000000 1.555556 2
## [5] {income=low,
## credit_rating=fair} => {buys_computer=yes} 0.14285714 1.0000000 1.555556 2
## [6] {age=middle-aged,
## student=no} => {buys_computer=yes} 0.14285714 1.0000000 1.555556 2
## [7] {income=medium,
## student=yes} => {buys_computer=yes} 0.14285714 1.0000000 1.555556 2
## [8] {age=youth,
## student=yes} => {buys_computer=yes} 0.14285714 1.0000000 1.555556 2
## [9] {income=high,
## student=yes} => {buys_computer=yes} 0.07142857 1.0000000 1.555556 1
## [10] {age=middle-aged,
## student=yes} => {buys_computer=yes} 0.14285714 1.0000000 1.555556 2
## [11] {age=middle-aged,
## credit_rating=excellent} => {buys_computer=yes} 0.14285714 1.0000000 1.555556 2
## [12] {age=middle-aged,
## income=medium} => {buys_computer=yes} 0.07142857 1.0000000 1.555556 1
## [13] {age=youth,
## income=low} => {buys_computer=yes} 0.07142857 1.0000000 1.555556 1
## [14] {age=middle-aged,
## income=high} => {buys_computer=yes} 0.14285714 1.0000000 1.555556 2
## [15] {age=middle-aged,
## income=low} => {buys_computer=yes} 0.07142857 1.0000000 1.555556 1
## [16] {student=yes} => {buys_computer=yes} 0.42857143 0.8571429 1.333333 6
增加confidence=0.2条件
itemsets_apr2 = apriori (computer,
parameter = list(supp = 0.001,confidence = 0.2,minlen = 1,maxlen = 3),
appearance = list(rhs = "buys_computer=no",default = "lhs"),
control = list(sort = -1))
## Apriori
##
## Parameter specification:
## confidence minval smax arem aval originalSupport maxtime support minlen
## 0.2 0.1 1 none FALSE TRUE 5 0.001 1
## maxlen target ext
## 3 rules FALSE
##
## Algorithmic control:
## filter tree heap memopt load sort verbose
## 0.1 TRUE TRUE FALSE TRUE -1 TRUE
##
## Absolute minimum support count: 0
##
## set item appearances ...[1 item(s)] done [0.00s].
## set transactions ...[12 item(s), 14 transaction(s)] done [0.00s].
## sorting and recoding items ... [12 item(s)] done [0.00s].
## creating transaction tree ... done [0.00s].
## checking subsets of size 1 2 3 done [0.00s].
## writing ... [30 rule(s)] done [0.00s].
## creating S4 object ... done [0.00s].
看什么样的人倾向于不买电脑。
itemsets_apr2.sorted <- sort(itemsets_apr2,by="lift")
inspect(itemsets_apr2.sorted)
## lhs rhs support confidence lift count
## [1] {age=youth,
## student=no} => {buys_computer=no} 0.21428571 1.0000000 2.8000000 3
## [2] {age=senior,
## credit_rating=excellent} => {buys_computer=no} 0.14285714 1.0000000 2.8000000 2
## [3] {income=high,
## credit_rating=excellent} => {buys_computer=no} 0.07142857 1.0000000 2.8000000 1
## [4] {age=youth,
## income=high} => {buys_computer=no} 0.14285714 1.0000000 2.8000000 2
## [5] {age=youth,
## credit_rating=fair} => {buys_computer=no} 0.14285714 0.6666667 1.8666667 2
## [6] {student=no,
## credit_rating=excellent} => {buys_computer=no} 0.14285714 0.6666667 1.8666667 2
## [7] {income=high,
## student=no} => {buys_computer=no} 0.14285714 0.6666667 1.8666667 2
## [8] {age=youth} => {buys_computer=no} 0.21428571 0.6000000 1.6800000 3
## [9] {student=no} => {buys_computer=no} 0.28571429 0.5714286 1.6000000 4
## [10] {credit_rating=excellent} => {buys_computer=no} 0.21428571 0.5000000 1.4000000 3
## [11] {income=high} => {buys_computer=no} 0.14285714 0.5000000 1.4000000 2
## [12] {student=no,
## credit_rating=fair} => {buys_computer=no} 0.14285714 0.5000000 1.4000000 2
## [13] {income=medium,
## student=no} => {buys_computer=no} 0.14285714 0.5000000 1.4000000 2
## [14] {age=senior,
## student=no} => {buys_computer=no} 0.07142857 0.5000000 1.4000000 1
## [15] {age=youth,
## credit_rating=excellent} => {buys_computer=no} 0.07142857 0.5000000 1.4000000 1
## [16] {income=low,
## credit_rating=excellent} => {buys_computer=no} 0.07142857 0.5000000 1.4000000 1
## [17] {age=youth,
## income=medium} => {buys_computer=no} 0.07142857 0.5000000 1.4000000 1
## [18] {age=senior,
## income=low} => {buys_computer=no} 0.07142857 0.5000000 1.4000000 1
## [19] {age=senior} => {buys_computer=no} 0.14285714 0.4000000 1.1200000 2
## [20] {} => {buys_computer=no} 0.35714286 0.3571429 1.0000000 5
## [21] {income=medium} => {buys_computer=no} 0.14285714 0.3333333 0.9333333 2
## [22] {income=medium,
## credit_rating=fair} => {buys_computer=no} 0.07142857 0.3333333 0.9333333 1
## [23] {income=high,
## credit_rating=fair} => {buys_computer=no} 0.07142857 0.3333333 0.9333333 1
## [24] {student=yes,
## credit_rating=excellent} => {buys_computer=no} 0.07142857 0.3333333 0.9333333 1
## [25] {age=senior,
## student=yes} => {buys_computer=no} 0.07142857 0.3333333 0.9333333 1
## [26] {income=medium,
## credit_rating=excellent} => {buys_computer=no} 0.07142857 0.3333333 0.9333333 1
## [27] {age=senior,
## income=medium} => {buys_computer=no} 0.07142857 0.3333333 0.9333333 1
## [28] {credit_rating=fair} => {buys_computer=no} 0.14285714 0.2500000 0.7000000 2
## [29] {income=low} => {buys_computer=no} 0.07142857 0.2500000 0.7000000 1
## [30] {income=low,
## student=yes} => {buys_computer=no} 0.07142857 0.2500000 0.7000000 1
说明&致谢
本人第一次书写机器学习笔记,仓促草率,其中多有不妥,欢迎也感谢各位学习者到评论区指出文中问题。在此,特要感谢本人机器学习的授课老师Ms.L提供的资料和教学。Come and Join Us Machine Learning!
接下来计划基于python/SAS语言学习关联分析,并书写读书笔记。
参考资料
Jiawei Han, Micheline Kamber, Jian Pei(2012). Data Mining Concepts and Techniques.
https://doi.org/10.1016/C2009-0-61819-5. ↩︎Xindong Wu, Vipin Kumar(2009). The Top Ten Algorithms in Data Mining. ↩︎
版权声明:本文为CSDN博主「gjwang1983」的原创文章,遵循 CC 4.0 BY-SA 版权协议,转载请附上原文出处链接及本声明。原文链接:https://blog.csdn.net/gjwang1983/article/details/45015203. ↩︎
https://www.jianshu.com/p/f0e1b0100e59. ↩︎