求最长回文串-从动态规划到"马拉车"之路(上)
要解决的问题:
给定一个字符串,要求求出这个字符串中的最长的回文串子串。
例子:
cbddba的最长回文子串为 bddb
cbdedba的最长回文子串为dbedb
由上面的例子可以看到,在考虑回文子串的问题时需要考虑奇偶性。因为奇回文关于中心的某个字符对称,而偶回文关于最中心的两个元素之间的间隙对称。
一、动态规划法
在动态规划的思想中,总是希望把问题划分成相关联的子问题;然后从最基本的子问题出发来推导较大的子问题,直到所有的子问题都解决。
首先要看一个较大的子问题与一个较小的子问题之间的关系:
首先建立如下的函数:
那么就能有如下的递推关系:
当p(i+1,j-1) = true 的时候,如果有si == sj,那么 p(i,j)=true;也就是 abba中的bb为回文串,那么在bb左边是a,在bb右边也是a,相同;所以有abba也是回文串。
形式化表示如下: p(i,j) = p(i+1,j-1) and si==sj 这就建立了较大问题与较小问题之间的关系。
然后考虑基本情况,一个最基本的回文串有两种情况(奇偶性):
(1) 最基本的奇回文,只有一个字符,而且恒成立;形式化表示为 p(i,i) = true
(2)最基本的偶回文,有两个字符,当且仅当两个字符相等的时候成立p(i,j) = (si==sj and j=i+1)
最后获得如下判断一个字符是否为回文串的分段函数:
有了公式,就是用代码实现了;下面给出了我的python实现。
# -*- coding:utf-8 -*-
# Author: Evan Mi
# 测试的字符串
str_exp = "babad"
# 用来保存动态规划过程的表 1表示true 0表示false
longest_palindromes = [[-1] * len(str_exp) for i in range(len(str_exp))]
# longest_len 用来保存最长的回文串的长度
longest_len = 1
# 从长度为1的回文子串开始填表
for p_len in range(1, len(str_exp)+1):
for i in range(len(str_exp)):
j = p_len + i - 1
if j < len(str_exp):
if i == j:
longest_palindromes[i][j] = 1
elif j == i + 1 and str_exp[i] == str_exp[j]:
longest_palindromes[i][j] = 1
longest_len = p_len
elif j > i+1 and longest_palindromes[i+1][j-1] == 1 and str_exp[i] == str_exp[j]:
longest_palindromes[i][j] = 1
longest_len = p_len
else:
longest_palindromes[i][j] = 0
# 搜索结果表,打印出所有的最优解
for i in range(len(str_exp)):
for j in range(len(str_exp)):
if longest_palindromes[i][j] == 1 and j-i+1 == longest_len:
print(str_exp[i:j+1])在动态规划中,最最最核心的就是填表了,就以程序中的例子"babad"举例,说明一下填表的过程;
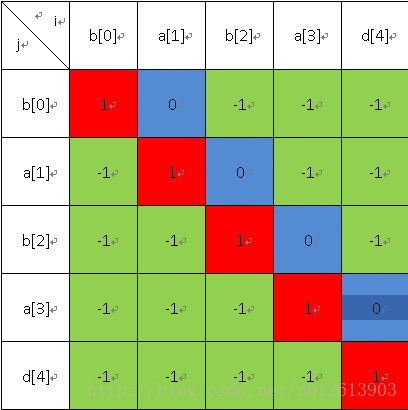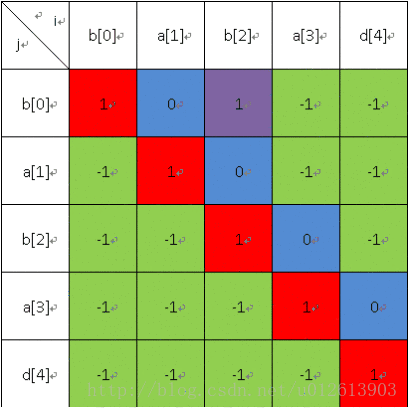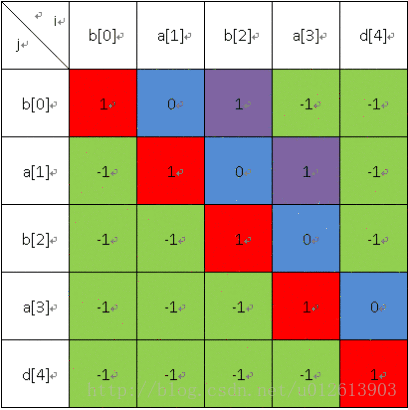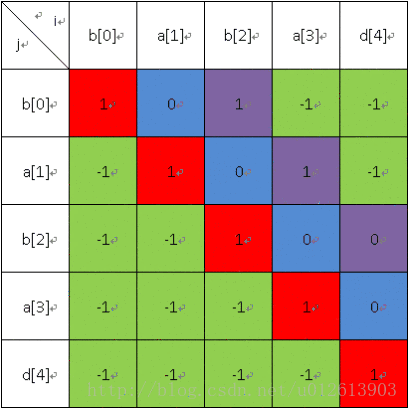
首先我们要填的表是如下的一张表二维表(因为p函数中有i,j两个变量),其中绿色的部分是真实的表格,其他的是我家的解释表头。
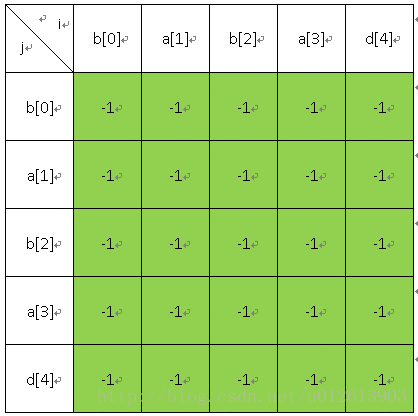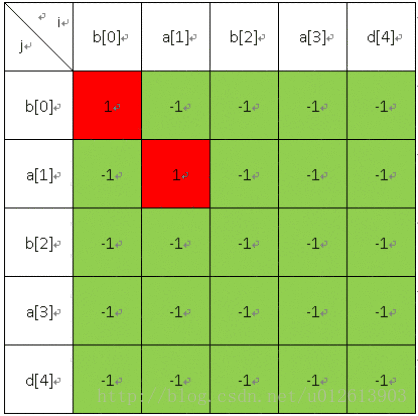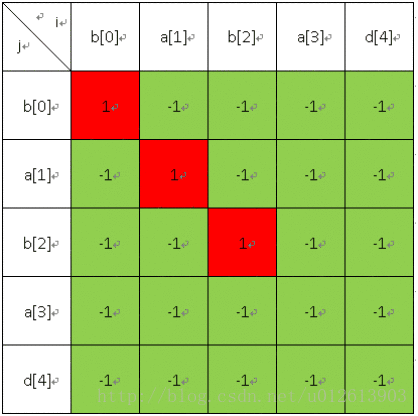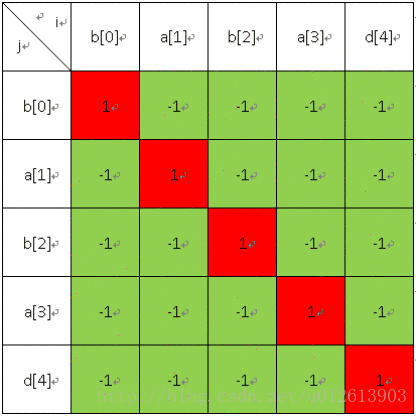
填表过程如下:首先填长度为1的;
然后填长度为2的;
接着是长度为3的:
长度为4的:
最后是长度为5的:
填表完成之后,求最优解就是查询了;对于时间复杂度,动态规划的时间复杂度在构建表的过程中的基本操作,所以时间复杂度是O(n^2);空间复杂度,就是上面的二维数组,也是O(n^2)。而且从在空间浪费(主对角线下面的空间没有使用,浪费了一般的空间)。有很多针对空间上的优化方法,下面给出一种空间复杂度为O(1)的算法;
二、空间复杂度为O(1)的算法
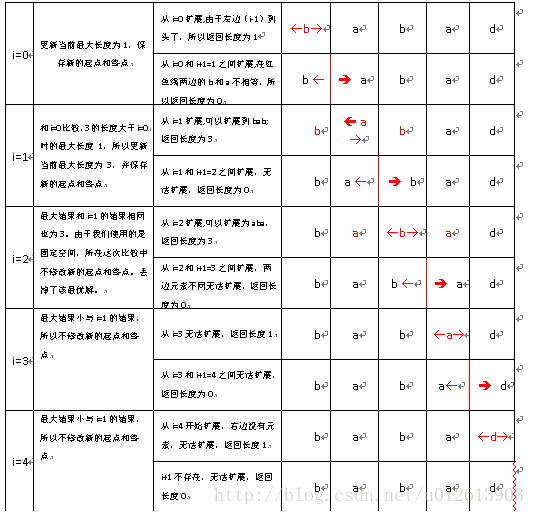
该算法的主要思想就遍历所有的字符(下标为i)是以第i个数(对应奇回文)或者第i个数和第i+1个数之间的间隙(对应偶回文)为中心向两边扩展,直到扩展以后不再是回文,那么就停止扩展,如果回文长度比已知的最长回文长,那么记录下该回问的开始位置和结束位置为最长回文;
还是用"babad"来作为例子,过程如下:
代码实现如下:
# -*- coding:utf-8 -*-
# Author: Evan Mi
import math
def expandAroundCenter(left, right, s):
"""
从left和right之间开始扩展,如果left==right
就是以left/right为中心进行扩展
"""
rLeft = left
rRight = right
while rLeft >= 0 and rRight < len(s) and s[rLeft] == s[rRight]: # 进行扩展
rLeft -= 1
rRight += 1
"""
针对于返回的长度,因为在while循环停止的时候,rLeft和rRight都已经在要求的回文串之外了
所以回文串的长度为rRight - rLeft - 1,自己可以画个过程图,一目了然。
"""
return rRight - rLeft - 1
s = "babad"
start = 0
end = 0
for i in range(len(s)):
odd_len = expandAroundCenter(i, i, s) # i为中心的扩展
even_len = expandAroundCenter(i, i + 1, s) # i 和 i+1之间的空隙为中心进行扩展
lens = max(odd_len, even_len) # 取得本次扩展的最大值
if lens > (end-start+1): # 如果本次的长度比记录的回文的长度也就是end-start+1大,进行替换
# 需要注意的是,已经知道了位置i,不管是以i为中心扩展了长为lens的回文还是
# 以i和i+1的空隙为中心扩展了长为lens的回文。下面的start和end的计算方法都成立
start = i - math.floor((lens - 1) / 2)
end = i + math.floor(lens/2)
print(start, ":", end)
print(s[start:end+1])
这两个算法不论在空间、结果上有什么不同,它们的时间复杂度都是相同的;接下来就分析一下“马拉车”算法,该算法把时间复杂度降到了线性范围内。额,请见下篇博客。
PS:很多人都分析了"马拉车"算法,但是也阻挡不了我征服它的步伐。相信自己对它一定有独到的见解。