LeetCode之路：108. Convert Sorted Array to Binary Search Tree

一、引言

真是很久很久没有刷 LeetCode 了呢！

自从掉入了 Cef3 的坑之后，又加上期间看完了 《COM技术内幕》之后，又看了点《C++语言的设计和演化》，仿佛都将刷 LeetCode 这件事甩到脑后去了。虽然看书能够很好的提升自己，但是刷题也不失为一种雅兴。

不得不说，这道题还是挺有趣的，看看原题吧：

Given an array where elements are sorted in ascending order, convert ti to a height balanced BST.

这道题的描述如此简略，简单翻译下：

给定一个内部元素按照升序排列的数组，请将其转化成高度平衡的二叉搜索树。

这道题涉及到了一个非常重要的概念：二叉搜索树（Binary Search Tree）。

这里我找到了百度百科对于二叉搜索树的解释：

二叉查找树（Binary Search Tree），（又：二叉搜索树，二叉排序树）它或者是一棵空树，或者是具有下列性质的二叉树：若它的左子树不空，则左子树上所有结点的值均小于它的根结点的值；若它的右子树不空，则右子树上所有结点的值均大于它的根结点的值；它的左、右子树也分别是二叉排序树。

这里将二叉搜索树的性质讲述的非常清楚了，还需要注意的是，”height balanced BST”，也就是高度平衡的二叉搜索树，这里我又找到了平衡二叉树的定义：

平衡二叉树（Self-Balancing Binary search Tree）又被称为 AVL 数，且具有以下性质：它是一棵空树或它的左右两个子树的高度差的绝对值不超过1。

也就是说，综上所述，题目要求要转换成的二叉树是一种什么样的二叉树呢？以下举个例子说明：

Input: [1, 2, 3, 4, 5]
Output: [3,2,5,1,null,4]

看向上图，我们大概可以理解到高度平衡的二叉搜索树的含义了吧：

1. 任何一个结点的左子结点都小于它的值，右子结点都大于或者等于它的值

2. 任何一个结点的左子树和右子树的高度差绝对值小于或等于 1

那么，我们该如何做到从类似 [1, 2, 3, 4, 5] 的数组到这么一个高度平衡的二叉搜索树的转换的呢？

二、分析：我们在手动转换的时候在思考什么

想要分析这个问题，最简单的方法就是找到一个具体实例，然后我们用自己的思维方式（区别于程序思维）去实现一次。

那么这里已经有了一个实例了，也就是从 [1, 2, 3, 4, 5] 到上述引言中那个图示树的转换。

那么让我们脱离程序思维来看看作为一个“人”我们是怎么转换的：

1. 找到“最中间”的位置取一个根结点：为了确保高度差绝对值小于等于 1，我们需要找到最中间的位置取根结点，于是这里就取出了 3

2. 以根结点为中心，划分从数组开始到根结点结束的左侧数组（根结点的左子树数据），以及从根结点开始到原数组结束为止的右侧数组（根结点的右子树数据）。于是，这里出现的左子树数组就是 [1, 2]，右子树数组就是 [4, 5]

3. 我们重复第 1 步的操作，在左子树数组中找到了我们认为的“最中间”的位置 ；然后我们又重复了第 2 步的操作，将该左子树数组划分成了左右两个数组。于是，这里我们取到的第二个根结点就是 [2] （为什么这里是取 2 而非 1 待会儿解释），划分出来的左右数组为 [1] []

4. 我们一直这样重复下去，依次构造结点的左右子结点指针指向，直到所有的元素都被我们取完结束，此时也就构造出来了被转换成功的高度平衡的二叉搜索树了

在上面这个过程中，我们遗留了一个很重要的问题。那就是什么才能叫做“最中间”的元素：如果数组个数为奇数，那当然是取中间的那个；那如果为偶数呢？此时该取左边那个还是右边那个呢 T_T

这个问题非常非常重要，以至于我又找到了另一个实例进行分析：

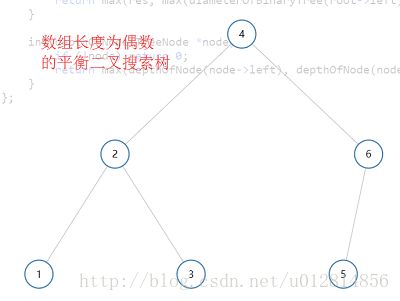
Input: [1, 2, 3, 4, 5, 6]
Output: [4,2,6,1,3,5]

你或许会说，我取 3 也是可以的，但是这就是这道题的 Expected Answer 我也没办法 T_T

也就是说，按照这道题的期待输出，在偶数的时候，我们取二分之后的靠右的那个元素是最合理的。

因此，我们总结出来了这么几点有助于我们之后的程序设计：

1. 只有 nums.size() / 2 的位置才是我们要取的根结点的位置（nums 数组的长度除以 2，正好是居中元素的下标位置）

2. 我们可以使用递归方式解题（涉及到循环取根结点、划分左右数组的单元操作）

三、实现：关于 C++ 语法的一点点思考

按照上述的分析，我很快就写出了下列的代码：

// my solution , runtime = 19 ms
class Solution {
public:
    TreeNode* sortedArrayToBST(vector<int>& nums) {
        if (nums.size() == 0) return nullptr;
        int mid = nums.size() / 2;
        TreeNode *node = new TreeNode(nums[mid]);
        auto leftTree = vector<int>(nums.begin(), nums.begin() + mid);
        auto rightTree = vector<int>(nums.begin() + mid + 1, nums.end());
        if (mid != 0)
            node->left = sortedArrayToBST(leftTree);
        if (mid != nums.size() - 1)
            node->right = sortedArrayToBST(rightTree);
        return node;
    }
};

这份代码成功 Accepted 了，这里还是简单分析下代码：程序一开始，判断当前数组是否为空，为空的话则直接返回空指针；之后创建一个 TreeNode 指针用来操作当前根结点；再之后根据根结点位置划分左右数组，再进行递归。

代码逻辑还是很简单的，但是我这里有个疑惑，不知道大家有没有注意到这两行代码：

auto leftTree = vector<int>(nums.begin(), nums.begin() + mid);
auto rightTree = vector<int>(nums.begin() + mid + 1, nums.end());

这两行代码声明了两个临时变量 leftTree 和 rightTree，然后之后又在递归调用本函数的时候传入了这两个参数。那么问题来了，作为一个代码简化强迫症患者，这里的两个临时变量可否删除，直接将 vector 对象构造在传参中呢？也就是说整份代码修改如下：

TreeNode* sortedArrayToBST(vector<int>& nums) {
    if (nums.size() == 0) return nullptr;
    int mid = nums.size() / 2;
    TreeNode *node = new TreeNode(nums[mid]);
    // auto leftTree = vector(nums.begin(), nums.begin() + mid);
    // auto rightTree = vector(nums.begin() + mid + 1, nums.end());
    if (mid != 0)
        node->left = sortedArrayToBST(vector<int>(nums.begin(), nums.begin() + mid));
    if (mid != nums.size() - 1)
        node->right = sortedArrayToBST(vector<int>(nums.begin() + mid + 1, nums.end()));
    return node;
}

我们 Run Code 一下，发现提示错误：

Line 19: invalid initialization of non-const reference of type 'std::vector&' from an rvalue of type 'std::vector'

这是什么意思呢？也就是说我们的传参并不满足其 sortedArrayToBST 函数的调用要求。

那么，我们有没有一种机制，在只完成了构造但并未赋值给某个具体变量的情况下就获取到这个对象的引用呢（也就是说我们完成了 constructor 但并未 assignment ，想要获取到对象的 reference 是否可行呢）

我查询了很多资料，答案是比较遗憾的，这是不行的，为什么不行呢？

C++ 的临时对象是不能赋值给引用的

为什么不能呢？

让我们来思考下赋值操作除了给一处空间声明了一个名字，还做了什么事情。

对呀，隐含着定义了这个对象的生命周期。也就是说，我们在无法定义一个对象的生命周期（生命周期意味着编译器知道该对象什么时候可以析构删除）的时候，就无法拿到它的引用，这是合理的。

四、总结

或许有些人会奇怪，这一篇博客里我居然不分析下最高票答案。我粗略看了下最高票答案，其实思路都是差不多的，也就没有再深入探讨了。

有关二叉树相关的问题，我们总会有一个非常给力的工具：递归。在仔细分析之后，往往使用递归能够大大简化我们的程序设计工作。

真的是好久没有刷 LeetCode 了，都觉得有些手生了。最近除了看了些 C++ 相关的书，还在自学 《Head First Python》英文版，这也是我第一本纯英文自学的教材，目前已经看到了 35% 了，感觉还是比较轻松的，希望自己能够坚持下来吧 ^_^

最后，LeetCode 之路还是会继续前行的，所谓学习与练习两者都需要兼顾：）

To be Stronger!