Manacher's Algorithm 马拉车算法

算法课的作业，每个组需要讲解一个经典问题和解决方案，同组的同学想讲这个，发给了我一些资料，此文仅作自己的理解过程的一个记录，如有错误之处请指教。

问题

经典的最长回文子串问题(Longest_palindromic_substring)。回文串就是正读反读都一样的字符串，比如 “a”,“bob”, “noon” 等。最长回文子串问题即在一个字符串中找出其长度最大的回文子串（这不废话嘛）。

传统解决方案

那么如何找呢，当然可以遍历每个字符，分别以其为中心，向两边寻找最长回文子串，遍历完整个数组后，就可以找到最长的回文子串。但是这个方法的时间复杂度为O(n²)，这简直是乌龟拉车，贼慢。

那马拉车呢？

这个算法一共有以下几步。

积偶合并

如上文，"bob"和"noon"都是回文字符，显然需要分情况讨论，而马拉车算法的第一步就是用一种添加字符的方法,在每一个字符的左右都添加上#号，把两种情况合并了。举例如下:
bob ——> #b#o#b#
noon ——> #n#o#o#n#
这样，添加字符后整个字符串一定是奇数（不信你自己查下）

我们需要用一个半径数组p[i]来 找长度 和 找位置

• 首先，在用#号处理字符前，如果知道了分别以每个字符为中心的最长回文串的半径，就可以得到最大的半径，从而可以得到最后的最长回文子串长度了。即这个半径与回文子串长度是有对应关系的。那么对按照固定方法（有规律的加#号）处理后的字符串，同样求出每个字符的新半径时，显然也可以对应到真实的回文子串长度。举个例子：
  “bob"中p[0] (以b为中心) 是1，p[1] (以o为中心)是2，p[2] (以b为中心) 是1.
  所以以b为中心的最长子串就是21-1=1，以o为中心的最长子串是22-1=3，以第二个b为中心的最长子串也是2*1-1=1。
  这就是对应关系。
  而对处理后的字符串”#b#o#b#"，其对应的p[]就是{1,2,1,4,1,2,1}
  那新的对应关系呢？我们来看，#号实际不存在，所以以其为中心的真实的回文子串长度是0，所以每个字符的最长回文子串长度数组应该是{0,1,0,3,0,1,0}，做下对比，其实就是p里面的数全部减了1，其实数学上很容易证明，也很容易想明白，前面是用半径对应的，现在的半径里相当于加了半径的#号个数直接变成长度了，又算了两遍自己什么的，好好想想很容易想明白。
• 光找到长度不行啊，还得知道从哪开始的啊，就是定位，定位才能把最后的最长回文子串找到。这里处理前的规则特别简单，位置i的字符半径如果是r，那i-r+1就是开始的字符的位置。处理后自然也有一个对应规则，不过这个规则经过了一些处理，具体规则肯定是经过马拉车先生自己试出来的，想了解过程的我给你们复制下来。。其实就是试。

我们还是先来看中间的 ‘1’ 在字符串 “#1#2#2#1#2#2#” 中的位置是7，而半径是6，貌似7-6=1，刚好就是回文子串 “22122” 在原串 “122122” 中的起始位置1。那么我们再来验证下 “bob”，“o” 在 “#b#o#b#” 中的位置是3，但是半径是4，这一减成负的了，肯定不对。所以我们应该至少把中心位置向后移动一位，才能为0啊，那么我们就需要在前面增加一个字符，这个字符不能是井号，也不能是s中可能出现的字符，所以我们暂且就用美元号吧，毕竟是博主最爱的东西嘛。这样都不相同的话就不会改变p值了，那么末尾要不要对应的也添加呢，其实不用的，不用加的原因是字符串的结尾标识为’\0’，等于默认加过了。那此时 “o” 在 “$ #b#o#b#” 中的位置是4，半径是4，一减就是0了，貌似没啥问题。我们再来验证一下那个数字串，中间的 ‘1’ 在字符串 “$ #1#2#2#1#2#2#” 中的位置是8，而半径是6，这一减就是2了，而我们需要的1，所以我们要除以2。之前的 “bob” 因为相减已经是0了，除以2还是0，没有问题。再来验证一下 “noon”，中间的 ‘#’ 在字符串 “$#n#o#o#n#” 中的位置是5，半径也是5，相减并除以2还是0，完美。可以任意试试其他的例子，都是符合这个规律的.

规律就是在加了#号的字符串前面加个符号，比如上文的$（后面没加所以每个回文串的长度不会变），最长子串的长度是最大半径减1，起始位置是中间位置减去半径再除以2。 感受感受，其实也很容易理解，加#号相当与加了一倍（还少1），加了个 $ 号相当于刚好补成两倍长，剪了新半径相当于减了自己的长度，然后再放缩（缩）回1/2就是起始位置了。

怎么把这个p[i]搞出来？

暴力循环？那不还是之前的方法，得想个好办法啊，怎么想呢？我怎么知道，马拉车想出来的，我看完只想说，果然聪明。。
p[i] = mx > i ? min(p[2 * id - i], mx - i) : 1;
what’s this?

what’s 又 this?

刚开始我也看的很晕，别急。
首先，搞清楚我们要干啥，求p[i]！
mx又是什么？ 离i最近的回文子串的右端
那id是什么？ 上面说的那个最近的子串的中心
请注意，不需要它长，只需要它近！当然又近又长最好，但是近优先度高于长。
至于原因也很简单，就是要用这个子串内部的对称方便求p[i]，那肯定是离i越近的子串越好啊。
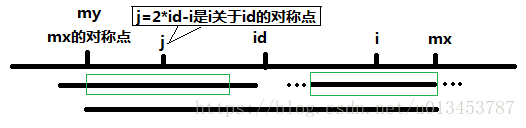
哪来的j？？？ 创造的啊！，j=2*id-i ,那(i+j)/2不就是id么！i关于id的对称点懂么？通过对称的特性来简化求p[i]啊！
心累，那这个表达式又又又表达了什么逻辑？？ 利用id、mx、j 简化求p[i]啊
首先问mx大于i么？如果mx大于i，其实i就是被笼罩在目前的回文子串里，那有什么特点？i和j这两个对称点情况差不多啊。
如果mx-i>=p[j]，意思就是回文子串完全把j的最长回文子串笼罩住了啊，那还不简单，p[i]也肯定被完全笼罩著了，而且跟p[j]一模一样。
举个例子就是 madabadam里，这个到b的时候回文子串已经是全部了，最右边mx就是最右边那个m了，它已经笼罩了左边那个d的最长回文子串（ada），所以右边那个d的p值跟左边那个d肯定一样啊，因为对称(它也是ada)呗。感觉我说的已经很清楚了，还是上一下人家的图吧。

那mx>i但是mx-i<=p[j]呢，简单来说就是笼罩了一部分，就是说j的最长子串都超过id的子串的左边了，那很明显i的最长子串也可能超过id子串的右边啊，但最起码p[i]得刚刚好是mx-i吧，至于更多的，谁知道呢？那怎么办？我先让p[i]=mx-i，然后从mx-i那么长继续往外暴力啊，这都已经省了不少事了。（有些问题，在文章最后重新更正,请看更正2）上一下人家的图。

最后，要是mx<=i呢？（=号的问题在最后说明了！请看更正1） id的子串跟i都没关系，我咋简化p[i]，鞭长莫及啊，老老实实从1暴力~
这就是整个这段代码的意思。

核心逻辑搞明白之后，再想想这个思路到底是啥？这不就是想办法搞了个动态规划么？通过记录离目标最近的回文子串的中点和最右边的点，通过对称，把i对称到j，然后就可以用已经求过了的p[j]简化p[i]的算法（三种情况，要么直接不用算了，要么直接在p[j]上继续算，要么还是得从头算）。

搞完p[i]出答案完事

前面说了咋操作

Code

准备健身去，待会回来写…

package manacher;

public class Manacher {
	public static String Manacher(String s) {
		if (s == "") return "";
		//1.加#
		
		//t是目的字符数组
		String t ="$#";
		for(int i = 0 ; i < s.length(); i++) {
			t += s.charAt(i);
			t += "#";
		}
		//防止越界
		t += '0';		
		//2.迭代求p
		
		//p[]记录每个点为中心的最大回文子串
		int[] p =new int[t.length()];
		//id为能延伸到最右边的（为了多让后面的计算能用到）的那个回文子串的中心，mx为它的最右，区间为[...,mx) 而不是 [...,mx] 所以下面的判断是>号！
		int id = 0, mx = 0;
		//resLen为当前最长字串长度，resCenter当前最长字串中心
		int resLen = 0, resCenter = 0;
		//从1循环是p[0]一定是1,因为t[0]是$
		
		
		for(int i = 1; i < t.length() - 1; i++) {
			p[i] = mx > i ? Math.min(p[2 * id - i], mx - i) : 1;
			//只有在两种情况下继续迭代
			
			  while (((i - p[i]) >= 0) && ((i + p[i]) < t.length()-1) && (t.charAt(i + p[i]) == t.charAt(i - p[i]))) {
				p[i]++;	
			}
			if(mx < i + p[i]) {
				mx = i + p[i];
				id = i;
			}
			if(resLen < p[i]) {
				resLen = p[i];
				resCenter = i;
			}
		}
		//按规则返回 
		//注意C++和java的substring
		return s.substring((resCenter - resLen) / 2, (resCenter - resLen) / 2 + resLen - 1);
	}
	public static void main(String[] args) {
		
		String s1 = "abcbad";
		String s2 = "dabcba";
		String s3 = "a";
		String s4 = "";
		String s5 = "skdjfkdsncvnskddjfkdfkdsjfkdfdsfdsfs";
		String[] s = {s1, s2, s3, s4, s5};
		for(String str : s) {			
			System.out.println(Manacher(str));
		}
		//System.out.println(Manacher(s3));
				
	}
}

补！

昨天躺在床上的时候又想了一下，更正几点：

更正1. mx是最右边的回文子串的最右边，但是是 “)”而不是“]”，请仔细体会，如$#a#b#a#中，i=2时为a，其p[i]最后算出是2，2+2=4，4是b的位置，a的最长回文子串是#a#，其实不到b。 那么在判断b的时候，问的是mx>i么？意思就是 mx = i 的时候 其实也没覆盖到。这一点其实是对a本身自己一个，甚至 $的 p都是1的一个变通，只有这样逻辑才是对的。

更正2. 上文对mx-i<=p[j]的讨论中出现了一些不清晰，仔细思考了之后发现了马拉车算法的真正强大的地方。

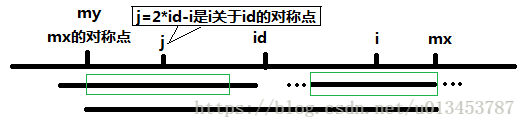
仔细思考关于id的对称，如果mx-i 这里就先不加#号和 $号那些了，那些只是辅助合并积偶情况的，对算法的理解不影响，如babeba中，在对i=5的c进行求p时，显然id=3,mx=6,那么mx-i =1;j为c关于e对称的位置，即j=1，p[j]=2。
满足 mx-i 按照之前的规则，我们会先把p[i]设置为mx-i也就是1，然后继续扩张。
问题是我们需要继续扩张么？
或者说我们扩张的判断到底有可能成功么？？？
我们在回头看看这个字符串，babeba中，左边的a和右边的a对称，而ab和ba又关于e对称，假设我们右边的a，也就是i的p可以增加，那么a的下一个字符，一定得是b！也就是说只有这样：babebab，i的p值才能扩张，问题来了，如果后面是b自然扩张成功，但后面可以是b么？？？如果是b，那e的最长回文子串还是abeba么？不是左右都多了一个b？
所以，当mx覆盖了i，但是p[j]超出了id的最长子串的范围时，p[i]就是mx-i！只有这一种可能！
BA|AB…|…BA|A
这就是马拉车对对称的妙用，可以用上面这个图形来解释，三条|从做到右分别表示j,id,i。id的最长回文子串只辐射了 B（A|AB…|…BA|A）部分，而j的最长回文子串辐射了（BA|AB）…|…BA|A，这时候i一定只能辐射BA|AB…|…B（A|A）！因为i和j是关于id对称的啊，只要i想多辐射一点点，哪怕从B里面给了一个字符，id的最长回文子串就变长了…
然而，如果mx-i=p[j]，刚刚好，id刚好覆盖了p[j]，i后面什么情况就不好说了，这个时候才会去试着继续扩张。
总而言之，在mx-i

一直动态记录着最右边的回文子串，加上上面这些大部分情况的简化计算，让整个马拉车算法对每一个位置最多只会访问一个常数级别的次数，因此把时间复杂度控制在了线性。值得一提的是，最坏情况是所有字符都一样的情况，如aaaa这种；

还有边界条件、字符串越界的问题，如java没有\0所以需要在最后补一个字符，其他就不多讲了，慢慢敲，多理解~