Kaggle实战之Titanic: Machine Learning from Disaster

最近埋头苦读，啃机器学习的算法和编程，真是非(xiang)常(dang)欢(lan)乐(sou)呢~ 于是开始自我膨胀跃跃欲试。
嗯，那就从Kaggle的playground开始吧，找了个经典而又浪漫的爱情故事—泰坦尼克，应该能引起我的兴趣好好挖掘吧~

"You jump! I jump! "，『Jack and Rose』的故事想必大家都很熟悉。爱情故事很动人，但是泰坦尼克号在与冰山相撞后沉没后，2224名乘客中有1502人死亡。尽管幸存者有一些运气因素，但是是否获救其实并非随机，而是基于一些背景有rank先后的，比如女人，孩子和上流社会。在这个挑战中，我们需要根据乘客的个人信息和存活情况，运用机器学习工具来预测哪些乘客在悲剧中幸存下来。这是一个典型的二分类问题。
Titanic: Machine Learning from Disaster

1. 首先从整体观察数据情况

• 可用.info()，.describe()查看数据的基本信息和统计特征
  

#-*- coding: utf-8 -*-
import numpy as np
import pandas as pd
from pandas import DataFrame,Series
data_train = pd.read_csv("train.csv")    #读取训练数据
data_train.columns                       #展示数据数据的表头
data_train.info()
data_train.describe()

RangeIndex: 891 entries, 0 to 890
Data columns (total 12 columns):
PassengerId    891 non-null int64
Survived       891 non-null int64
Pclass         891 non-null int64
Name           891 non-null object
Sex            891 non-null object
Age            714 non-null float64
SibSp          891 non-null int64
Parch          891 non-null int64
Ticket         891 non-null object
Fare           891 non-null float64
Cabin          204 non-null object
Embarked       889 non-null object
dtypes: float64(2), int64(5), object(5)
memory usage: 83.6+ KB

	PassengerId	Survived	Pclass	Age	SibSp	Parch	Fare
count	891.000000	891.000000	891.000000	714.000000	891.000000	891.000000	891.000000
mean	446.000000	0.383838	2.308642	29.699118	0.523008	0.381594	32.204208
std	257.353842	0.486592	0.836071	14.526497	1.102743	0.806057	49.693429
min	1.000000	0.000000	1.000000	0.420000	0.000000	0.000000	0.000000
25%	223.500000	0.000000	2.000000	20.125000	0.000000	0.000000	7.910400
50%	446.000000	0.000000	3.000000	28.000000	0.000000	0.000000	14.454200
75%	668.500000	1.000000	3.000000	38.000000	1.000000	0.000000	31.000000
max	891.000000	1.000000	3.000000	80.000000	8.000000	6.000000	512.329200

我们可以看到数据中大概有以下这些字段

PassengerId => 乘客ID
Pclass => 乘客舱级(1/2/3等舱位)
Name => 乘客姓名
Sex => 性别
Age => 年龄
SibSp => 堂兄弟/妹个数
Parch => 父母与小孩个数
Ticket => 船票信息
Fare => 票价
Cabin => 舱位编号
Embarked => 登船港口（3个港口)
Survived => 幸存情况（1为幸存）


其中，我们可以观察到

• 乘客舱级，性别，登船港口，幸存情况，堂兄妹个数、父母与小孩个数是离散属性
• 年龄，票价为连续值属性
• 乘客ID, 乘客姓名，船票信息，舱位编号等属性具有唯一值
• 年龄、舱位编号 有缺失值

2. 数据可视化，分析属性特征

可做数据分析的图标类型有：

• 线型图
• 柱形图
• 直方图
• 散点图
• 密度图
• 箱型图
  
  

其中:

• 离散属性，可用柱状图观察属性每种类别的分布情况
  
• 年龄，票价为连续值属性，可用散点、线性或者密度图来描述分布情况
  
• 堂兄妹个数、父母与小孩个数， 可试验
  
• 乘客ID, 乘客姓名，船票信息，舱位编号等信息，可找源数据观察数据特征，价值有待挖掘
  

首先分析几个离散属性本身的特征情况

#coding:utf-8
import matplotlib.pyplot as plt
plt.rc('figure',figsize=(8,6))
plt.rcParams['font.sans-serif']=['SimHei'] #用来正常显示中文标签
plt.rcParams['axes.unicode_minus']=False #用来正常显示负号
fig = plt.figure()
fig.set(alpha=0.2)  # 设定图表颜色alpha参数

fig.add_subplot(2,2,1)
data_train.Survived.value_counts().plot(kind="bar")
plt.ylabel(u"人数")
plt.title(u"获救情况（1为获救）")

fig.add_subplot(2,2,2)
data_train.Pclass.value_counts().plot(kind="bar")
plt.ylabel(u"人数")
plt.title(u"舱级情况")

fig.add_subplot(2,2,3)
data_train.Sex.value_counts().plot(kind="bar")
plt.ylabel(u"人数")
plt.title(u"性别情况")

fig.add_subplot(2,2,4)
data_train.Embarked.value_counts().plot(kind="bar")
plt.ylabel(u"人数")
plt.title(u"登船港口情况")

Text(0.5,1,'登船港口情况')

由上图可以得到以下信息：

1. 三个舱位人数： 3级 > 1级 > 2级 ，3级的人数基本是其他两个舱级总和。
2. 获救人数大概只有30%
3. 乘客中男性比例大于女性
4. 三个登船港口人数：S > C > G ,其中S 登船港口人数最多

分析离散属性与最终目标值的关系

1.不同乘客等级的获救情况

• 如图可以看出乘客等级的获救概率为： 1 > 2 > 3

Survived0=data_train.Pclass[data_train.Survived==0]
Survived1=data_train.Pclass[data_train.Survived==1]
df=DataFrame({u'不获救':Survived0.value_counts(),u'获救':Survived1.value_counts()})
df.plot(kind='bar',stacked=True)
plt.xlabel(u"乘客等级") 
plt.ylabel(u"人数")
plt.title(u"各乘客等级的获救情况")
plt.show()

2.不同性别的获救情况

• 如图可以看到女性的获救概率比男性的获救概率要高

Survived0=data_train.Sex[data_train.Survived==0]
Survived1=data_train.Sex[data_train.Survived==1]
df=DataFrame({u'不获救':Survived0.value_counts(),u'获救':Survived1.value_counts()})
df.plot(kind='bar',stacked=True)
plt.xlabel(u"性别") 
plt.ylabel(u"人数")
plt.title(u"不同性别的获救情况")
plt.show()

3.不同登船港口的情况

• 可以看出港口的获救情况：C>S>Q

Survived0=data_train.Embarked [data_train.Survived==0]
Survived1=data_train.Embarked [data_train.Survived==1]
df=DataFrame({u'不获救':Survived0.value_counts(),u'获救':Survived1.value_counts()})
df.plot(kind='bar',stacked=True)
plt.xlabel(u"登船港口") 
plt.ylabel(u"人数")
plt.title(u"不同登船港口的获救情况")
plt.show()

分析两个连续值 年龄和票价 本身属性的特征

• 一般用直方图、密度图 （两者反应的信息是相似的）
• 如图可以看出：乘客年龄的分布主要是集中在20-40岁之间，同时，票价集中在0-50之间，由部分土豪消费较高

import pandas as pda
from pandas import DataFrame,Series
# fig,axes=plt.subplots(1,1)
fig=plt.figure()
fig.add_subplot(2,1,1)
# data_train.Age.plot(kind='kde')
data_train.Age.hist()
plt.title(u"年龄分布情况")
fig.add_subplot(2,1,2)
# data_train.Fare.plot(kind='kde')
data_train.Fare.hist()
plt.title(u"票价分布情况")

Text(0.5,1,'票价分布情况')

两个连续值与最终获救情况的关系

• 可根据最终分类将数值分为几组，比较直方图或者密度图的差异
• 可用散点图、箱型图

Survived0=data_train.Age[data_train.Survived==0]
Survived1=data_train.Age[data_train.Survived==1]
df=DataFrame({u'不获救':Survived0,u'获救':Survived1})
df.plot(kind='kde')
plt.xlabel(u"年龄") 
plt.ylabel(u"核密度")
plt.title(u"不同获救情况的年龄分布密度图")
plt.show()

Survived0=data_train.Fare[data_train.Survived==0]
Survived1=data_train.Fare[data_train.Survived==1]
df=DataFrame({u'不获救':Survived0,u'获救':Survived1})
df.plot(kind='kde',xlim=[-50,400])
plt.xlabel(u"票价") 
plt.ylabel(u"核密度")
plt.title(u"不同获救情况的票价分布密度图")
plt.show()

接下来可以分析组合多个属性，得到有价值的信息

首先看看有重要影响的因素——舱级，分别与年龄、票价、港口的关系

Pclass1=data_train.Age[data_train.Pclass==1]
Pclass2=data_train.Age[data_train.Pclass==2]
Pclass3=data_train.Age[data_train.Pclass==3]
df=DataFrame({u'舱级1':Pclass1,u'舱级2':Pclass2,u'舱级3':Pclass3})
df.plot(kind='kde')
plt.xlabel(u"年龄") 
plt.ylabel(u"核密度")
plt.title(u"不同舱级的年龄分布密度图")
plt.show()

Pclass1=data_train.Fare[data_train.Pclass==1]
Pclass2=data_train.Fare[data_train.Pclass==2]
Pclass3=data_train.Fare[data_train.Pclass==3]
df=DataFrame({u'舱级1':Pclass1,u'舱级2':Pclass2,u'舱级3':Pclass3})
df.plot(kind='kde',xlim=[-50,400])
plt.xlabel(u"票价") 
plt.ylabel(u"核密度")
plt.title(u"不同舱级的票价分布密度图")
plt.show()

Pclass1=data_train.Embarked [data_train.Pclass==1]
Pclass2=data_train.Embarked [data_train.Pclass==2]
Pclass3=data_train.Embarked [data_train.Pclass==3]
df=DataFrame({u'舱级1':Pclass1.value_counts(),u'舱级2':Pclass2.value_counts(),u'舱级3':Pclass3.value_counts()})
df.plot(kind='bar',stacked=True)
plt.xlabel(u"港口") 
plt.ylabel(u"核密度")
plt.title(u"不同舱级的港口占比图")
plt.show()

Embarked_C =data_train.Fare[data_train.Embarked =='C']
Embarked_Q =data_train.Fare[data_train.Embarked =='Q']
Embarked_S =data_train.Fare[data_train.Embarked =='S']
df=DataFrame({u'港口C':Embarked_C,u'港口Q':Embarked_Q,u'港口S':Embarked_S})
df.plot(kind='kde',xlim=[-50,400])
plt.xlabel(u"票价") 
plt.ylabel(u"核密度")
plt.title(u"不同港口的票价分布图")
plt.show()

data_train.groupby(['SibSp','Survived']).count()

		PassengerId	Pclass	Name	Sex	Age	Parch	Ticket	Fare	Cabin	Embarked
SibSp	Survived
0	0	398	398	398	398	296	398	398	398	49	398
	1	210	210	210	210	175	210	210	210	77	208
1	0	97	97	97	97	86	97	97	97	17	97
	1	112	112	112	112	97	112	112	112	52	112
2	0	15	15	15	15	14	15	15	15	1	15
	1	13	13	13	13	11	13	13	13	5	13
3	0	12	12	12	12	8	12	12	12	1	12
	1	4	4	4	4	4	4	4	4	2	4
4	0	15	15	15	15	15	15	15	15	0	15
	1	3	3	3	3	3	3	3	3	0	3
5	0	5	5	5	5	5	5	5	5	0	5
8	0	7	7	7	7	0	7	7	7	0	7

Survived0=data_train.SibSp[data_train.Survived==0].value_counts()   # 通过布尔索引
Survived1=data_train.SibSp[data_train.Survived==1].value_counts()
Survived1=Series(Survived1,index=Survived0.index)
Survived1=Survived1.fillna(0)
num=Survived0+Survived1
Survived_rate=Survived1/num
Survived_rate=Survived_rate.sort_index()
plt.figure()
Survived_rate.plot()
plt.xlabel(u"兄弟/妹个数") 
plt.ylabel(u"存活率(%)")
plt.title(u"兄弟/妹个数对幸存率的影响")
plt.show()

data_train.groupby(['SibSp','Survived']).count()

		PassengerId	Pclass	Name	Sex	Age	Parch	Ticket	Fare	Cabin	Embarked
SibSp	Survived
0	0	398	398	398	398	296	398	398	398	49	398
	1	210	210	210	210	175	210	210	210	77	208
1	0	97	97	97	97	86	97	97	97	17	97
	1	112	112	112	112	97	112	112	112	52	112
2	0	15	15	15	15	14	15	15	15	1	15
	1	13	13	13	13	11	13	13	13	5	13
3	0	12	12	12	12	8	12	12	12	1	12
	1	4	4	4	4	4	4	4	4	2	4
4	0	15	15	15	15	15	15	15	15	0	15
	1	3	3	3	3	3	3	3	3	0	3
5	0	5	5	5	5	5	5	5	5	0	5
8	0	7	7	7	7	0	7	7	7	0	7

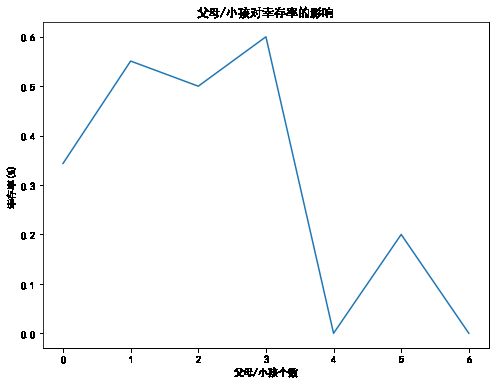
Survived0=data_train.Parch[data_train.Survived==0].value_counts()
Survived1=data_train.Parch[data_train.Survived==1].value_counts()
Survived1=Series(Survived1,index=Survived0.index)
Survived1=Survived1.fillna(0)
num=Survived0+Survived1
Survived_rate=Survived1/num
Survived_rate=Survived_rate.sort_index()
plt.figure()
Survived_rate.plot()
plt.xlabel(u"父母/小孩个数") 
plt.ylabel(u"幸存率(%)")
plt.title(u"父母/小孩对幸存率的影响")
plt.show()

Survived_noCabin=data_train.Survived[data_train.Cabin.isnull()]
Survived_haveCabin=data_train.Survived[data_train.Cabin.notnull()]
df=DataFrame({'无':Survived_noCabin.value_counts(),'有':Survived_haveCabin.value_counts()}).transpose()
df.plot(kind='bar', stacked=True)
plt.title(u"按Cabin有无看获救情况")
plt.xlabel(u"Cabin有无") 
plt.ylabel(u"人数")
plt.show()

3.缺失值处理

通常遇到缺值的情况，我们会有几种常见的处理方式

1. 如果缺值的样比例极高，直接舍弃，因为作为特征可能反倒带入noise，影响结果
   
2. 如果缺值的样本适中，而该属性是离散值(比如说类目属性)，那就把NaN作为一个新类别，加到类别特征中
   
3. 如果缺值的样本适中，而该属性为连续值，有时候我们会考虑给定一个step(比如这里的age，我们可以考虑每隔2/3岁为一个步长)，然后把它离散化，之后把NaN作为一个type加到属性类目中。
   
4. 有些情况下，缺失的值个数并不是特别多，那我们也可以试着根据已有的值，使用模型拟合一下数据，补充上。
   

在第1步的源数据分析中，我们知道Age 和Cabin 有缺失值

其中 :

• Cabin 字段缺失太多，暂时按Cabin有无数据，将这个属性处理成Yes和No两种类
  
• Age 字段 通过模型拟合，补充数据

# Cabin 的缺失值填充函数
def set_Cabin_type(df):
#     df.Cabin[df.Cabin.notnull()]='YES'
#     df.Cabin[df.Cabin.isnull()]='NO'
    df.loc[(df.Cabin.notnull()),'Cabin']='YES'
    df.loc[(df.Cabin.isnull()),'Cabin']='NO'
    return df
data_train=set_Cabin_type(data_train)

# 使用 RandomForestClassifier 填补缺失的年龄属性
from sklearn.ensemble import RandomForestRegressor
def set_missing_ages(df):
    # 把已有的数值型特征取出来丢进Random Forest Regressor中,因为逻辑回归算法输入都需要数值型特征
    age_df = df[['Age','Fare', 'Parch', 'SibSp', 'Pclass']]
    age_known=age_df.loc[age_df.Age.notnull()].values   # 要用sklearn的模型，输入参数要把Series和DataFrame 转成nparray 
    age_unknown=age_df.loc[age_df.Age.isnull()].values
    #将有值的年龄样本 训练数据，然后用训练好的模型用于 预测 缺失的年龄样本的值
    #训练数据的特征集合
    X=age_known[:,1:]
    #训练数据的目标
    y=age_known[:,0]
    
    #构建随机森林回归模型器
    rfr = RandomForestRegressor(random_state=0, n_estimators=2000, n_jobs=-1)
    # 拟合数据,训练模型
    rfr.fit(X,y)
    # 用训练好的模型 预测 有缺失值的年龄属性
    predictedAges=rfr.predict(age_unknown[:,1:])
    # 得到的预测结果，去填补缺失数据
    df.loc[df.Age.isnull(),'Age']=predictedAges
    return df,rfr

data_train,rfr=set_missing_ages(data_train)    
    

4.类目型特征因子化

因为逻辑回归建模时，需要输入的特征都是数值型特征，我们通常会先对类目型的特征进行转化

• 当类目型特征值 与数值大小有关联关系时，比如大小S,M,L，可以映射为数值型，比如分别映射为 1，2，3。
  
• 当类目型特征值 仅仅表示类别，没有大小关系，则需要使用 因子化/one-hot编码，使用pandas的.get_dummies函数。
  

类目型特征有：Cabin、Embarked、Sex、Pclass

dummies_Cabin = pd.get_dummies(data_train.Cabin,prefix='Cabin') #ptefix 是前缀，因子花之后的字段名为 前缀_类名

dummies_Embarked = pd.get_dummies(data_train['Embarked'], prefix= 'Embarked')

dummies_Sex = pd.get_dummies(data_train['Sex'], prefix= 'Sex')

dummies_Pclass = pd.get_dummies(data_train['Pclass'], prefix= 'Pclass')

df = pd.concat([data_train, dummies_Cabin, dummies_Embarked, dummies_Sex, dummies_Pclass], axis=1) #将哑编码的内容拼接到data_train后
df.drop(['Pclass', 'Name', 'Sex', 'Ticket', 'Cabin', 'Embarked'], axis=1, inplace=True)  # 把编码前的字段删除

5.标准化和归一化

对于量纲差异太大的数值型特征，我们需要将其标准化或归一化到一个范围，不然会对建模产生很大的影响（比如逻辑回归和梯度下降）

• 其中有 preprocessing 中的MinMaxScaler类、MinMaxScaler类、Normalizer类等

需要做 scaleing的 特征有： Age、Fare

# 这里用StandardScaler类对
from sklearn.preprocessing import StandardScaler
# 创建一个定标器
scaler=StandardScaler()
# 拟合数据 
#---fit和transform为两个动作，可用fit_transform 合并完成
#df['Age_Scale']=scaler.fit_transform(df.Age.values.reshape(-1,1))  # 若为单个特征，需要reshape为（-1,1）

#--但是由于test和train 需要用同一个fit出来的参数，所以需要记录fit参数，用于test数据的标准化，因此分开计算
Age_Scale_parame=scaler.fit(df.Age.values.reshape(-1,1))
#df['Age_Scale']=scaler.transform(df.Age.values.reshape(-1,1))
df['Age_Scale']=scaler.fit_transform(df.Age.values.reshape(-1,1),Age_Scale_parame)

Fare_Scale_parame=scaler.fit(df.Fare.values.reshape(-1,1))
df['Fare_Scale']=scaler.fit_transform(df.Age.values.reshape(-1,1),Fare_Scale_parame)
df.drop(['Age', 'Fare'], axis=1, inplace=True)

到这里，我们的数据预处理就结束了。

6.训练模型

接下来，我们用逻辑回归算法将训练数据进行训练模型

from sklearn.linear_model import LogisticRegression
df_train=df.filter(regex='Survived|Age_.*|SibSp|Parch|Fare_.*|Cabin_.*|Embarked_.*|Sex_.*|Pclass_.*').values #用正则表达式把需要的字段过滤出来
# 训练特征
df_train_feature=df_train[:,1:]
#训练目标
df_train_label=df_train[:,0]
#构建逻辑回归分类器
clf=LogisticRegression(C=1.0, penalty='l1', tol=1e-6)
#拟合数据
clf.fit(df_train_feature,df_train_label)
clf

LogisticRegression(C=1.0, class_weight=None, dual=False, fit_intercept=True,
          intercept_scaling=1, max_iter=100, multi_class='ovr', n_jobs=1,
          penalty='l1', random_state=None, solver='liblinear', tol=1e-06,
          verbose=0, warm_start=False)

7.测试模型

我们对测试数据 做训练数据相同的数据预处理，包括：

• 缺失值填充：Age,Cabin,Fare
  
• 类目特征因子化： Pclass、Sex、Cabin、Embarked
  
• 归一化 ： Age、Fare

data_test = pd.read_csv("test.csv")
# 缺失值填充
data_test.loc[data_test.Fare.isnull(),'Fare']=0
data_test= set_Cabin_type(data_test)
age_data = data_test[['Age','Fare', 'Parch', 'SibSp', 'Pclass']]
age_test=age_data[age_data.Age.isnull()].values
# age的缺失值填充也用前训练数据 的age值fit计算的模型,所以可以直接预测
predictedAges = rfr.predict(age_test[:,1:])
data_test.loc[data_test.Age.isnull(),'Age'] = predictedAges

# 类目特征因子化
dummies_Cabin = pd.get_dummies(data_test.Cabin, prefix= 'Cabin')
dummies_Sex = pd.get_dummies(data_test.Sex, prefix= 'Sex')
dummies_Pclass = pd.get_dummies(data_test.Pclass, prefix= 'Pclass')
dummies_Embarked = pd.get_dummies(data_test.Embarked, prefix= 'Embarked')

#归一化也用训练数据fit出来的参数进行转化
data_test['Age_scaled'] = scaler.fit_transform(data_test['Age'].values.reshape(-1, 1), Age_Scale_parame)
data_test['Fare_scaled'] = scaler.fit_transform(data_test['Fare'].values.reshape(-1, 1), Fare_Scale_parame)

# 拼接处理后数据以及删除处理前数据
df_test = pd.concat([data_test, dummies_Cabin, dummies_Embarked, dummies_Sex, dummies_Pclass], axis=1)
df_test.drop(['Pclass', 'Name', 'Sex', 'Ticket', 'Cabin', 'Embarked','Age','Fare'], axis=1, inplace=True)

将测试数据 用训练数据训练出来的模型 进行预测

df_test=df_test.values
# df_test = df_test.filter(regex='Age_.*|SibSp|Parch|Fare_.*|Cabin_.*|Embarked_.*|Sex_.*|Pclass_.*')  #可用正则表达式取删选数据
predict_result=clf.predict(df_test[:,1:])
result = pd.DataFrame({'PassengerId':data_test['PassengerId'].values, 'Survived':predict_result.astype(np.int32)})
result.to_csv("logistic_regression_predictions.csv", index=False)

pd.read_csv("logistic_regression_predictions.csv")

	PassengerId	Survived
0	892	1
1	893	0
2	894	1
3	895	0
4	896	0
5	897	0
6	898	1
7	899	0
8	900	0
9	901	0
10	902	0
11	903	0
12	904	0
13	905	0
14	906	0
15	907	0
16	908	1
17	909	0
18	910	0
19	911	0
20	912	0
21	913	0
22	914	0
23	915	0
24	916	1
25	917	0
26	918	0
27	919	0
28	920	0
29	921	0
...	...	...
388	1280	1
389	1281	0
390	1282	0
391	1283	0
392	1284	0
393	1285	0
394	1286	0
395	1287	0
396	1288	1
397	1289	0
398	1290	0
399	1291	1
400	1292	1
401	1293	0
402	1294	0
403	1295	0
404	1296	0
405	1297	0
406	1298	0
407	1299	1
408	1300	1
409	1301	0
410	1302	1
411	1303	1
412	1304	0
413	1305	0
414	1306	0
415	1307	0
416	1308	0
417	1309	0

418 rows × 2 columns

把预测结果提交到Kaggle官网，得到准确率为：0.76555。

没错，效果还不够理想，因为简单分析过后出的一个baseline系统，前面数据探索出来的结论还没用上呢，真正的挖掘工作现在才刚刚开始呢~~~

接下来将对模型状态进行分析，并做一系列的优化工作。

未完待续...

---

本文参考了来自寒小阳的github:Kaggle_Titanic，有兴趣的小伙伴可以看看。

转载于:https://www.cnblogs.com/laiyaling/p/10077454.html