the Art of Network-flows(网络流24题小结 chapter I)
文章目录
- 飞行员配对方案问题
- 试题库问题
- 方格取数问题
- 最小路径覆盖问题
- 魔术球问题
- 最长不下降子序列问题
飞行员配对方案问题
原题链接:洛谷P2756
——题意——
现在有 n ( < 100 ) n(<100) n(<100)名飞行员,其中 1 1 1到 m m m为外籍飞行员和 m + 1 m+1 m+1到 n n n为英国飞行员,已知外籍飞行员 i i i和英国飞行员 j j j可以配合(一名外籍飞行员可能与多位英国飞行员可以配合),现在需要对外籍飞行员和英国飞行员一一配对,求出最多的匹配队数,并给出匹配方案。
——题解——
这是一道裸的二分图求最大匹配问题,也是网络流24题中最简单的。把飞行员分成外籍和英国籍两部分,每个飞行员看成一个点,对于可以匹配的飞行员之间,由外籍飞行员向英国飞行员连一条容量为 1 1 1的边。建立一个源点,向各个外籍飞行员连一条容量为 1 1 1的边;建立一个汇点,各个英国飞行员向其连一条容量为 1 1 1的边。对于样例,我们建立如下图所示的二分图:
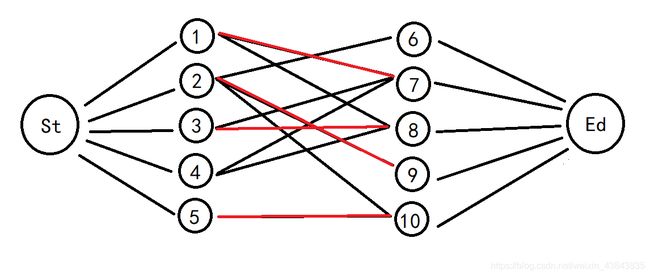
(图中,所有边流量都为1,从左指向右,红线为匹配方案)
——Code——
#include 试题库问题
原题链接:洛谷P2763
——题意——
现在有 ( 2 < = ) k ( < = 20 ) (2<=)k(<=20) (2<=)k(<=20)种题型和 ( k < = ) n ( < = 1000 ) (k<=)n(<=1000) (k<=)n(<=1000)道题目,总共需要抽取 m m m个题目组成一份试卷,其中对于每一种题型都有固定的需求个数,每道题目可能属于几种题型。现在要求找到一种组成试卷的方案。
——题解——
这道题很好建模,把题目看做点集一,题型看做点集二。若某道题从属于某题型,则从题目向题型连一条容量为 1 1 1的有向边。从源点向各个题目连接一条容量为 1 1 1的边,各个题型向汇点连一条容量等同于需求量的边。一条从源点指向汇点的流表示,选取某题目,求把该题归为某题型。如果最后流向汇点的边都满流,则存在可行方案。
——Code——
#include
// }
for(int i=1;i<=n;++i){
if(match[i]){
showAns[match[i]-n].push_back(i);
}
}
for(int i=1;i<=k;++i){
printf("%d:",i);
for(unsigned int j=0;j<showAns[i].size();++j){
printf(" %d",showAns[i][j]);
}
printf("\n");
}
}
return 0;
}
方格取数问题
原题链接:洛谷P2774
——题意——
给出一个 m ( < = 100 ) m(<=100) m(<=100)行 n ( < = 100 ) n(<=100) n(<=100)列的棋盘,每个格子上都有一个权值为正的棋子,你需要取走其中任意数量的棋子,取走的棋子之间不能有公共边,求出取出棋子的最大权值和。
——题解——
在建模之前,需要弄明白一些细节。所有棋子的权值总和是一定的,取走棋子的过程,可以看做舍弃其它棋子的过程。取走棋子之间没有公共边,即相邻的棋子最多去掉其中一个,我们当然是希望去掉权值小的那一枚。如此,不妨先把棋盘中的棋子拆成互相没有公共边的两个点集,用一个源点连向点集一中的各个点,各边容量为棋子权值;在用一个汇点,使点集二中的点指向它,容量为棋子权值。对于两个点集,如果棋子之间相邻,则对应的点之间连一条流量 I N F INF INF的边,由点集一连向点集二。这样以来,一条从原点往汇点的流,表示删除两个相邻棋子之间权值较小的棋子。于是,发挥网络流模型可以不断调整的优势,走一遍二分图最大流,即可得出去掉棋子权值和的最小值。以样例为例,建图如下:
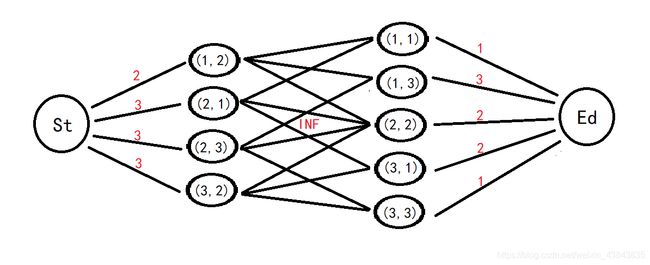
(图中,所有边从左指向右)
——Code——
#include 最小路径覆盖问题
原题链接:洛谷P2764
——题意——
给出一个有向无环图,其中结点数为 n ( < = 150 ) n(<=150) n(<=150),边数为 m ( < = 6000 ) m(<=6000) m(<=6000),要求用最少的路径,使图中所有的点都恰好被经过一次。输出每一条路径各自经过的结点。
——题解——
在学网络流之前,很容易想到这题需要用一种贪心策略来解决,即先找出一条最长的路径,然后再找次长路径,直到图中只剩下一些孤立点。但是,当我们用直接贪心找到一条最长路径时,这条路径上包含哪些点是确定的,或者说存在多条长度相同但是包含结点不同的路径,那么这个时候,怎么保证直接贪心得出的路径就一定包含在最优解之中呢?网络流模型有一个好处,即使当前找到一条路径,在后续增加流量时,依旧能在不改变路径长度的情况下更改这条路径具体包含的结点。本题用网络流模型,可以充分利用到其自动调整的优势。首先处理“每个点只能被经过一次”,把一个结点 i i i拆成两个,分别记为 a i ai ai和 b i bi bi,同理,把结点集拆成两个集合,分别为A和B。如果点 i i i和点 j j j之间存在有向边,则由 a i ai ai向 b j bj bj连一条容量为 1 1 1的有向边。源点向所有的 a i ai ai连一条容量为 1 1 1的边,所有的 b i bi bi向汇点连一条容量为 1 1 1的边。从源点到汇点的流表示,结点 i i i连向结点 j j j的边包含在某条路径中。如此一来,输出路径只需要迭代输出每个结点的匹配结点,孤立点输出其自身。以样例为例建图:
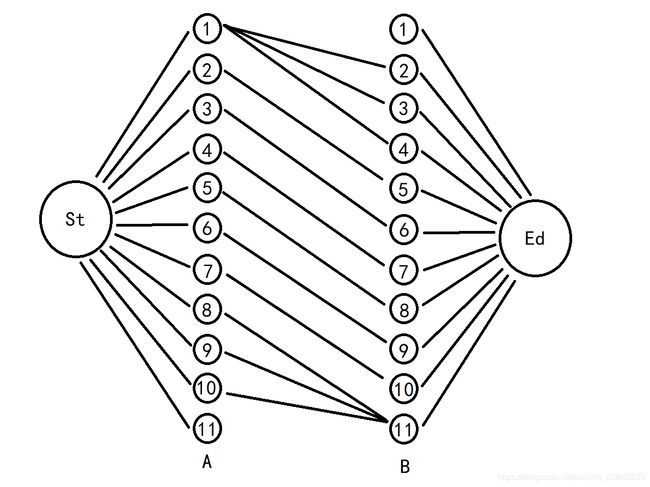
(图中,每条边都从左指向右,且容量为1)
——Code——
#include 魔术球问题
——题意——
现在给你 n ( < = 55 ) n(<=55) n(<=55)根柱子,把数字对应的小球叠着放在柱子上。小球之间叠加的规则是:相邻两个小球编号之和为一个平方数。小球的编号从 1 1 1开始,现在需要求出这 n n n根柱子最多能承载多少小球。‘
——题解——
’本题是上面最小路径覆盖问题的一个变式。可以反向思考,对于一个特定数量的小球,最少需要多少根柱子。因此和上题一样,把一个小球拆成两个点,能构成平方数的小球,则从编号小的连向编号大的。每次新加入一个小球计算最小需要的柱子数,如果柱子数大于 n n n,则当前小球编号减 1 1 1即为 n n n根柱子承载的最大数量。利用网络流的优势,新加入的球在之前的残余网络上进行增广,所以复杂度并不会很高。
——Code——
#include 最长不下降子序列问题
原题链接:洛谷P2766
——题意——
给出一个长度为 n ( < = 500 ) n(<=500) n(<=500)的序列, x 1... x n x1...xn x1...xn,求解三个问题:
1)最长不下降子序列的长度;
2)原序列中最多可以取多少个这样的最长子序列;
3)如果 x 1 x1 x1和 x n xn xn可以重复利用,最多有多少个最长子序列。
——题解——
第一小问可以用动态规划解决 ( d p ) (dp) (dp),得出最大长度 l e n len len,顺便得出以每个点为结尾的序列的最长子序列长度(相当于一个拓扑序)。
第二小问,利用上面得出的序列,建立一张拓扑排序图(如果 i > j 且 d p [ i ] = = d p [ j ] + 1 且 x [ i ] > = x [ j ] i>j且dp[i]==dp[j]+1且x[i]>=x[j] i>j且dp[i]==dp[j]+1且x[i]>=x[j], j j j向 i i i连一条容量为 1 1 1的有向边),源点向 d p = 1 dp=1 dp=1的点连一条容量为 1 1 1的有向边, d p = l e n dp=len dp=len的点向汇点连接一条容量为 1 1 1的有向边。为了保证每个点只被使用一次,把每个点拆成两份, a i ai ai向 b i bi bi连一条容量为 1 1 1的有向边,若满足拓扑序,则由 b j bj bj连向 a i ai ai
第三小问,再上图的基础上,把 x 1 x1 x1的两个拆分的之间以及与源点的边容量改成INF, x n xn xn同理。注意 n = 1 n=1 n=1时,需要特判,参见代码。
以序列 1 、 5 、 8 、 2 、 6 1、5、8、2、6 1、5、8、2、6为例建图:
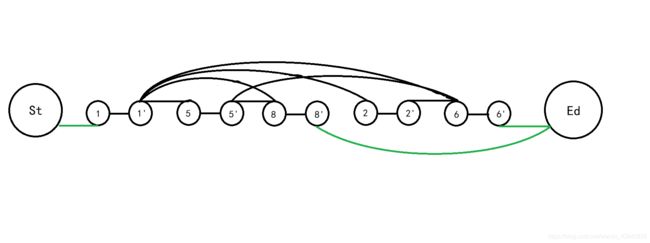
(图中所有边从左指向右)
——Code——
#include