SIEMIWP系列二:二分,排序

SIEMIWP:Sorry I enjoyed myself in water playing:对不起，我在水里玩得很开心

二分

整数二分的两种写法

1. $r=mid,l=mid+1,mid=(l+r)>>1$
2. $l=mid,r=mid-1,mid=(r+l+1)>>1$

不同问题二分写法略有不同,不可混淆!

一般二分

• 特征:

1. 问题可转化为单调函数(定义域:可行方案;值域:方案对应的解)

• 时间复杂度:O(logn)

举例:lowerbound,upperbound函数

二分答案转化为判定

• 特征:

1. 问题可转化为01函数(函数在(-inf,x]=1,[x+1,inf)=0)
2. 题目中有特征为:最大值最小

• 时间复杂度:O(logn)

最佳牛围栏

问题就是在原序列中选取一个长度不小于k的序列使得这个子序列的平均值最大

我们发现,如果二分答案也就是平均值的话,问题就转化为了求01函数的转折点:

于是考虑如何判定平均值是否合法:

若二分的值x合法,也就是不存在一个合法的序列使得其平均值大于x

这个时候就应该识别出O(n)判断是否存在序列平均值大于n的对应方法:

将序列的每个数都减去n,然后O(n)找到最大子段和(又是一个新解题思路),如果和大于0,就存在,反之不存在

于是本题就可以O(nlogn)解决了

import math

xx=input().split()
n=int(xx[0])
f=int(xx[1])

a=[]
s=[]

def Min(a,b):
    if(a>b):
        return b
    else:
        return a

def Max(a,b):
    if(a<b):
        return b
    else:
        return a

def check(mid):
    for i in range(1,n+1,1):
        s[i]=a[i]-mid
        s[i]=s[i-1]+s[i]
    ans= -1e8
    min_val=1e8
    for i in range(1,f,n+1):
        min_val=Min(min_val,s[i-f])
        ans=Max(ans,s[i]-min_val)
    if ans<=0:
        return 0
    else:
        return 1


a.append(0)
s.append(0)
for i in range(1,n+1,1):
    tt=float(input())
    a.append(float(tt))
    s.append(float(0))
l=-1e6
r=1e6
eps=1e-5
while(r-l>eps):
    mid=(l+r)/2
    if(check(mid)):
        l=mid
    else:
        r=mid

print(int(r*1000))

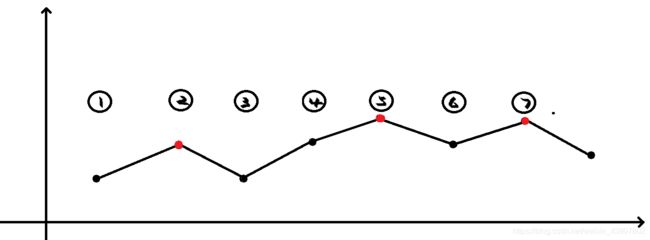
特殊排序

考虑二分位置(答案)

二分方式略微奇葩:
对第k个数:

l=1
r=k
while(l<r):
	mid=(l+r)//2
	if compare(res[mid],k):
		r=mid
	else:
		l=mid+1

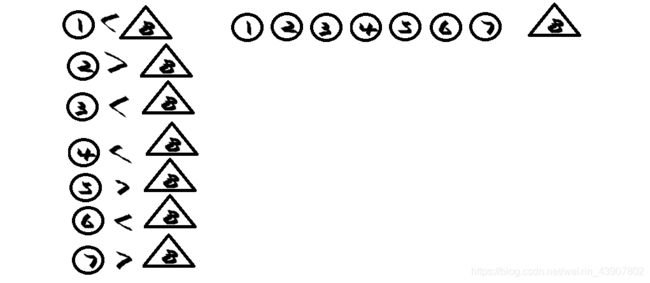
原理:

k-1=7
k=8
大小关系如下:
定义:ii到i+1为上升斜线,反之下降,则:

于是问题就转化为了找到图中的"峰顶"(红点)(i是峰顶 等价于 i>k,i-1

显然我们的二分策略可以在log级别的时间内找到这些点中的一个

class Solution {
public:
    vector<int> specialSort(int N) {
        vector<int> res;
        res.push_back(1);
        for(int i = 2;i <= N;i++){
            int l = 0,r = res.size() - 1;
            while(l <= r){
                int mid = l + r >> 1;
                if(compare(res[mid],i)) l = mid + 1;
                else    r = mid - 1;
            }
            res.push_back(i);
            for(int j = res.size() - 2;j > r;j--)   swap(res[j],res[j + 1]);
        }
        return res;
    }
};

三分

• 特征:严格单峰函数求极值
• 解法:三分(l,midl,midr,r)
• 时间复杂度:log(r-l)