数据结构和算法Java版本(1)简介和稀疏数组
数据结构和算法Java版本(1)简介
1.经典算法面试题:
字符串匹配问题:
有一个字符串 str:“山东宏伟收获的哦豁的哦好的哦好的”,和一个子串 str2=“哦好的哦好的”,现在要判断str1是否含有str2,如果存在,就返回第一次出现的位置,如果没有,则返回-1,要求用最快速度完成匹配,你的思路是什么?
暴力匹配(简单、效率低)
KMP算法《部分匹配表》
汉罗塔小游戏
请完成汉罗塔游戏的代码,要求:
1)将A的所有圆盘移动到C,并且规定2)小圆盘上不能放大圆盘3)三根柱子之间只能移动一个圆盘
八皇后问题
回溯算法的典型案例,该问题是国际西洋棋手马克思~贝瑟尔与1848年提出:在8*8的国际象棋上摆八个皇后,使其不能够互相攻击即:任意两个皇后都不能处于同一行同一列或同一斜线上,问有多少种不同摆法,【92】=》分治算法
马踏棋盘算法
1)马踏棋盘算法被称为骑士周游问题
2)将马随机放在国际象棋的8*8棋盘,Board**{07}{07}**的某个方格中,马按走棋规则(马走日)进行移动,要求每个方格只进入一次,走遍棋盘上全部64个方格
3)图的深度优化算法(DFS)+贪心算法优化
数据结构和算法内容重要性
1)算法是程序的灵魂(十大常用算法)
2)一般来说程序会使用了内存计算框架(如spark)和缓存技术(比如Redis)来优化程序,再深入的思考有关这些计算框架和缓存技术,它的核心部分
3)Unix下开发服务器程序,功能是要支持千万人同时在线,所以对代码优化尤为重要
4)程序员面试门槛越来越高
5)如果不想永远拧螺丝就花下时间来造轮子,研究数据结构和算法
6)目标掌握本质,在工作中灵活运用解决实际问题和优化题目
数据结构和算法介绍
1.数据结构是研究组织数据方式的学科,有编程语言就有了数据结构,学好数据结构就可以编写出更漂亮有效率的demo
2.程序=数据结构+算法
3.数据结构是算法的基础,想学好算法,需要把数据结构学到位
问题一:字符替换问题
Java代码:
public static void main(String[] args){
String str="Java,Java,Java,Java,hello,world!";
String newStr=str.replaceAll("Java","mwq~");//算法
System.out.println("newStr="+ newStr);
}
写出用单链表表示的字符串类,及字符串结点类的定义,并依次实现它的构造函数、以及计算串长度,串赋值,判断两串相等、求子串、两串连接、求子串在串中位置等7个成员函数。
线性结构和非线性结构
数据结构包括线性结构和非线性结构。
线性结构:
1)最常用的数据结构,特点是数据元素之间存在一对一的线性关系
2)线性结构有两种不同的存储结构,即顺序存储结构和链式存储元素。顺序存储的线性表称为顺序表,顺序表中的存储元素是连续的,地址连续。
3)链式存储顺序的线性表称为链表,链表中的存储元素不一定是连续的,元素节点中存放数据元素以及相邻元素的地址信息,链表可以充分利用碎片内存。
4)线性结构常见的有:数组、队列、链表和栈。
非线性结构:
非线性结构包括:二维数组,多维数组,广义表,树结构,图结构
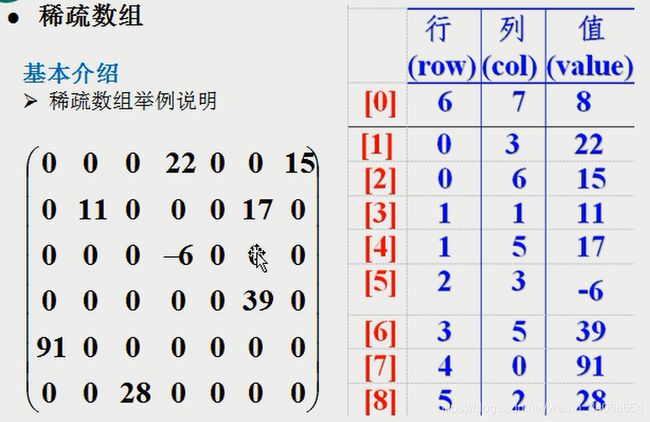
稀疏数组
当一个数组大部分元素为0时,或者值为同一个值得数组时,可以使用细稀疏数组来保存该数组
处理方法:
1)记录数组一共有几行几列,有多个不同的值
2)把具有不同值的元素的行列记录在一个小规模的数组中,从而缩小程序规模
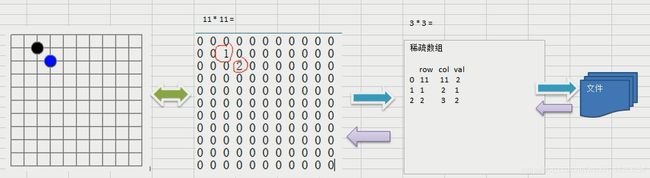
例如五子棋上存储点,无意义的点比较多,引出稀疏数组。
左边实际数组,右边稀疏数组
二维数组转稀疏数组
1.遍历原始的二维数组 ,得到有效数据的个数sum
2.根据sum就可以创建稀疏数组
sparseArr int[sum+1][3]
3.将二维数组的有效数据存入到稀疏数组
稀疏数组转原始的二维数组思路
1.先读取稀疏数组的第一行,根据第一行给出原始的二维数组如
chessArr2=int[11][11]
2.在读取稀疏数组后几行的数据,并赋值给原始的二维数组即可
代码实现:
package com.atguigu.sparsearray;
public class SparseArrary {
public static void main(String[] args) {
//创建一个原始的二维数组11*11
//0:表示没有棋子,1表示黑子,2表示蓝子
int chessArr1[][]=new int [11][11];
chessArr1[1][2]=1;
chessArr1[2][3]=2;
chessArr1[4][5]=2;
//输出原始的二维数组
System.out.println("原始的二维数组");
for(int [] row:chessArr1) {
for(int data:row) {
System.out.printf("%d\t",data);
}
System.out.println();
}
//将二维数组转稀疏数组的思想
//1.先遍历二维数组,得到非0数据的个数
int sum=0;
for(int i=0; i<11;i++) {
for(int j=0;j<11;j++) {
if(chessArr1[i][j]!=0) {
sum++;
}
}
}
//2.创建一个对应的稀疏数组
int sparseArr[][]=new int [sum+1][3];
//给稀疏数组赋值
sparseArr[0][0]=11;
sparseArr[0][1]=11;
sparseArr[0][2]=sum;
//遍历二维数组,将非0的值存放到sparseArr中
int count=0;//用于记录是第几个非0数据
for(int i=0; i<11;i++) {
for(int j=0;j<11;j++) {
if(chessArr1[i][j]!=0) {
count++;
sparseArr[ count][0]=i;
sparseArr[ count][1]=j;
sparseArr[ count][2]=chessArr1[i][j];
}
}
}
//输出稀疏数组的形式
System.out.println();
System.out.println("得到的稀疏数组为如下形式:");
for (int i=0;i<sparseArr.length;i++) {
System.out.printf("%d\t%d\t%d\t\n",sparseArr[i][0],sparseArr[i][1],sparseArr[i][2]);
}
System.out.println();
//将稀疏数组恢复成原始的二维数组
/*
* 1.先读取稀疏数组的第一行,根据第一行给出原始的二维数组如chessArr2=int[11][11]
* 2.在读取稀疏数组后几行的数据,并赋值给原始的二维数组即可
*/
//1.先读取稀疏数组的第一行,根据第一行给出原始的二维数组
int chessArr2[] []=new int[sparseArr[0][0]][sparseArr[0][1]];
//2.在读取稀疏数组后几行的数据(第二行开始),并赋值给原始的二维数组
for (int i=1;i<sparseArr.length;i++) {
chessArr2[sparseArr[i][0]][sparseArr[i][1]]=sparseArr[i][2];
}
//输出恢复后的二维数组
System.out.println();
System.out.println("恢复后的二维数组");
for(int[] row:chessArr2) {
for (int data:row) {
System.out.printf("%d\t",data);
}
System.out.println();
}
}
}
输出结果
原始的二维数组
0 0 0 0 0 0 0 0 0 0 0
0 0 1 0 0 0 0 0 0 0 0
0 0 0 2 0 0 0 0 0 0 0
0 0 0 0 0 0 0 0 0 0 0
0 0 0 0 0 2 0 0 0 0 0
0 0 0 0 0 0 0 0 0 0 0
0 0 0 0 0 0 0 0 0 0 0
0 0 0 0 0 0 0 0 0 0 0
0 0 0 0 0 0 0 0 0 0 0
0 0 0 0 0 0 0 0 0 0 0
0 0 0 0 0 0 0 0 0 0 0
得到的稀疏数组为如下形式:
11 11 3
1 2 1
2 3 2
4 5 2
恢复后的二维数组
0 0 0 0 0 0 0 0 0 0 0
0 0 1 0 0 0 0 0 0 0 0
0 0 0 2 0 0 0 0 0 0 0
0 0 0 0 0 0 0 0 0 0 0
0 0 0 0 0 2 0 0 0 0 0
0 0 0 0 0 0 0 0 0 0 0
0 0 0 0 0 0 0 0 0 0 0
0 0 0 0 0 0 0 0 0 0 0
0 0 0 0 0 0 0 0 0 0 0
0 0 0 0 0 0 0 0 0 0 0
0 0 0 0 0 0 0 0 0 0 0
队列
介绍:
1)队列是一个有序列表,可以用数组或是链表实现
2)遵循先入先出原则,即:先存入队列的数据,要先取出,后存入的要后取出