一篇文章带你快速入门DP动态规划——C++
前言:
博主是一名大一编程小白,因为马上要参加蓝桥杯,所以最近一直在学习动态规划,接下来我将分享我遇到的经典例题和我能力所及的最清晰的代码,并且会逐渐丰富文章内容,分享思路,希望和大家共同进步!
因为内容较多,建议收藏慢慢研究。
学习笔记:
动态规划题目特点
1.计数
—有多少种方式走到右下角
—有多少种方法选出k个数使得和为sum
2.求最大最小值
—从左上角走到右下角路径的最大数字和
—最长上升子序列长度
3.求存在性
—取石子游戏,先手是否必胜
—能不能选出k个数使得和为sum
动态规划组成部分一:确定状态
最后一步(最优策略的最后一步)
化成子问题
动态规划组成部分二:转移方程
动态规划组成部分三:初始条件和边界情况
用转移方程算不出来,需要手工定义
动态规划组成部分四:计算顺序
利用之前的计算结果
一维从小到大(大部分)
二维从上到下,从左到右(大部分)常见动态规划类型
坐标型动态规划
序列型动态规划
划分型动态规划
区间型动态规划
背包型动态规划
最长序列型动态规划
博弈型动态规划
综合性动态规划
例一 Unique Paths
题目描述:
给定m行n列的网格,有一个机器人从左上角(0,0)出发,每一步可以向下或者向右走一步,问有多少种不同的方式走到右下角?
代码如下:
#include
using namespace std;
void dp(int m,int n)
{
int f[m][n];
memset(f,0,sizeof(f));
int i,j;
f[0][0]=1;
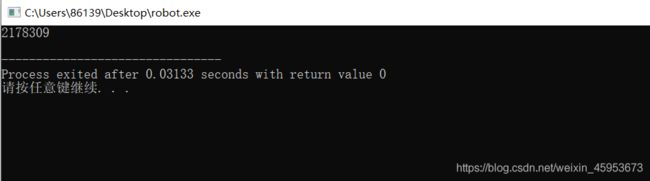
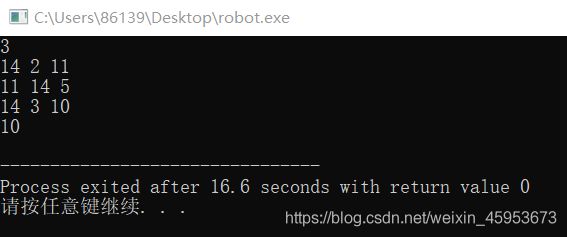
for(j=0;j 运行结果:
例二 激光样式
题目描述:
x星球的盛大节日为增加气氛,用30台激光器一字排开,向太空中打出光柱。
安装调试的时候才发现,不知什么原因,相邻的两台激光器不能同时打开!
国王很想知道,在目前这种bug存在的情况下,一共能打出多少种激光效果?
显然,如果只有3台机器,一共可以成5种样式,即:
全都关上(sorry, 此时无声胜有声,这也算一种)
开一台,共3种
开两台,只1种
30台就不好算了,国王只好请你帮忙了。
要求提交一个整数,表示30台激光器能形成的样式种数。
注意,只提交一个整数,不要填写任何多余的内容。
网上摘抄代码如下:
#include
#include
#include
#include
/* run this program using the console pauser or add your own getch, system("pause") or input loop */
using namespace std;
bool get(int x){
if(x&(x<<1))return false;
else return true;
}
int main(int argc, char *argv[]) {
int ans=0;
for(int i=0;i<1<<30;i++){
if(get(i)){
ans++;
}
}
cout< 网上摘抄代码运行结果:
我的思路:
我的代码如下:
#include
using namespace std;
int main()
{
int arr[31];
int i;
arr[1]=2;
arr[2]=3;
for(i=3;i<=30;i++)
arr[i]=arr[i-1]+arr[i-2];
printf("%d\n",arr[30]);
} 我的代码运行结果:
疑问:
我直接找到了转移方程和出口,此代码非常简单,有点小学生找规律的味道,不知道如果在蓝桥杯这样写对不对。请大佬指正,感谢!
例三 Unique Paths II
题目描述:
给定m行n列的网格,有一个机器人从左上角(0,0)出发,每一次可以向下或者向右走一步,网格中有些地方有障碍,机器人不能通过障碍。问:有多少种不同的方式走到右下角?
代码如下:
#include
using namespace std;
int main()
{
int m,n;
scanf("%d %d",&m,&n); //输入行列数m,n
int f[m][n],dp[m][n];
int i,j,k;
for(i=0;i=0)
dp[i][j]+=dp[i-1][j];
if(j-1>=0)
dp[i][j]+=dp[i][j-1];
}
}
}
}
printf("%d\n",dp[m-1][n-1]);
return 0;
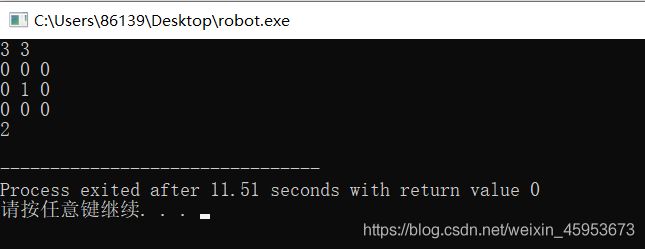
} 运行结果:
疑惑:
好像运行时间有点长???
例四 Jump Game
题目描述:
有n块石头分别在x轴的0,1,2,…,n-1位置上。一只青蛙在石头0,想跳到石头n-1上。如果一只青蛙在第i块石头上,它最多可以向右跳ai。问,青蛙能否跳到n-1?
代码如下:
#include
using namespace std;
int main()
{
int i,j,n;
scanf("%d",&n); //输入石头的数量
int a[n],f[n];
for(i=0;i=j)
{
f[j]=1;
break;
}
}
}
if(f[n-1]==1)
printf("Yes\n");
else
printf("No\n");
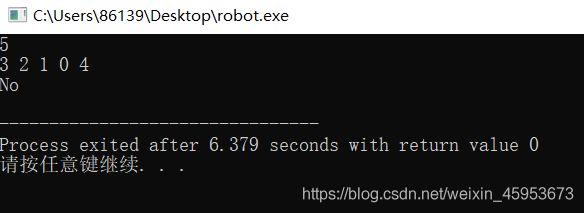
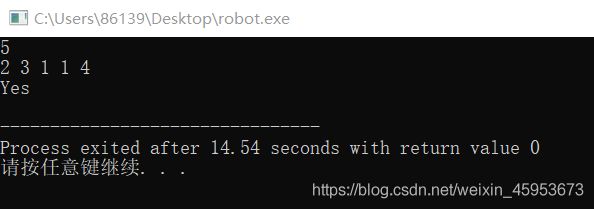
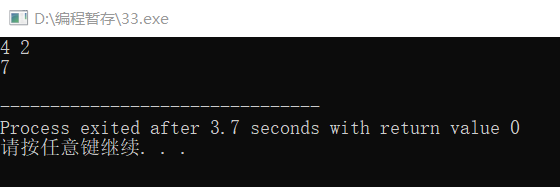
} 运行结果:
例五 Paint House
题目描述:
有一排N栋房子,每栋房子要漆成3种颜色中的一种:红、蓝、绿。任何两栋相邻的房子不能漆成同样的颜色第i栋房子染成红色、蓝色、绿色的花费分别是cost[i][0]、cost[i][1]、cost[i][2]。问:最少花多少钱漆这个房子?
代码如下:
#include
using namespace std;
int MIN(int m,int n,int t)
{
if(m>n)
m=n;
return m>t?t:m;
}
int main()
{
int N,i,j;
scanf("%d",&N); //输入房子数量
int cost[N][3],f[N+1][3]; //i表示前i栋 i表示前i栋 i表示前i栋 i表示前i栋
for(i=0;i 运行结果:
疑问:
运行速度一如既往得慢,希望大佬提出改进意见,感谢!
例六 Minimum Path Sum
题目描述:
给定m行n列的网格,每个格子(i,j)里都有一个非负数A[i][j],求一个从左上角(0,0)到右下角的路径,每一步只能向下或者向右走一步,使得路径上的格子里的数字之和最小,输出最小数字和。
代码如下:
#include
using namespace std;
int main()
{
int i,j,m,n;
scanf("%d %d",&m,&n);
int A[m][n],f[m][n];
for(i=0;i 运行结果:
优化代码:
滚动数组滚动数组滚动数组
#include
using namespace std;
int main()
{
int i,j,m,n;
scanf("%d%d",&m,&n);
int A[m][n],dp[2][n];
for(i=0;i
例七 数字三角形问题
题目描述:
给定一个由n行数字组成的数字三角形如下图所示。试设计一个算法,计算出从三角形的顶至底的一条路径,使该路径经过的数字总和最大。
对于给定的由n行数字组成的数字三角形,计算从三角形的顶至底的路径经过的数字和的最大值。
代码如下:
#include
using namespace std;
int main()
{
int n,i,j;
scanf("%d",&n);
int a[n][n];
memset(a,0,sizeof(a));
for(i=0;i=0;i--)
{
for(j=0;j<=i;j++)
{
dp[i][j]=max(dp[i+1][j],dp[i+1][j+1])+a[i][j];
}
}
printf("%d\n",dp[0][0]);
return 0;
}
#include
#include
#define MAX 101
using namespace std;
int n;
int D[MAX][MAX];
int maxsum[MAX][MAX];
int MaxSum(int i,int j)
{
if(maxsum[i][j]!=-1)
return maxsum[i][j];
if(i==n)
maxsum[i][j]=D[i][j];
else
{
int x=MaxSum(i+1,j);
int y=MaxSum(i+1,j+1);
maxsum[i][j]=max(x,y)+D[i][j];
}
return maxsum[i][j];
}
int main()
{
cin>>n;
int i,j;
for(i=1;i<=n;++i)
for(j=1;j<=i;++j)
{
cin>>D[i][j];
maxsum[i][j]=-1;
}
cout< 另附递归代码:
#include
#define MAX 101
using namespace std;
int n;
int a[MAX][MAX];
int maxsum[MAX][MAX]; //记录避免重复运算
int Maxsum(int i,int j)
{
if(maxsum[i][j]!=-1)
return maxsum[i][j];
if(i==n)
maxsum[i][j]=a[i][j];
else
maxsum[i][j]=max(Maxsum(i+1,j),Maxsum(i+1,j+1))+a[i][j];
return maxsum[i][j];
}
int main()
{
int i,j;
scanf("%d",&n); //三角形行数
for(i=1;i<=n;++i) //从第一行开始输入
for(j=1;j<=i;++j)
{
scanf("%d",&a[i][j]);
maxsum[i][j]=-1;
}
printf("%d\n",Maxsum(1,1));
return 0;
}
空间优化代码:
#include
#include
#define MAX 101
using namespace std;
int n;
int *maxsum;
int D[MAX][MAX];
int main()
{
cin>>n;
int i,j;
for(i=1;i<=n;++i)
for(j=1;j<=i;++j)
cin>>D[i][j];
maxsum=D[n];
for(i=n-1;i>=1;--i)
for(j=1;j<=i;++j)
maxsum[j]=max(maxsum[j],maxsum[j+1])+D[i][j];
cout< 运行结果:
例八 K好数
题目描述:
如果一个自然数N的K进制表示中任意的相邻的两位都不是相邻的数字,那么我们就说这个数是K好数。求L位K进制数中K好数的数目。
例如K = 4,L = 2的时候,所有K好数为11、13、20、22、30、31、33 共7个。由于这个数目很大,请你输出它对1000000007取模后的值。
代码如下:
#include
using namespace std;
#define NUM 1000000007;
int main()
{
int K,L;
int i,j,x,count=0;
scanf("%d%d",&K,&L);
int arr[L+1][K];
memset(arr,0,sizeof(arr));
for(i=0;i 运行结果:
例九 最长上升子序列
最长上升子序列(动态规划)——C++
例十 最长公共子序列
题目描述:
给出两个字符串,求出这样一个最长的公共子序列的长度:子序列中的每个字符都能在两个原字符串中找到,而且每个字符的先后顺序和原字符串中的先后顺序一致。
图解:
代码如下:
#include
#include
using namespace std;
char str1[1000];
char str2[1000];
int maxlength[1000][1000];
int main()
{
cin>>str1>>str2;
int length1=strlen(str1);
int length2=strlen(str2);
int i,j;
//maxlength[i][j]表示str1左边i个字符形成的子字符串和str2左边的j个字符形成的子字符串的最长公共子序列的长度
for(i=0;i<=length1;++i)
maxlength[i][0]=0;
for(j=0;j<=length2;++j)
maxlength[0][j]=0;
for(i=1;i<=length1;++i)
{
for(j=1;j<=length2;++j)
{
if(str1[i-1]==str2[j-1])
maxlength[i][j]=maxlength[i-1][j-1]+1;
else
maxlength[i][j]=max(maxlength[i-1][j],maxlength[i][j-1]);
}
}
cout< 运行结果:
例十一 最佳加法表达式
最佳加法表达式——动态规划详解——C++
例十二 神奇的口袋
题目描述:
有一个神奇的口袋,总的容积是40,用这个口袋可以变出一些物品,这些物品的总体积必须是40。John现在有n个想要得到的物品,每个物品的体积分别是 a1,a2……an。John可以从这些物品中选择一些,如果选出的物体的总体积是40,那么利用这个神奇的口袋,John就可以得到这些物品。现在的问题是,John有多少种不同的选择物品的方式。
输入:
输入的第一行是正整数n (1 <= n <= 20),表示不同的物品的数目。接下来的n行,每行有一个1到40之间的正整数,分别给出 a1,a2……an的值。
输出:
输出不同的选择物品的方式的数目。
代码如下:
#include
#include
using namespace std;
int N;
int a[20+1];
int Ways[40+1][20+1]; //Ways[i][j]表示从前j中物品中凑出体积i的方法数
int main()
{
cin>>N;
memset(Ways,0,sizeof(Ways));
for(int i=1;i<=N;++i) //下标从1开始
{
cin>>a[i];
Ways[0][i]=1;
}
Ways[0][0]=1;
for(int m=1;m<=40;++m)
{
for(int k=1;k<=N;++k)
{
Ways[m][k]=Ways[m][k-1];
if(m-a[k]>=0)
Ways[m][k]+=Ways[m-a[k]][k-1];
}
}
cout<
using namespace std;
int a[21];
int Ways(int m,int k)
{
if(m==0)
return 1;
if(k<=0)
return 0;
return Ways(m,k-1)+Ways(m-a[k],k-1);
}
int main()
{
int n;
cin>>n;
for(int i=1;i<=n;++i)
cin>>a[i];
cout< 运行结果:
例十三 0-1背包问题
0-1背包问题—动态规划+滚动数组—C++超详解
例十四 多重背包问题
https://blog.csdn.net/weixin_45953673/article/details/104932290
例十五 完全背包问题
完全背包问题——动态规划——C++详解