acm集训队课程设置--第八节课
acm集训队课程设置--第八节课
本节主要内容:关于数论的学习。
实现进制转换,最大公约数、最小公倍数求法等,还有大数相加减乘除,素数问题,斐波那契数列,容斥定理;
进制转换
n进制小数
将任意十进制正小数分别转换成2,3,4,5,6,7,8,9进制正小数,小数点后保留8位,并输出。
例如:若十进制小数为0.795,则输出:
十进制正小数 0.795000 转换成 2 进制数为: 0.11001011
十进制正小数 0.795000 转换成 3 进制数为: 0.21011011
十进制正小数 0.795000 转换成 4 进制数为: 0.30232011
十进制正小数 0.795000 转换成 5 进制数为: 0.34414141
十进制正小数 0.795000 转换成 6 进制数为: 0.44341530
十进制正小数 0.795000 转换成 7 进制数为: 0.53645364
十进制正小数 0.795000 转换成 8 进制数为: 0.62702436
十进制正小数 0.795000 转换成 9 进制数为: 0.71348853
以下代码提供了这个功能。其中,dTestNo表示待转的十进制小数。iBase表示进制数。
public class N进制小数 {
public static void fun(double dTestNo, int iBase) {
int[] iT = new int[8];
int iNo;
System.out.printf("十进制正小数 %f 转换成 %d 进制数为: ", dTestNo, iBase);
for (iNo = 0; iNo < 8; iNo++) {
dTestNo *= iBase;
iT[iNo] = (int)dTestNo ;
if(dTestNo>=1.0) dTestNo -= iT[iNo];
}
System.out.printf("0.");
for (iNo = 0; iNo < 8; iNo++)
System.out.printf("%d", iT[iNo]);
System.out.printf("\n");
}
public static void main(String[] args) {
double dTestNo = 0.795;
int iBase;
for (iBase = 2; iBase <= 9; iBase++)
fun(dTestNo, iBase);
System.out.printf("\n");
}
} 三进制转十进制
/* 三进制转十进制
下面的代码演示了如何把键盘输入的3进制数字转换为十进制。试完善之。
*/
import java.io.BufferedReader;
import java.io.InputStreamReader;
public class 三进制转十进制 {
public static void main(String[] args)throws Exception {
BufferedReader br = new BufferedReader(new InputStreamReader(System.in));
String s = br.readLine();
int n = 0;
for (int i = 0; i < s.length(); i++) {
char c = s.charAt(i);
if (c < '0' || c > '2')
throw new RuntimeException("Format error");
n = n*3 + (c-'0');
}
System.out.println(n);
}
} 最大公约数
int gcd(int da,int xiao)
{ int temp;
while (xiao!=0)
{
temp=da%xiao;
da=xiao;
xiao=temp;
}
return da;
}
快速幂递归实现:
int power(int a, int n){
int ans;
if(n==0) ans=1;
else
{ ans=power(a*a, n/2);
if(n%2==1) ans*=a;
}
return ans;
}
错排公式:
某人写了n封信,还有n个信封,如果所有的信都装错了信封,求共有多少种可能的情况?
例子:
礼上往来
发布时间: 2016年1月3日 19:13 最后更新: 2016年1月3日 19:15 时间限制: 1000ms 内存限制: 128M
每当节日来临,女友众多的xxx总是能从全国各地的女友那里收到各种礼物。
有礼物收到当然值得高兴,但回礼确是件麻烦的事!
无论多麻烦,总不好意思收礼而不回礼,那也不是xxx的风格。
现在,即爱面子又抠门的xxx想出了一个绝妙的好办法:他准备将各个女友送来的礼物合理分配,再回送不同女友,这样就不用再花钱买礼物了!
假设xxx的n个女友每人送他一个礼物(每个人送的礼物都不相同),现在他需要合理安排,再回送每个女友一份礼物,重点是,回送的礼物不能是这个女友之前送他的那个礼物,不然,xxx可就摊上事了,摊上大事了......
现在,xxx想知道总共有多少种满足条件的回送礼物方案呢?
输入数据第一行是个正整数T,表示总共有T组测试数据(T <= 100);
每组数据包含一个正整数n,表示叽叽哥的女友个数为n( 1 <= n <= 100 )。
请输出可能的方案数,因为方案数可能比较大,请将结果对10^9 + 7 取模后再输出。
每组输出占一行。
3 1 2 4
0 1 9
#include
#define LL long long
using namespace std;
const LL mod = 1e9+7;
LL d[105];
inline void init()
{
d[0] = d[1] = 0; d[2] = 1;
for(int i = 3; i <= 100; ++i)
d[i] = (i-1)*((d[i-1]+d[i-2])%mod)%mod;
}
int main()
{
int t, n;
cin >> t; init();
for(int _ = 1; _ <= t; ++_)
{
cin >> n;
cout << d[n] << endl;
}
return 0;
} 容斥原理
容斥原理描述如下:
说大白话就是求几个集合的并集,要计算几个集合并集的大小,我们要先将所有单个集合的大小计算出来,然后减去所
有两个集合相交的部分,再加上所有三个集合相交的部分,再减去所有四个集合相交的部分...依此类推,一直计算到
所有集合相交的部分。
最简单的就是两个集合的并集:
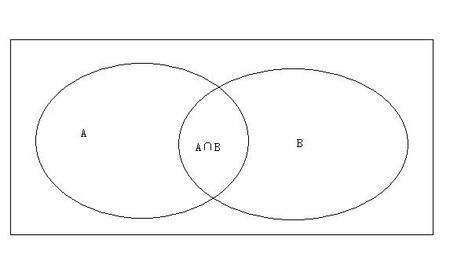
所以数学公式就可以表示为 |A∪B|=|A|+|B|-|A∩B|。
对于三个集合,数学公式为|A∪B∪C|=|A|+|B|+|C|-|A∩B|-|A∩C|-|B∩C|+|A∩B∩C|。
常用方法有两种:递归法和二进制枚举法。
递归法是利用dfs的思想进行搜索,检索每一种方案进行容斥。
二进制枚举的方法最大的好处是能够枚举出所有元素组合的不同集合。假设一个集合的元素有m个,则对于m长的二进
制数来说就有m个1或0的位置,对于每一个1就对应一个元素。
整个二进制枚举完就是所有子集,从0到2^m就行。[0, 2^m)
题意:给定一个数n,数列m个数,求这小于n的数中,有多少个数满足能被这m个数中任意一个数整除。
思路:1~n之间有多少个能被x整除的数,公式为n/x,题目中要求小于n,所以(n-1)/x。
可以递归法求,需要保存中间态重叠x次的最小公倍数lcm,符合题意的数有(n-1)/lcm个,根据k表示重叠的次数进行或者加上,或者减去。
也可以用二进制枚举法,将符合条件的m个数,看作m位,每位是0或者是1,那么一共有2^m种状态,只要判断一下每一个状态有多少个1,也就是有多少个数(重叠多少次),记为k,每一个1代表哪几个具体的数,求这几个数的最小公倍数,然后(n-1)/lcm, 利用k的值来判断应该减去还是加上即可。
#include
using namespace std;
int n, m, num[15], ans, tot, x;
int gcd(int a, int b)
{
if(a%b == 0) return b;
return gcd(b, a%b);
}
void dfs(int pos, int pre_lcm, int k)
{
for(int i = pos+1; i < tot; ++i)
{
int lcm = pre_lcm/gcd(num[i], pre_lcm)*num[i];
if(k&1) ans += (n-1)/lcm;
else ans -= (n-1)/lcm;
dfs(i, lcm, k+1);
}
}
int main()
{
while(~scanf("%d %d", &n, &m))
{
ans = 0; tot = 1;
for(int i = 1; i <= m; ++i)
{
scanf("%d", &x);
if(x > 0 && x < n) num[tot++] = x;
}
dfs(0, 1, 1);
printf("%d\n", ans);
}
return 0;
} #include
using namespace std;
int n, m, x, k, tot, up, t, pos, lcm, ans, num[15];
int gcd(int a, int b)
{
if(a%b == 0) return b;
return gcd(b, a%b);
}
int main()
{
while(~scanf("%d %d", &n, &m))
{
tot = 1; ans = 0;
for(int i = 1; i <= m; ++i)
{
scanf("%d", &x);
if(x > 0 && x < n) num[tot++] = x;
}
up = (1<<(tot-1));
for(int i = 1; i < up; ++i)
{
t = i, k = 0, pos = 1; lcm = 1;
while(t)
{
if(t&1)
{
lcm = num[pos]/gcd(lcm, num[pos])*lcm;
++k;
}
t >>= 1; ++pos;
}
if(k&1) ans += (n-1)/lcm;
else ans -= (n-1)/lcm;
}
printf("%d\n", ans);
}
return 0;
}