《Python》SciPy——数值计算库

    SciPy函数库在NumPy库的基础上增加了众多的数学、科学以及工程计算中常用的库函数。例如线性代数、常微分方程数值求解、信号处理、图像处理、稀疏矩阵等等。作为入门介绍，让我们看看如何用SciPy进行插值处理、信号滤波以及用C语言加速计算。

一、最小二乘拟合

    假设有一组实验数据(x[i], y[i])，我们知道它们之间的函数关系:y = f(x)，通过这些已知信息，需要确定函数中的一些参数项。例如，如果f是一个线型函数f(x) = k*x+b，那么参数k和b就是我们需要确定的值。如果将这些参数用 p 表示的话，那么我们就是要找到一组 p 值使得如下公式中的S函数最小$$S(p)=\sum _{i=1}^m[y_i-f(x_i，p){]}^2$$
这种算法被称之为最小二乘拟合(Least-square fitting)。

• leastsq函数：
  scipy中的子函数库optimize已经提供了实现最小二乘拟合算法的函数leastsq。

leastsq函数使用实例：

 # -*- coding: utf-8 -*-
import numpy as np
from scipy.optimize import leastsq
import pylab as pl

def func(x, p):
"""
数据拟合所用的函数: A*sin(2*pi*k*x + theta)
"""
A, k, theta = p
return A*np.sin(2*np.pi*k*x+theta)

def residuals(p, y, x):
"""
实验数据x, y和拟合函数之间的差，p为拟合需要找到的系数
"""
return y - func(x, p)

x = np.linspace(0, -2*np.pi, 100)
A, k, theta = 10, 0.34, np.pi/6 # 真实数据的函数参数
y0 = func(x, [A, k, theta]) # 真实数据
y1 = y0 + 2 * np.random.randn(len(x)) # 加入噪声之后的实验数据

p0 = [7, 0.2, 0] # 第一次猜测的函数拟合参数

# 调用leastsq进行数据拟合
# residuals为计算误差的函数
# p0为拟合参数的初始值
# args为需要拟合的实验数据
plsq = leastsq(residuals, p0, args=(y1, x))

print u"真实参数:", [A, k, theta]
print u"拟合参数", plsq[0] # 实验数据拟合后的参数

pl.plot(x, y0, label=u"真实数据")
pl.plot(x, y1, label=u"带噪声的实验数据")
pl.plot(x, func(x, plsq[0]), label=u"拟合数据")
pl.legend()
pl.show()

    这个例子中我们要拟合的函数是一个正弦波函数，它有三个参数 A, k, theta ，分别对应振幅、频率、相角。假设我们的实验数据是一组包含噪声的数据 x, y1，其中y1是在真实数据y0的基础上加入噪声的到了。
    通过leastsq函数对带噪声的实验数据x, y1进行数据拟合，可以找到x和真实数据y0之间的正弦关系的三个参数： A, k, theta。

输出结果：
真实参数: [10, 0.34000000000000002, 0.52359877559829882]
拟合参数 [-9.84152775 0.33829767 -2.68899335]

我们看到拟合参数虽然和真实参数完全不同，但是由于正弦函数具有周期性，实际上拟合参数得到的函数和真实参数对应的函数是一致的。

二、函数最小值

    optimize库提供了几个求函数最小值的算法：fmin, fmin_powell, fmin_cg, fmin_bfgs。
    对于一个离散的线性时不变系统h, 如果它的输入是x，那么其输出y可以用x和h的卷积表示：
                                    y = x ∗ h
    现在的问题是如果已知系统的输入x和输出y，如何计算系统的传递函数h；或者如果已知系统的传递函数h和系统的输出y，如何计算系统的输入x。这种运算被称为反卷积运算，是十分困难的，特别是在实际的运用中，测量系统的输出总是存在误差的。
    用fmin计算反卷积，这种方法只能用在很小规模的数列之上，因此没有很大的实用价值，不过用来评价fmin函数的性能还是不错的。

三、非线性方程组求解

    optimize库中的fsolve函数可以用来对非线性方程组进行求解。

• fsolve函数：
  基本调用形式为：fsolve(func, x0)
  func(x)是计算方程组误差的函数，它的参数x是一个矢量，表示方程组的各个未知数的一组可能解，func返回将x代入方程组之后得到的误差；x0为未知数矢量的初始值。如果要对如下方程组进行求解的话：
                                      f1(u1,u2,u3) = 0
                                      f2(u1,u2,u3) = 0
                                      f3(u1,u2,u3) = 0
  那么func可以如下定义：

def func(x):
u1,u2,u3 = x
return [f1(u1,u2,u3), f2(u1,u2,u3), f3(u1,u2,u3)]

fsolve函数使用实例：
求解下列方程：
5x1 + 3 = 0
4x0x0 - 2sin(x1x2) = 0
x1x2 - 1.5 = 0
调用fsolve函数来求解此方程

from scipy.optimize import fsolve
from math import sin,cos

def f(x):
x0 = float(x[0])
x1 = float(x[1])
x2 = float(x[2])
return [
5*x1+3,
4*x0*x0 - 2*sin(x1*x2),
x1*x2 - 1.5]

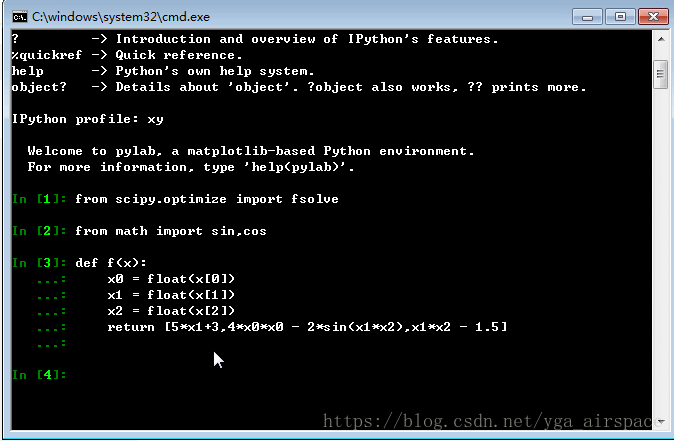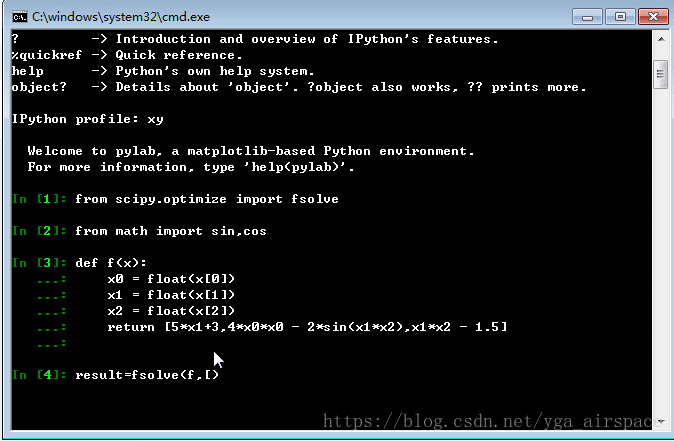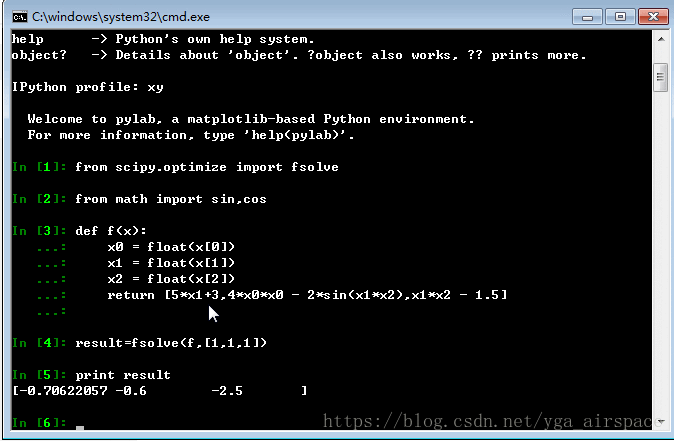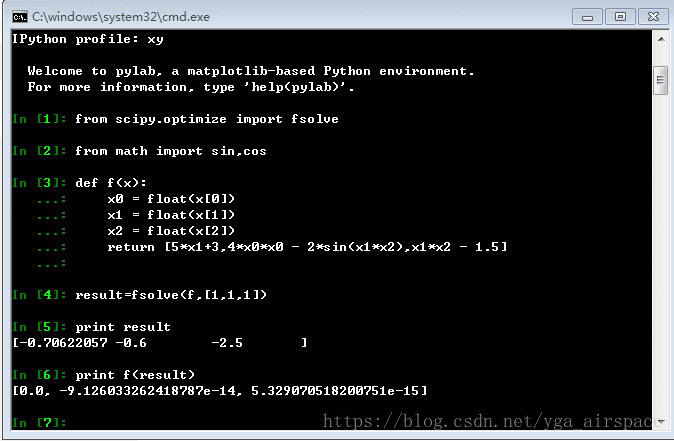
result = fsolve(f, [1,1,1])

print result
print f(result)

四、 B-Spline样条曲线

    interpolate库提供了许多对数据进行插值运算的函数。

使用直线和B-Spline对正弦波上的点进行插值的实例：

# -*- coding: utf-8 -*-
import numpy as np
import pylab as pl
from scipy import interpolate

x = np.linspace(0, 2*np.pi+np.pi/4, 10)
y = np.sin(x)

x_new = np.linspace(0, 2*np.pi+np.pi/4, 100)
f_linear = interpolate.interp1d(x, y)
tck = interpolate.splrep(x, y)
y_bspline = interpolate.splev(x_new, tck)

pl.plot(x, y, "o", label=u"原始数据")
pl.plot(x_new, f_linear(x_new), label=u"线性插值")
pl.plot(x_new, y_bspline, label=u"B-spline插值")
pl.legend()
pl.show()

输出结果：

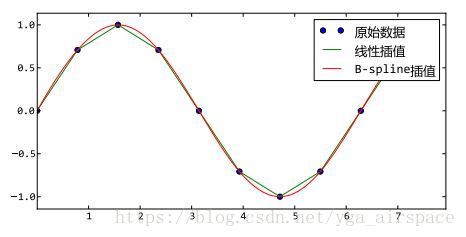
在这段程序中，通过interp1d函数直接得到一个新的线性插值函数。而B-Spline插值运算需要先使用splrep函数计算出B-Spline曲线的参数，然后将参数传递给splev函数计算出各个取样点的插值结果。

五、 数值积分

    数值积分是对定积分的数值求解，例如可以利用数值积分计算某个形状的面积。

• trapz函数：
  当计算的是以x,y为顶点坐标的折线与X轴所夹的面积。同样的分割点数，trapz函数的结果更加接近精确值一些。

trapz函数使用实例：
下面让我们来计算半径为1的半圆的面积

import numpy as np

def half_circle(x):
return (1-x**2)**0.5
N = 10000
x = np.linspace(-1, 1, N)
y = half_circle(x)
np.trapz(y, x) * 2  # 面积的两倍

• quad函数：
  如果我们调用scipy.integrate库中的quad函数来计算半径为1的半圆的面积，将会得到非常精确的结果。

quad函数使用实例：

from scipy import integrate

def half_circle(x):
return (1-x**2)**0.5

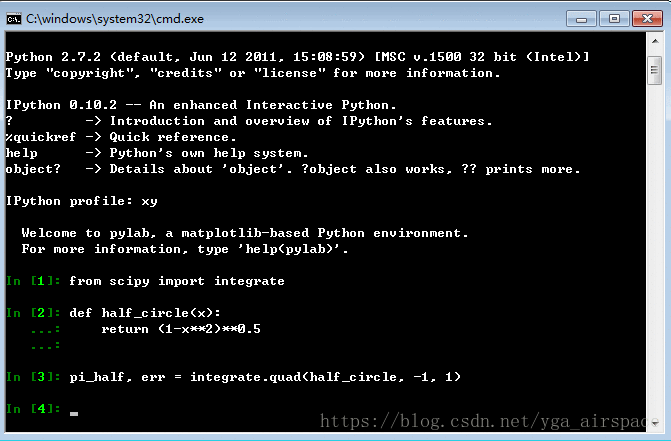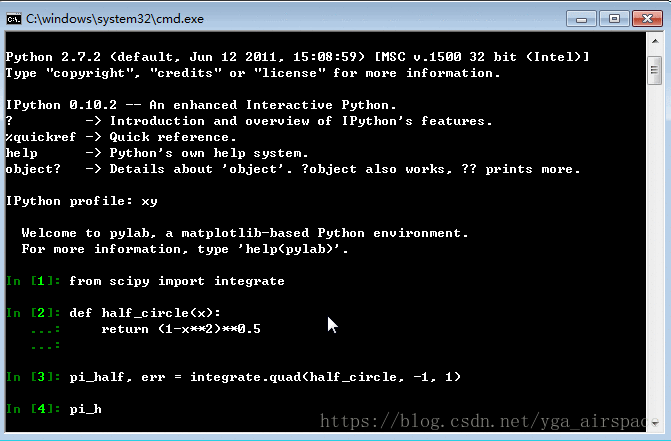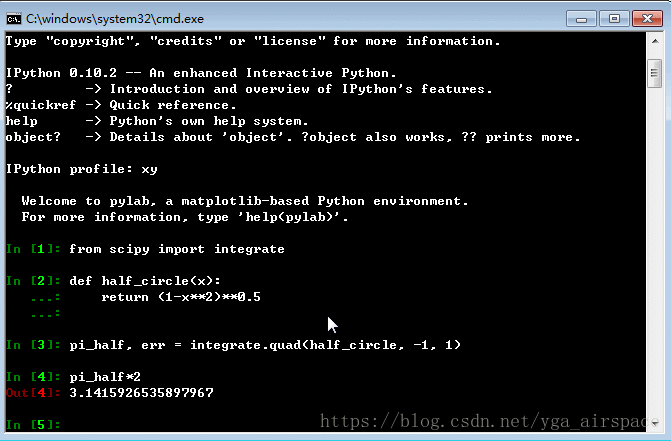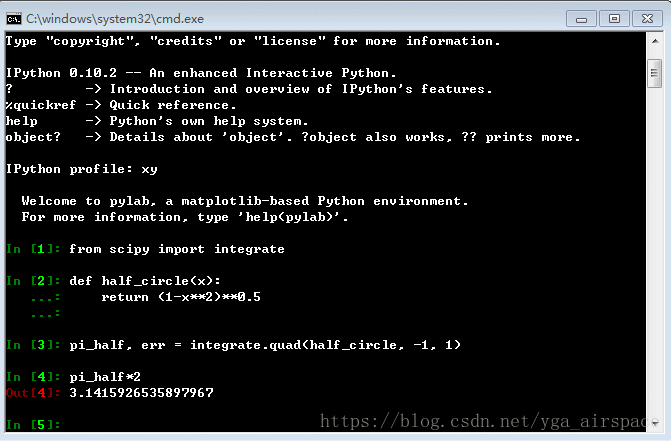
pi_half, err = integrate.quad(half_circle, -1, 1)
pi_half*2

六、 解常微分方程组

    scipy.integrate库提供了数值积分和常微分方程组求解算法odeint。

• odeint算法：
  下面让我们用odeint计算洛仑兹吸引子的轨迹。洛仑兹吸引子由下面的三个微分方程定义：
                                  dx/dt = σ(y − x)
                                  dy/dt = x(ρ − z) − y
                                  dz/dt = xy − βz
  这三个方程定义了三维空间中各个坐标点上的速度矢量。从某个坐标开始沿着速度矢量进行积分，就可以计算出无质量点在此空间中的运动轨迹。其中 σ, ρ, β 为三个常数，不同的参数可以计算出不同的运动轨迹： x(t), y(t), z(t)。 当参数为某些值时，轨迹出现馄饨现象：即微小的初值差别也会显著地影响运动轨迹。

odeint算法使用实例：

# -*- coding: utf-8 -*-
from scipy.integrate import odeint
import numpy as np

def lorenz(w, t, p, r, b):
# 给出位置矢量w，和三个参数p, r, b计算出
# dx/dt, dy/dt, dz/dt的值
x, y, z = w
# 直接与lorenz的计算公式对应
return np.array([p*(y-x), x*(r-z)-y, x*y-b*z])

t = np.arange(0, 30, 0.01) # 创建时间点
# 调用ode对lorenz进行求解, 用两个不同的初始值
track1 = odeint(lorenz, (0.0, 1.00, 0.0), t, args=(10.0, 28.0, 3.0))
track2 = odeint(lorenz, (0.0, 1.01, 0.0), t, args=(10.0, 28.0, 3.0))

# 绘图
from mpl_toolkits.mplot3d import Axes3D
import matplotlib.pyplot as plt

fig = plt.figure()
ax = Axes3D(fig)
ax.plot(track1[:,0], track1[:,1], track1[:,2])
ax.plot(track2[:,0], track2[:,1], track2[:,2])
plt.show()

输出结果：

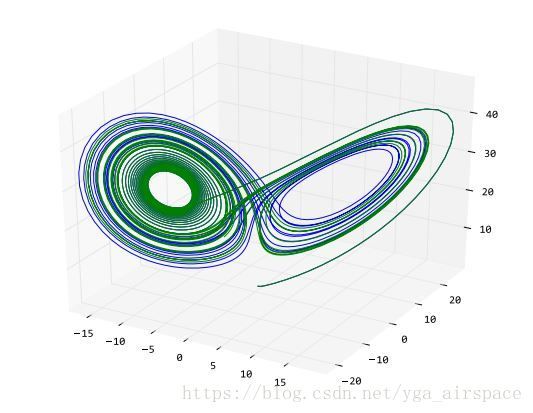
我们看到即使初始值只相差0.01，两条运动轨迹也是完全不同的。
在程序中先定义一个“lorenz函数”，它的任务是计算出某个位置的各个方向的微分值，这个计算直接根据洛仑兹吸引子的公式得出。然后调用odeint，对微分方程求解，odeint有许多参数，这里用到的四个参数分别为：

1. lorenz， 它是计算某个位移上的各个方向的速度(位移的微分)
2. (0.0, 1.0, 0.0)，位移初始值。计算常微分方程所需的各个变量的初始值
3. t， 表示时间的数组，odeint对于此数组中的每个时间点进行求解，得出所有时间点的位置
4. args， 这些参数直接传递给lorenz函数，因此它们都是常量

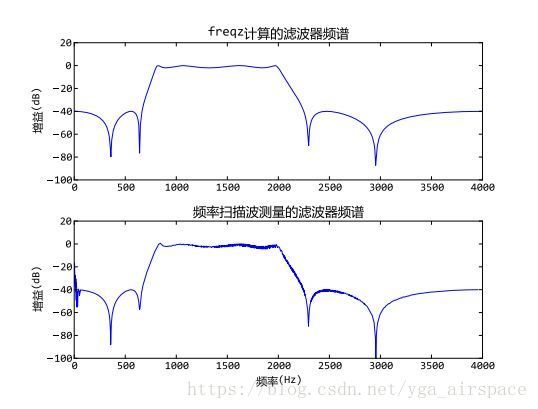
七、 滤波器设计

    scipy.signal库提供了许多信号处理方面的函数。

• signal库：
  让我们利用signal库设计滤波器，查看滤波器的频率响应，以及如何使用滤波器对信号进行滤波。

signal库使用实例：

import scipy.signal as signal

#设计一个带通IIR滤波器
b, a = signal.iirdesign([0.2, 0.5], [0.1, 0.6], 2, 40)
#通过调用freqz计算所得到的滤波器的频率响应
w, h = signal.freqz(b, a)
#计算h的增益特性，并转换为dB度量。由于h中存在幅值几乎为0的值，因此先用clip函数对其裁剪之后，再调用对数函数，避免计算出错
power = 20*np.log10(np.clip(np.abs(h), 1e-8, 1e100))
#通过下面的语句可以绘制出滤波器的增益特性图，这里假设取样频率为8kHz
pl.plot(w/np.pi*4000, power)
#为了调用chirp函数以产生频率扫描波形的数据，首先需要产生一个等差数组代表取样时间，下面的语句产生2秒钟取样频率为8kHz的取样时间数组
t = np.arange(0, 2, 1/8000.0)
#然后调用chirp得到2秒钟的频率扫描波形的数据
sweep = signal.chirp(t, f0=0, t1 = 2, f1=4000.0)
#通过调用lfilter函数计算sweep波形经过带通滤波器之后的结果
out = signal.lfilter(b, a, sweep)
#为了和系统的增益特性图进行比较，需要获取输出波形的包络，因此下面先将输出波形数据转换为能量值
out = 20*np.log10(np.abs(out))
#为了计算包络，找到所有能量大于前后两个取样点(局部最大点)的下标
index = np.where(np.logical_and(out[1:-1] > out[:-2], out[1:-1] > out[2:]))[0] + 1
#最后将时间转换为对应的频率，绘制所有局部最大点的能量值
pl.plot(t[index]/2.0*4000, out[index] )

输出结果：

八、 用Weave嵌入C语言

    Python作为动态语言其功能虽然强大，但是在数值计算方面有一个最大的缺点：速度不够快。在Python级别的循环和计算的速度只有C语言程序的百分之一。因此才有了NumPy, SciPy这样的函数库，将高度优化的C、Fortran的函数库进行包装，以供Python程序调用。如果这些高度优化的函数库无法实现我们的算法，必须从头开始写循环、计算的话，那么用Python来做显然是不合适的。因此SciPy提供了快速调用C++语言程序的方法——Weave。

Weave使用实例：

# -*- coding: utf-8 -*-
import scipy.weave as weave
import numpy as np
import time

def my_sum(a):
n=int(len(a))
code="""
int i;
double counter;
counter =0;
for(i=0;i

err=weave.inline(
code,['a','n'],
type_converters=weave.converters.blitz,
compiler="gcc"
)
return err

a = np.arange(0, 10000000, 1.0)
# 先调用一次my_sum，weave会自动对C语言进行编译，此后直接运行编译之后的代码
my_sum(a)

start = time.clock()
for i in xrange(100):
my_sum(a) # 直接运行编译之后的代码
print "my_sum:", (time.clock() - start) / 100.0

start = time.clock()
for i in xrange(100):
np.sum( a ) # numpy中的sum，其实现也是C语言级别
print "np.sum:", (time.clock() - start) / 100.0

start = time.clock()
print sum(a) # Python内部函数sum通过数组a的迭代接口访问其每个元素，因此速度很慢
print "sum:", time.clock() - start

输出结果：
my_sum: 0.0294527349146
np.sum: 0.0527649547638
sum: 9.11022322669

---

    从上述实验结果可以看到用Weave编译的C语言程序比numpy自带的sum函数还要快。而Python的内部函数sum使用数组的迭代器接口进行运算，因此速度是Python语言级别的，只有Weave版本的1/300。
    weave.inline函数的第一个参数为需要执行的C++语言代码，第二个参数是一个列表，它告诉weave要把Python中的两个变量a和n传递给C++程序，注意我们用字符串表示变量名。converters.blitz是一个类型转换器，将numpy的数组类型转换为C++的blitz类。C++程序中的变量a不是一个数组，而是blitz类的实例，因此它使用a(i)获得其各个元素的值，而不是用a[i]。最后我们通过compiler参数告诉weave要采用gcc为C++编译器。如果你安装的是python(x,y)的话，gcc(mingw32)也一起安装好了，否则你可能需要手工安装gcc编译器或者微软的Visual C++。
    Note: 在我的电脑上，虽然安装了Visual C++ 2008 Express，但仍然提示找不到合适的Visual C++编译器。似乎必须使用编译Python的编译器版本。因此还是用gcc来的方便。