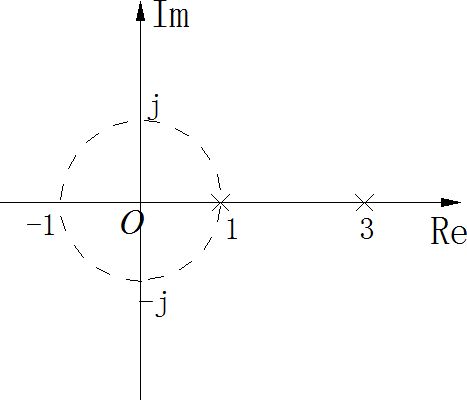2020年春季学期信号与系统课程作业参考答案-第十二次作业

信号与系统第十二次作业参考答案  

 

※ 第一题

---

利用Laplace变换求解下列微分方程：
（1）$$\frac{d^2}{d{t}^2}y\left(t\right)+2\frac{d}{dt}y\left(t\right)+y\left(t\right)=\delta \left(t\right)+2{\delta }^{\prime }\left(t\right)$$
$$y\left(0_{-}\right)=1,y^{\prime }\left(0_{-}\right)=2$$
（2）$$\frac{d^2}{d{t}^2}y\left(t\right)+5\frac{d}{dt}y\left(t\right)+6y\left(t\right)=3x\left(t\right)$$
$$x\left(t\right)=e^{-t}u\left(t\right),y\left(0_{-}\right)=0,y^{\prime }\left(0_{-}\right)=1$$

---

■ 求解：

（1）解答： 对微分方程两边进行Laplace变换，根据Laplace变换的微分定理，可将系统的初始条件代入方程：
$$s^{2}Y\left(s\right)-sy\left(0_{-}\right)-y^{\prime }\left(0_{-}\right)+2\left[sY\left(s\right)-y\left(0_{-}\right)\right]+Y\left(s\right)=1+2s$$

$$s^{2}Y\left(s\right)-s-2+2\left[sY\left(s\right)-1\right]+Y\left(s\right)=1+2s$$

$$\left(s^2+2s+1\right)Y\left(s\right)=3s+5$$

$$Y\left(s\right)=\frac{5+3s}{s^2+2s+1}$$

>>ilaplace((3*s+5)/(s*s+2*s+1))'
ans=3*exp(-t)+2*t*exp(-t)

$$y\left(t\right)=3e^{-t}+2t\cdot e^{-t},t\ge 0$$

（2）解答： 对微分方程两边进行Laplace变换，根据Laplace变换的微分定理，可将系统的初始条件代入方程：

$$s^{2}Y\left(s\right)-sy\left(0_{-}\right)-y^{\prime }\left(0_{-}\right)+5\left[sY\left(s\right)-y\left(0_{-}\right)\right]+6Y\left(s\right)=3X\left(s\right)$$

$$X\left(s\right)=\frac{1}{s+1}$$

$$\left(s^2+5s+6\right)Y\left(s\right)=\frac{1}{s+1}+1$$

$$Y\left(s\right)=\frac{s+2}{\left(s+1\right)\left(s^2+5s+6\right)}$$

>>ilaplace((s+2)/((s+1)*(s*s+5*s+6)))'
ans=exp(-t)/2 -exp(-3*t)/2

$$y\left(t\right)=\frac{1}{2}{e}^{-t}-\frac{1}{2}{e}^{-3t},t\ge 0$$

 

※ 第二题

---

利用单边z变换求解下列差分方程，并求出零输入响应和零状态响应。
（1）$$y\left[n\right]+3y\left[n-1\right]=x\left[n\right],x\left[n\right]={\left(\frac{1}{2}\right)}^n\cdot u\left[n\right],y\left[-1\right]=1$$
（2）$$y\left[n\right]-\frac{1}{2}y\left[n-1\right]=x\left[n\right]-\frac{1}{2}x\left[n-1\right],x\left[n\right]=u\left[n\right],y\left[-1\right]=1$$

---

■ 求解：

（1）解答： 方程两边同时进行z变换：
$$Y\left(z\right)+3z^{-1}Y\left(z\right)+3\cdot y\left[-1\right]=X\left(z\right)$$$$\left(1+3z^{-1}\right)Y\left(z\right)=\frac{z}{z-\frac{1}{2}}-3$$$$Y\left(z\right)=\frac{z\left(-2z+\frac{3}{2}\right)}{\left(z-\frac{1}{2}\right)\left(z+3\right)}=\frac{\frac{1}{7}z}{z-\frac{1}{2}}+\frac{-\frac{15}{7}z}{z+3}$$
$$y\left[n\right]=\frac{1}{7}{\left(\frac{1}{2}\right)}^{n}u\left[n\right]-\frac{15}{7}{\left(-3\right)}^{n}u\left[n\right]$$

零输入响应：
$$Y_{zi}\left(z\right)=\frac{-3}{1+3z^{-1}}=\frac{-3z}{z+3}$$$$y_{zi}\left[n\right]=-3{\left(-3\right)}^n\cdot u\left[n\right]={\left(-3\right)}^{n+1}u\left[n\right]$$

零状态响应：
$$Y_{zs}\left(z\right)=\frac{z^2}{\left(z-\frac{1}{2}\right)\left(z+3\right)}=\frac{\frac{1}{7}z}{z-\frac{1}{2}}+\frac{\frac{6}{7}z}{z+3}$$$$y_{zs}\left[n\right]=\frac{1}{7}{\left(\frac{1}{2}\right)}^{n}u\left[n\right]+\frac{6}{7}{\left(-3\right)}^{n}u\left[n\right]$$

（2）解答： 方程两边同时进行z变换：
$$Y\left(z\right)-\frac{1}{2}{z}^{-1}Y\left(z\right)-\frac{1}{2}y\left[-1\right]=\left(1-\frac{1}{2}{z}^{-1}\right)\cdot \frac{z}{z-1}$$$$Y\left(z\right)=\frac{z\left(\frac{3}{2}z-1\right)}{\left(z-1\right)\left(z-\frac{1}{2}\right)}=\frac{z}{z-1}+\frac{\frac{1}{2}}{z-\frac{1}{2}}$$$$y\left[n\right]=u\left[n\right]+{\left(\frac{1}{2}\right)}^{n+2}u\left[n\right]$$

系统的零输入响应为：
$$Y_{zi}\left(z\right)=\frac{\frac{1}{2}z}{z-\frac{1}{2}}$$$$y_{zi}\left[n\right]={\left(\frac{1}{2}\right)}^{n+1}u\left[n\right]$$

系统的零状态响应为：
$$Y_{zs}\left(z\right)=\frac{z}{z-1}$$$$y_{zs}\left[n\right]=u\left[n\right]$$

 

※ 第三题

---

设激励$x\left(t\right)=e^{-t}$时，系统的零状态响应为：$$y\left(t\right)=\frac{1}{2}{e}^{-t}-e^{-2t}+2e^{-3t}$$
求系统的单位脉冲响应信号$h\left(t\right)$。

---

■ 求解：

分别对输入信号$x\left(t\right)$和系统的零状态响应$y\left(t\right)$进行Laplace变换：
$$X\left(s\right)=LT\left[e^{-t}\cdot u\left(t\right)\right]=\frac{1}{s+1}$$

$$Y\left(s\right)=LT\left[\frac{1}{2}{e}^{-t}-e^{-2t}+2e^{-3t}\right]=\frac{1}{2}\frac{1}{s+1}-\frac{1}{s+2}+\frac{2}{s+3}$$

$$=\frac{\frac{3}{2}{s}^2+\frac{9}{2}s+4}{\left(s+1\right)\left(s+2\right)\left(s+3\right)}$$

根据线性是不变系统的性质，系统的零状态输出等于系统的输入信号与系统的单位冲击响应信号的卷积：$$y\left(t\right)=x\left(t\right)\ast h\left(t\right)$$

根据Laplace变换的卷积定理：$$Y\left(s\right)=X\left(s\right)\cdot H\left(s\right)$$

因此：$$H\left(s\right)=\frac{Y\left(s\right)}{X\left(s\right)}=\frac{\frac{3}{2}{s}^2+\frac{9}{2}s+4}{{\left(s+1\right)}^2\left(s+2\right)\left(s+3\right)}$$

>>ilaplace((1.5*s*s+4.5*s+4)/((s+1)^2*(s+2)*(s+3)))'
ans=exp(-2*t)-exp(-3*t)+(t*exp(-t))/2

则系统的单位冲击响应信号$h\left(t\right)$等于：$$h\left(t\right)=e^{-2t}-e^{-3t}+\frac{1}{2}t\cdot e^{-t},t\ge 0$$

 

※ 第四题

---

画出$$X\left(z\right)=\frac{-3z^{-1}}{1-4z^{-1}+3z^{-2}}$$
的零极点图，在下列三种收敛域的情况下，求出各自对应的序列：
（1） $\left|z\right|>3$
（2） $\left|z\right|<1$
（3） $1<\left|z\right|<3$

---

■ 求解：

$$X\left(z\right)=\frac{-3z}{z^2-4z+3}=\frac{-3z}{\left(z-1\right)\left(z-3\right)}=\frac{\frac{3}{2}z}{z-1}+\frac{\frac{-3}{2}z}{z-3}$$

（1） $$x\left[n\right]=\frac{3}{2}u\left[n\right]-\frac{3}{2}{3}^n\cdot u\left[n\right]$$

（2） $$x\left[n\right]=-\frac{3}{2}u\left[-n-1\right]+\frac{3}{2}{3}^n\cdot u\left[-n-1\right]$$

（3） $$x\left[n\right]=\frac{3}{2}u\left[n\right]+\frac{3}{2}{3}^n\cdot u\left[-n-1\right]$$

 

※ 第五题

---

给定实数序列$x\left[n\right]$及其z变换的表达式$X\left(z\right)$。请证明：$$X\left(z\right)=X^{\ast }\left(z^{\ast }\right)$$

---

■ 证明：

$$X\left(z\right)=\sum _{n=-\infty }^{\infty }x\left[n\right]\cdot z^{-n}$$

$$X\left(z^{\ast }\right)=\sum _{n=-\infty }^{\infty }x\left[n\right]\cdot {\left(z^{\ast }\right)}^{-n}={\left(\sum _{n=-\infty }^{\infty }x\left[n\right]\cdot z^{-n}\right)}^{\ast }=X^{\ast }\left(z\right)$$

两边再取共轭，原题得证。

 

※ 第六题

---

已知：$$X\left(z\right)=\ln \left(1+\frac{a}{z}\right),\left(\left|z\right|>\left|a\right|\right)$$
求对应的序列$x\left[n\right]$。

---

■ 求解：

方法1：
$$X\left(z\right)=\sum _{n=0}^{\infty }x\left[n\right]z^{-n}$$$$X^{\prime }\left(z\right)=\sum _{n=0}^{\infty }\left(-n\right)x\left[n\right]z^{-n-1}$$$$z\cdot X^{\prime }\left(z\right)=\sum _{n=0}^{\infty }\left\{-n\cdot x\left[n\right]\right\}{z}^{-n}$$$$-n\cdot x\left[n\right]=Z{T}^{-1}\left[z\cdot X^{\prime }\left(z\right)\right]$$$$x\left[n\right]=\frac{1}{-n}\cdot Z{T}^{-1}\left[z\cdot X^{\prime }\left(z\right)\right]$$
$$\frac{d}{dz}X\left(z\right)=\frac{d}{dz}\ln \left(\frac{z+a}{z}\right)=\frac{z}{z+a}\cdot \frac{d}{dz}\left(\frac{z+a}{z}\right)$$$$=\frac{z}{z+a}\cdot \frac{z-\left(z+a\right)}{z^2}=\frac{-a}{z\left(z+a\right)}$$
$$z\cdot \frac{d}{dz}X\left(z\right)=\frac{-az}{z\left(z+a\right)}=\frac{-a}{z+a}$$
$$Z{T}^{-1}\left[z\cdot X^{\prime }\left(z\right)\right]={\left(-a\right)}^n\cdot u\left[n-1\right]$$
$$x\left[n\right]=\frac{{\left(-a\right)}^n}{-n}\cdot u\left[n-1\right]$$

>>iztrans(log(1+a/z))'
ans=((-1)^(n-1)*a^n*(heaviside(n-1)+kroneckerDelta(n-1,0)/2))/n

方法2：
利用对数进行Taylor展开：

>>taylor(log(1-x),'Order',10)'
ans=-x^9/9 -x^8/8 -x^7/7 -x^6/6 -x^5/5 -x^4/4 -x^3/3 -x^2/2 -x

$$\ln \left(1-x\right)=-x-\frac{x^2}{2}-\frac{x^3}{3}-\frac{x^4}{4}-....=\sum _{n=1}^{\infty }-\frac{x^n}{n}$$
$$\ln \left(1-\frac{1}{z}\right)=\sum _{n=1}^{\infty }-\frac{z^{-n}}{n}$$