非凸问题的求解方法以及连续凸逼近SCA(Successive Convex Approximation)方法
非凸问题的求解方法以及连续凸逼近SCA(Successive Convex Approximation)方法
- 非凸问题的转换形式
针对形如下式的函数:
min x ∈ X V ( x ) = F ( x ) + G ( x ) \min\limits_{{\bf{x}}\in X} V(x)=F(x)+G(x) x∈XminV(x)=F(x)+G(x);[1]
其中F为光滑的(不一定convex),G是convex的但是可能不可微,且存在:对于n维实矢量空间,有 X = X 1 × . . . × X N X=X_1 \times...\times X_N X=X1×...×XN; x = ( x 1 , . . . , x N ) \bf{x} =(x_1,...,x_N) x=(x1,...,xN); 且 G ( x ) = ∑ i = 1 N g i ( x i ) G(x)=\sum\limits_{i = 1}^N g_i(\bf{x_i}) G(x)=i=1∑Ngi(xi).
具体实例求解方法:
1)当 G ( x ) = 0 G({\bf{x}})=0 G(x)=0, 该问题简化为一个具有凸约束的光滑的、可能是非凸的问题的最小化;
2)当 F ( x ) = ∣ ∣ A x − b ∣ ∣ 2 , G ( x ) = c ∣ ∣ x ∣ ∣ 1 F({\bf{x}})=||{\bf{Ax-b}}||^2, G({\bf{x}})=c||{\bf{x}}||_1 F(x)=∣∣Ax−b∣∣2,G(x)=c∣∣x∣∣1,其中 A 、 b 、 c {\bf{A}、b}、c A、b、c为给定的常数, X = R n , A ∈ R m × n X=R^n,{\bf{A}}\in R^{m \times n} X=Rn,A∈Rm×n,此时问题为著名的LASSO问题[2];
3)当 F ( x ) = ∣ ∣ A x − b ∣ ∣ 2 , G ( x ) = c ∑ i = 1 N ∣ ∣ x i ∣ ∣ 2 F({\bf{x}})=||{\bf{Ax-b}}||^2, G({\bf{x}})=c\sum\limits_{i=1}^N||{\bf{x}}_i||_2 F(x)=∣∣Ax−b∣∣2,G(x)=ci=1∑N∣∣xi∣∣2,其中 A 、 b 、 c {\bf{A}、b}、c A、b、c为给定的常数, X = R n , A ∈ R m × n X=R^n,{\bf{A}}\in R^{m \times n} X=Rn,A∈Rm×n,此时问题为group LASSO问题[3];
4)当 F ( x ) = ∑ j = 1 m l o g ( 1 + e − a j y j T x ) , G ( x ) = c ∣ ∣ x ∣ ∣ 1 ( o r G ( x ) = c ∑ i = 1 N ∣ ∣ x i ∣ ∣ 2 ) F({\bf{x}})=\sum\limits_{j=1}^mlog(1+e^{-a_j{\bf{y}}_j^T{\bf{x}}}), ~ G({\bf{x}})=c||{\bf{x}}||_1(or ~ G({\bf{x}})=c\sum\limits_{i=1}^N||{\bf{x}}_i||_2) F(x)=j=1∑mlog(1+e−ajyjTx), G(x)=c∣∣x∣∣1(or G(x)=ci=1∑N∣∣xi∣∣2),其中 y j 、 a j 、 c {\bf{y}_j}、a_j、c yj、aj、c为给定的常数,此时问题转换为稀疏逻辑回归问题(sparse logistic regression problem)[4-5];
5)当 F ( x ) = ∑ j = 1 m max { 0 , 1 − a j y j T x } , G ( x ) = c ∣ ∣ x ∣ ∣ 1 F({\bf{x}})=\sum\limits_{j=1}^m \max\{0,1-a_j{\bf{y}}_j^T{\bf{x}}\},G({\bf{x}})=c||{\bf{x}}||_1 F(x)=j=1∑mmax{0,1−ajyjTx},G(x)=c∣∣x∣∣1, 其中 a i ∈ { − 1 , 1 } a_i \in\{-1,1\} ai∈{−1,1}, y j 、 c {\bf{y}_j}、c yj、c给定,此时问题为 l 1 l_1 l1-regularized l 2 l_2 l2-loss SVM 问题(SVM:支持向量机)[6]。
[1]F. Facchinei, G. Scutari and S. Sagratella, “Parallel Selective Algorithms for Nonconvex Big Data Optimization,” in IEEE Transactions on Signal Processing, vol. 63, no. 7, pp. 1874-1889, April1, 2015, doi: 10.1109/TSP.2015.2399858.
[2]R. Tibshirani, “Regression shrinkage and selection via the lasso,” J. Roy. Statist. Soc. Series B (Methodol.), pp. 267–288, 1996.
[3] M. Yuan and Y. Lin, “Model selection and estimation in regression with grouped variables,” J. Roy. Statist. Soc. Series B (Statist. Methodol.), vol. 68, no. 1, pp. 49–67, 2006.
[4] S. K. Shevade and S. S. Keerthi, “A simple and efficient algorithm for gene selection using sparse logistic regression,” Bioinformatics, vol. 19, no. 17, pp. 2246–2253, 2003.
[5]L. Meier, S. Van De Geer, and P. Bühlmann, “The group lasso for logistic regression,” J. Roy. Statist. Soc. Series B (Statist. Methodol.), vol. 70, no. 1, pp. 53–71, 2008.
[6]G.-X. Yuan, K.-W. Chang, C.-J. Hsieh, and C.-J. Lin, “A comparison of optimization methods and software for large-scale l1-regularized linear classification,” J. Mach. Learn. Res., vol. 11, pp. 3183–3234, 2010.
- SCA方法解析[7]
该方法用于求解目标函数和约束均是非凸(non-convex)的问题,如下问题可采用SCA求解:
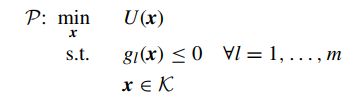
其中目标函数U为光滑(可能非凸)且 g l g_l gl也是光滑(可能非凸),主要思想是:对原函数进行凸逼近并且不断迭代,最终的原问题的解可以通过合适的凸逼近得到。原问题的替代函数如下所示:
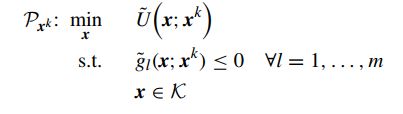
其中 U ~ ( x ; x k ) \tilde U(x;x^k) U~(x;xk)和 g ~ l ( x ; x k ) \tilde g_l(x;x^k) g~l(x;xk)是 U ( x ) , g l ( x ) U(x), ~g_l(x) U(x), gl(x)在第k次迭代的近似值。
1)假设在每次迭代时,一些原始函数 U ( x ) U(x) U(x)和 g l ( x ) g_l(x) gl(x)近似于它们的上界,但保留相同的一阶行为, 论文[7]中给出伪代码:

2)当目标函数U可以不是自己的上界,此时求解方式如下:
首先要假设如下关于 g ~ l \tilde g_l g~l的条件成立:
a. g ~ l ( ∗ , y ) \tilde g_l(*,y) g~l(∗,y)在定义域是凸函数
b.上界: g l ( x ) ≤ g ~ l ( x ; y ) g_l(x) \le \tilde g_l(x;y) gl(x)≤g~l(x;y)
c.函数值连续: g ~ l ( y ; y ) = g l ( y ) \tilde g_l(y;y)=g_l(y) g~l(y;y)=gl(y)
d. g ~ l ( ∗ ; ∗ ) \tilde g_l(*;*) g~l(∗;∗)连续
e. g ~ l ( ∗ ; ∗ ) \tilde g_l(*;*) g~l(∗;∗)的一阶导连续
f.梯度连续性: ∇ x g ~ l ( y ; y ) = ∇ x g l ( y ) {\nabla _x}{\tilde g_l}(y;y) = {\nabla _x}{g_l}(y) ∇xg~l(y;y)=∇xgl(y)
其次假设关于U的条件如下:
a… U ~ ( ∗ , y ) \tilde U(*,y) U~(∗,y)在定义域内保持强凸性,即给定常数 μ \mu μ,有
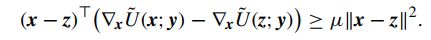
b.梯度连续性: ∇ x U ~ ( y ; y ) = ∇ x U ( y ) {\nabla _x}{\tilde U}(y;y) = {\nabla _x}{U}(y) ∇xU~(y;y)=∇xU(y)
c. ∇ x U ~ ( ∗ ; ∗ ) {\nabla _x}{\tilde U}(*;*) ∇xU~(∗;∗)连续
根据上述假设,有如下三种普遍情况:
(1) g l ( x ) g_l(x) gl(x)的近似: g l ( x ) g_l(x) gl(x)由两个凸函数之差组成(DC:difference of convex 结构),即 g l ( x ) = g l + ( x ) − g l − ( x ) g_l(x)=g_l^+(x)-g_l^-(x) gl(x)=gl+(x)−gl−(x), 此时得到 g l g_l gl的上界逼近:
![]()
(2) g l ( x ) g_l(x) gl(x)的近似: g l ( x ) g_l(x) gl(x)由函数乘积结构组成(PF:product of functions),即 g l ( x ) = f 1 ( x ) f 2 ( x ) g_l(x)=f_1(x)f_2(x) gl(x)=f1(x)f2(x), 且 f 1 和 f 2 f_1和f_2 f1和f2为凸函数且非负,此时可以转换成DC形式如下:
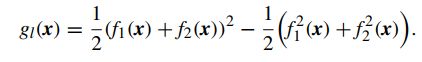
同DC,有其上界逼近为:
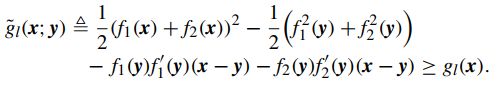
(3) U ( x ) U(x) U(x)的近似: 认为其有PF的结构,即 U ( x ) = h 1 ( x ) h 2 ( x ) U(x)=h_1(x)h_2(x) U(x)=h1(x)h2(x), 且 h 1 和 h 2 h_1和h_2 h1和h2为凸函数且非负, 此时其凸逼近有:

其中 τ > 0 , 且 H ( y ) \tau>0, 且{\bf{H(y)}} τ>0,且H(y)为正定矩阵。
[7]Yu Z , Gong Y , Gong S , et al. Joint Task Offloading and Resource Allocation in UAV-Enabled Mobile Edge Computing[J]. IEEE Internet of Things Journal, 2020, PP(99):1-1.
总结:SCA的方法首先应用于求解目标函数非凸和条件约束非凸的情况,其次SCA主要是通过迭代求解一系列与原问题相似的凸优化问题的解,当最终收敛条件成立时,此时得到的解便可以近似看成原问题的解。具体地,首先第k次迭代点的值为 y k y_k yk,利用上述形式对该点求其替代函数,此时,求解该替代函数(convex)的解,再利用第k次与第k+1次的值的关系得到 y k + 1 y_{k+1} yk+1,重复上述步骤,直到某条件收敛。
【以上均参考有关文献,并作出自己的理解,如有不对,还请指正,谢谢】