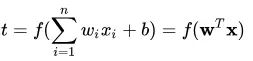BP(BackPropagation)神经网络算法详解
一、BP神经网络背景
BP(back propagation)神经网络是1986年由Rumelhart和McClelland为首的科学家提出的概念,是一种按照误差逆向传播算法训练的多层前馈神经网络,是应用最广泛的神经网络。
在人工神经网络的发展历史上,感知机(Multilayer Perceptron,MLP)网络曾对人工神经网络的发展发挥了极大的作用,但是,随着研究工作的深入,人们发现它还存在不足,例如无法处理非线性问题,从而限制了它的应用。增强网络的分类和识别能力、解决非线性问题的唯一途径是采用多层前馈网络,即在输入层和输出层之间加上隐含层。构成多层前馈感知器网络。

常见的神经网络所使用的是层级结构,每层神经元与下一神经元全互连,神经元之间不存在同层连接,也不存在跨层连接。这样的神经网络通常称为”多层前馈神经网络“(multi-layer feedforward neural networks)。其中输入层神经元接收外界输入,隐层与输出层神经元对信号进行加工,最终结果由输出层神经元输出;换言之,输入层神经元仅是接受输入,不进行函数处理,隐层与输出层包含功能神经元。神经网络的学习过程,就是根据训练数据来调整神经元之间的“连接权”以及每个功能神经元的阈值;换言之,神经网络“学”到的东西,蕴涵在连接权与阈值中.
示例神经网络输入层包含4个神经元,隐层包含6个神经元,输出层包含4个盛神经元
从结构上讲,BP网络具有输入层、隐藏层和输出层;从本质上讲,BP算法就是以网络误差平方为目标函数、采用梯度下降法来计算目标函数的最小值。
BP神经网络的训练过程包含3个阶段,首先是信号的前向传播阶段,然后是误差的反向传播阶段,最后是权值和阈值的更新阶段,如此反复迭代,在大于最大迭代次数或者小于目标误差时停止迭代,所得到的就是训练好的BP神经网络模型
知识补充–感知机
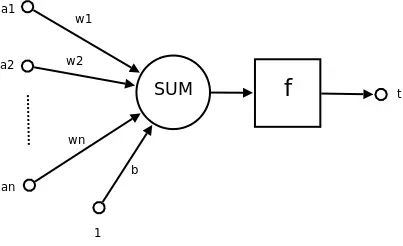
感知机(Perception)是神经网络和 SVM(支持向量机)的基础,是一种二分类的线性分类模型。为了形象地说明一下感知机的工作机理,可以用神经网络中的感知机模型来描述一下,下图是维基百科中描述感知机的模型图。
图中, n维向量[a1,a2,…,an]的转置作为感知机的输入,[w1,w2,…,wn]的转置为输入分量连接到感知机的权重(weifht),b 为偏置(bias),f(.)为激活函数,t 为感知机的输出。t 的数学表示为:
另外,这里的 f(.) 用的是符号函数:可以看出,符号函数是非连续的,不光滑的,这只是激活函数的一种
二、BP神经网络原理
给定训练集: D = { ( x 1 , y 1 ) , ( x 2 , y 2 ) , … , ( x m , y m ) } , x i ∈ R d , y i ∈ R l D=\{(x_1,y_1),(x_2,y_2),\ldots,(x_m,y_m)\},x_i\in\mathbb{R}^d,y_i\in\mathbb{R}^l D={(x1,y1),(x2,y2),…,(xm,ym)},xi∈Rd,yi∈Rl。即输入示例由d个属性描述,输出l维实值向量。在神经网络中,输入神经元与输出神经元的个数便由这两个值确定,即有d个输入神经元,l个输出神经元,而隐层的层数和所包含的神经元个数由实际问题确定,这里假设只有一层,包含q个隐层神经元。

接下来介绍两个概念,权值和阈值,上文曾说,神经网络训练出的东西,蕴藏在这两个值中,因此这两个概念极为重要。BP神经网络中不同层之间相互连接,信号在不同层之间的传递需要通过带权重的连接进行传递。阈值存在于隐层神经元和输出神经元之中,在本示例神经网络中,隐层神经元接收来自输入层的信号,隐层的每个神经元接收到的总输入值与神经元的阈值进行比较,然后通过“激活函数”处理以产生神经元的输出。输出层的神经元也是以同样方式产生神经元的输出。
为便于区分,输入层第i个神经元与隐层第h个神经元之间的连接权 v i h v_{ih} vih,隐层第h个神经元与输出层第j个神经元之间的连接权为 ω h j \omega_{hj} ωhj。隐层第h个神经元的阈值使用 γ h \gamma_h γh表示,输出层的第j个神经元的阈值使用 θ j \theta_j θj表示。
记隐层第h个神经元接收到的输入为 α h \alpha_h αh,输出为 b h b_h bh。输出层第j个神经元接收到的输入为 β j \beta_j βj
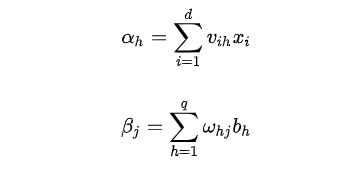
本示例中隐层与输出层的激活函数都采用Sigmoid函数。

对训练样例 ( x k , y k ) (x_k,y_k) (xk,yk) ,假定神经网络的输出为 y k ^ = ( y ^ 1 k , y ^ 2 k , … , y ^ l k ) \hat{y_k}=(\hat{y}_1^k,\hat{y}_2^k,\ldots,\hat{y}_l^k) yk^=(y^1k,y^2k,…,y^lk) ,即: y ^ j k = f ( β j − θ j ) \hat{y}_j^k=f(\beta_j-\theta_j) y^jk=f(βj−θj)。则网络在 ( x k , y k ) (x_k,y_k) (xk,yk)上的均方误差为: E k = 1 2 ∑ j = 1 l ( y ^ j k − y j k ) 2 E_k=\frac{1}{2}\sum_{j=1}^l(\hat{y}_j^k-y_j^k)^2 Ek=21j=1∑l(y^jk−yjk)2
权值的更新:BP神经网络基于梯度下降策略,以目标的负梯度方向对参数进行调整。
给定学习率 η \eta η,(学习率 η ∈ ( 0 , 1 ) \eta\in(0,1) η∈(0,1)由训练者自己给出,学习率控制着每一轮迭代的更新步长,若太大则容易振荡,若太小则收敛速度过慢。目前没有合适的办法计算最准确的学习率)。
输出层的梯度: g j = y ^ j k ( 1 − y ^ j k ) ( y j k − y ^ j k ) g_j=\hat{y}_j^k(1-\hat{y}_j^k)(y_j^k-\hat{y}_j^k) gj=y^jk(1−y^jk)(yjk−y^jk)
隐层的梯度: e h = b h ( 1 − b h ) ∑ j = 1 l ω h j g j e_h=b_h(1-b_h)\sum_{j=1}^l\omega_{hj}g_j eh=bh(1−bh)∑j=1lωhjgj
更新公式: Δ ω h j = η g j b h \Delta\omega_{hj}=\eta g_jb_h Δωhj=ηgjbh
Δ θ j = − η g j \Delta\theta_j=-\eta g_j Δθj=−ηgj
Δ v i h = η e h x i \Delta v_{ih}=\eta e_hx_i Δvih=ηehxi
Δ γ h = − η e h \Delta\gamma_h=-\eta e_h Δγh=−ηeh
单词迭代代码
import numpy as np
#输入
x=np.array([[1,0,1]]).T
#目的结果
y=np.array([[1]]).T
#初始权值和阈值
w1=np.array([[0.2,-0.3],
[0.4,0.1],
[-0.5,0.2]])
w2=np.array([[-0.3,-0.2]])
b=np.array([[-0.4,0.2,0.1]]).T
#参数
net_max_time=2000 #最大迭代次数
net_goal=0.00001 #目标误差
net_lr=0.9 #学习率
def sigmoid(num1,num2):
return 1/(1+np.exp(num2-num1))
m1,n1=np.shape(w1)
m2,n2=np.shape(w2)
m3,n3=np.shape(b)
#正向传播
v=[]
for i in range(n1):
v.append(sigmoid(w1[:,i].dot(x),b[i])) #输入层至隐含层
v.append(sigmoid(w2.dot(v),b[-1])) #隐含层至输出层
#反向计算梯度
gra=[]
gra.append(v[-1]*(1-v[-1])*(y-v[-1])) #输出层至隐含层
for j in range(n2)[::-1]:
gra.append(v[j]*(1-v[j])*gra[0]*w2[0][j])
gra.reverse() #矩阵反转
#更新权值
for i in range(m2):
for j in range(n2):
w2[i][j]=w2[i][j]+net_lr*v[j]*gra[-1]
for i in range(m1):
for j in range(n1):
w1[i][j]=w1[i][j]+net_lr*x[i]*gra[j]
#更新阈值
b[-1]=b[-1]-net_lr*gra[-1]
for i in range(m3-1):
b[i][0]=b[i][0]-net_lr*gra[i]
print("更新权值后的w(输入层至隐层):\n",w1)
print("更新权值后的w(隐层至输出层):\n",w2.T)
print("更新阈值后的b:\n",b)
三、参考
1、https://juejin.im/post/5e06d21ff265da33e056a181
2、《机器学习》
3、百度百科