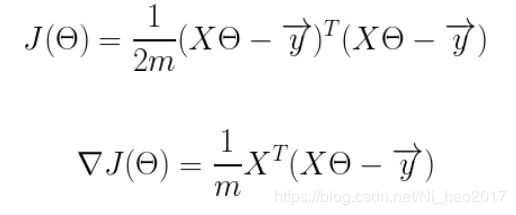numpy和pytorch实现梯度下降法
1 梯度下降原理
首先,我们有一个可微分的函数。这个函数就代表着一座山。我们的目标就是找到这个函数的最小值,也就是山底。根据之前的场景假设,最快的下山的方式就是找到当前位置最陡峭的方向,然后沿着此方向向下走,对应到函数中,就是找到给定点的梯度 ,然后朝着梯度相反的方向,就能让函数值下降的最快!
所以,我们重复利用这个方法,反复求取梯度,最后就能到达局部的最小值,这就类似于我们下山的过程。而求取梯度就确定了最陡峭的方向,也就是场景中测量方向的手段。
1.1 梯度
梯度就是分别对每个变量进行微分,然后用逗号分割开,梯度是用<>包括起来,说明梯度其实一个向量。
梯度是微积分中一个很重要的概念,梯度的意义:
在单变量的函数中,梯度其实就是函数的微分,代表着函数在某个给定点的切线的斜率;
在多变量函数中,梯度是一个向量,向量有方向,梯度的方向就指出了函数在给定点的上升最快的方向.
梯度的方向是函数在给定点上升最快的方向,那么梯度的反方向就是函数在给定点下降最快的方向,这正是我们所需要的。所以我们只要沿着梯度的方向一直走,就能走到局部的最低点!
1.2 梯度的数学解释

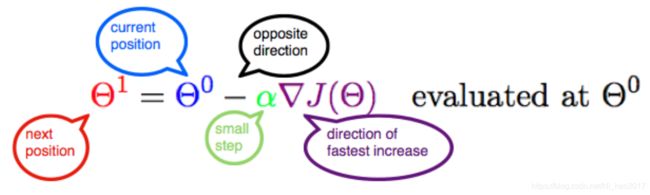
此公式的意义是:J是关于Θ的一个函数,我们当前所处的位置为Θ0点,要从这个点走到J的最小值点,也就是山底。首先我们先确定前进的方向,也就是梯度的反向,然后走一段距离的步长,也就是α,走完这个段步长,就到达了Θ1这个点!
2 梯度下降算法实现——线性回归模型
2.1 numpy
定义一个代价函数,在此我们选用均方误差代价函数
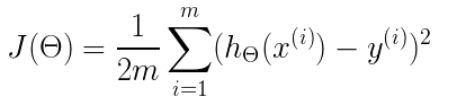
m是数据集中点的个数
½是一个常量,这样是为了在求梯度的时候,二次方乘下来就和这里的½抵消了,自然就没有多余的常数系数,方便后续的计算,同时对结果不会有影响
y 是数据集中每个点的真实y坐标的值
h 是我们的预测函数,根据每一个输入x,根据Θ 计算得到预测的y值,即
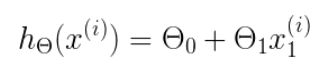
我们有两个变量,为了对这个公式进行矩阵化,我们可以给每一个点x增加一维,这一维的值固定为1,这一维将会乘到Θ0上。这样就方便我们统一矩阵化的计算
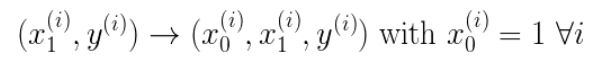
我们将代价函数和梯度转化为矩阵向量相乘的形式
2.1.1 定义数据集和学习率
import numpy as np
m = 20
# Points x-coordinate and dummy value (x0, x1).
#构建m行,1列的矩阵,矩阵值都为1
X0 = np.ones((m, 1))
#X1的值是1,到m+1间的随机数,转化为二维数组
X1 = np.arange(1, m+1).reshape(m, 1)
#np.hstack():在水平方向上平铺
X = np.hstack((X0, X1))
# Points y-coordinate
y = np.array([
3, 4, 5, 5, 2, 4, 7, 8, 11, 8, 12,
11, 13, 13, 16, 17, 18, 17, 19, 21
]).reshape(m, 1)
# The Learning Rate alpha.
alpha = 0.01
2.1.2 以矩阵向量的形式定义代价函数和代价函数的梯度
def error_function(theta, X, y):
'''Error function J definition.定义代价函数J'''
#np.dot计算矩阵的积
diff = np.dot(X, theta) - y
#返回对应计算结果
return (1./2*m) * np.dot(np.transpose(diff), diff)
def gradient_function(theta, X, y):
'''Gradient of the function J definition.梯度函数'''
diff = np.dot(X, theta) - y
return (1./m) * np.dot(np.transpose(X), diff)
2.1.3 算法的核心部分——梯度下降迭代计算¶
当梯度小于1e-5时,说明已经进入了比较平滑的状态,类似于山谷的状态,这时候再继续迭代效果也不大了,所以这个时候可以退出循环!
def gradient_descent(X, y, alpha):
'''Perform gradient descent.'''
#先定义初始theta值
theta = np.array([1, 1]).reshape(2, 1)
#根据给定的theta计算出梯度
gradient = gradient_function(theta, X, y)
#在梯度大于1e-5时进行迭代
while not np.all(np.absolute(gradient) <= 1e-5):
#根据梯度公式计算新的theta
theta = theta - alpha * gradient
#根据theta计算新的theta值
gradient = gradient_function(theta, X, y)
return theta
# 导入必要的包
import torch
from torch.autograd import Variable
import torch.nn as nn # 模型包,里面包含了各种各样的模型,方便我们直接使用
import matplotlib.pyplot as plt
import numpy as np
import torchsnooper
# 生成用来进行线性回归的模拟数据
X1 = torch.unsqueeze(torch.linspace(1, 21,20), dim = 1)
y = X1 + 0.8 * torch.rand(X1.size())
# 为了能够自动求导,我们要将 x, y 变成 Variable 对象
X = Variable(X1) # PyTorch中的 Variable 默认是允许自动求导的,所以 requires_grad=True 可以不加
Y = Variable(y) # 同上
定义函数
# 定义参数初始化函数
@torchsnooper.snoop()
def init_parameters():
W = Variable( torch.randn(1, 1), requires_grad=True) # 随机初始化 w,同theta
b = Variable( torch.zeros(1, 1), requires_grad=True ) # 初始化偏差
parameters = {"W": W, "b": b}
return parameters
# 定义模型
#这个函数是 y = w*X+b
@torchsnooper.snoop()
def model(X, parameters):
return X * parameters["W"] + parameters["b"]
# 定义损失函数
@torchsnooper.snoop()
def square_loss(y_hat, Y):
#loss = (y_hat - Y)的平方和,同函数J
loss = (y_hat - Y).pow(2).sum()
return loss
# 使用梯度来更新参数
@torchsnooper.snoop()
def update_parameters(parameters, lr):
#求解梯度值来更新参数,lr是学习速率(步长)
#该函数即为theta1 = theta0 - ...
parameters["W"].data -= lr * parameters["W"].grad.data
parameters["b"].data -= lr * parameters["b"].grad.data
return
#### 超参数 ####
EPOCH = 100 # 迭代次数
learning_rate = 0.001 # 学习速率
parameters = init_parameters() # 参数初始化
#### 开始训练 ####
for t in range(EPOCH):
# 对x进行预测
y_hat = model(X, parameters)
# 计算损失
loss = square_loss(y_hat, Y)
# 反向求导
loss.backward()
# 通过梯度,更新参数
update_parameters(parameters, learning_rate)
if (t+1) % 20 == 0:
print(loss)
# 因为自动求导会对梯度自动地积累,所以,我们要清除梯度
parameters["W"].grad.data.zero_()
parameters["b"].grad.data.zero_()
# 画图
plt.scatter(X.data.numpy(), Y.data.numpy())
plt.plot(X.data.numpy(), y_hat.data.numpy(), 'r-', lw = 4)
plt.show()
print("实际的参数w是: 5 \n" )
print("预测的参数w是", parameters["W"])
print("预测的常数项是:" , parameters["b"])
3 神经网络实现
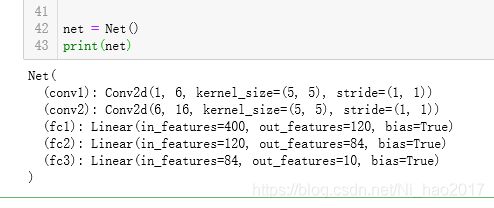
3.1 定义网络
import torch
import torch.nn as nn
import torch.nn.functional as F
class Net(nn.Module):
def __init__(self):
super(Net, self).__init__()
# 输入图像channel:1;输出channel:6;5x5卷积核
#卷积层'1’, 示输人图片力孕遏道,飞'表示输出心道坎 .'5'-I<.示春 积扛为 5•5
self.conv1 = nn.Conv2d(1, 6, 5)
#卷积层
self.conv2 = nn.Conv2d(6, 16, 5)
# an affine operation: y = Wx + b
#仿射层/全连接层
self.fc1 = nn.Linear(16 * 5 * 5, 120)
self.fc2 = nn.Linear(120, 84)
self.fc3 = nn.Linear(84, 10)
def forward(self, x):
# 2x2 Max pooling
#卷积->激活->池化
x = F.max_pool2d(F.relu(self.conv1(x)), (2, 2))
# 如果是方阵,则可以只使用一个数字进行定义
x = F.max_pool2d(F.relu(self.conv2(x)), 2)
#‘-1’表示自适应
x = x.view(-1, self.num_flat_features(x))
x = F.relu(self.fc1(x))
x = F.relu(self.fc2(x))
x = self.fc3(x)
return x
def num_flat_features(self, x):
size = x.size()[1:] # 除去批处理维度的其他所有维度
num_features = 1
for s in size:
num_features *= s
return num_features
3.2 损失函数
output = net(input)
target = torch.randn(10) # 本例子中使用模拟数据
target = target.view(1, -1) # 使目标值与数据值形状一致
criterion = nn.MSELoss()
loss = criterion(output, target)
print(loss)
3.3 反向传播
net.zero_grad() # 清零所有参数(parameter)的梯度缓存
print('conv1.bias.grad before backward')
print(net.conv1.bias.grad)
loss.backward()
print('conv1.bias.grad after backward')
print(net.conv1.bias.grad)
3.4 更新权重
learning_rate = 0.01
for f in net.parameters():
f.data.sub_(f.grad.data * learning_rate)
import torch.optim as optim
# 创建优化器(optimizer)
optimizer = optim.SGD(net.parameters(), lr=0.01)
# 在训练的迭代中:
optimizer.zero_grad() # 清零梯度缓存
output = net(input)
loss = criterion(output, target)
loss.backward()
optimizer.step() # 更新参数
4.参考资料
- https://www.jianshu.com/p/c7e642877b0e
- https://pytorch.apachecn.org/docs/1.0/blitz_neural_networks_tutorial.html