2020杭电多校第五场

Tetrahedron

本场签到题,直角四面体的三个直角边长在[1~n]中随机生成,设直角顶点到地面的距离为h,问 1/h^2的期望是多少.

简单推一推就知道$$h=\frac{abc}{\sqrt{a^2{b}^2+b^2{c}^2+a^2{c}^2}}$$
所以
$$\frac{1}{h^2}=\frac{1}{a^2}+\frac{1}{b^2}+\frac{1}{c^2}$$

所以我们只需要知道a,b,c出现了几次就好了,很容易就可以推出1,2,3,4…n的出现概率是相同的,所以每个数字出现的次数就是3n^2 (一共有n^3种可能,每种可能有3位数字一共有3n^3个数字,由n种数字均分)
最后再除以总情况数n^3就得到了
$$ans=\frac{3\ast {\sum }_{i=1}^n\frac{1}{i^2}}{n}$$

这个题会卡nlogn,求逆元的时候要用O(n)的方法
ACcode:

#include 
#include 
#define MAX 6000060
#define ll long long
using namespace std;

ll k[MAX];
const int mod=998244353;
ll inv[MAX];
int invinit(){
    inv[1]=1;
    for(int i=2;i<MAX;++i){
        inv[i]=(mod-mod/i)*1ll*inv[mod%i]%mod;
    }
}

void init()
{
    for(int i=1;i<MAX;i++)
        k[i]=(inv[i]*inv[i])%mod;
    for(int i=1;i<MAX;i++)
        k[i]=(k[i-1]+k[i])%mod;
    for(int i=1;i<MAX;i++)
        k[i]=(k[i]*3)%mod;
}


int main()
{
    invinit();
    init();
    int t;
    scanf("%d",&t);
    while(t--)
    {
        int a;
        scanf("%d",&a);
        printf("%lld\n",(k[a]*inv[a])%mod);
    }
    
    return 0;
}

Paperfolding

还是一个概率题,理论上比A难,但比赛的时候这个题比A先过…
通过简单的画图就可以发现最后剪开的线是连续的,

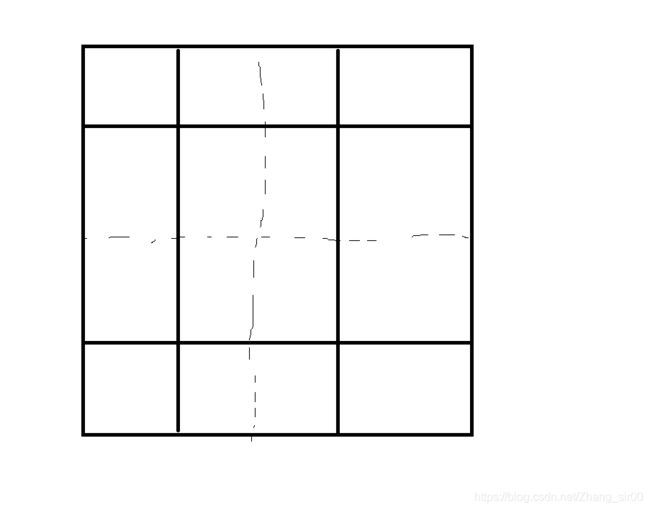
上图黑色实线就是剪开的地方虚线是折痕,可以发现,最后的形状是一个网格,只要知道了行数和列数,就不难得到纸片的个数,同时观察发现设f(n)为沿一方向折n次最后网格的列(行)数为:
$$f(n)=2^n+1$$
设一共折n次所有情况的和为G(n),则G(n)为:
$$G(n)=\sum _{i=1}^{n}C(n,i)\ast f(i)\ast f(n-i)$$
其中
$$f(i)\ast f(n-i)=2^n+2^i+2^{n-i}+1$$

故原式可化简为:
$$\begin{gathered} G(n)=2^n\ast (2^n+1)+\sum _{i=1}^{n}C(n,i)(2^i+2^{n-i}) \\ =2^n\ast (2^n+1)+2\ast 3^n \end{gathered}$$

ACcode:

#include 
#include 
#define ll long long
#define mod 998244353
using namespace std;

ll mul(ll a,ll b)
{
    ll ans=1;
    while(b)
    {
        if(b&1) ans=(ans*a)%mod;
        b>>=1;
        a=(a*a)%mod;
    }
    return ans;
}

ll getinv(ll x)
{
    return mul(x,mod-2);
}
int main()
{
    int t;
    scanf("%d",&t);
    while(t--)
    {
        ll n;
        scanf("%lld",&n);
        ll k_2=mul(2,n);
        ll inv=getinv(k_2);
        ll k_3=(2*mul(3,n))%mod;
        ll ans=((((k_2+1)*k_2)%mod+k_3)%mod)*inv;
        printf("%lld\n",ans%mod);
    }
    
    return 0;
}

Set1

打表的胜利!!!

通过打表求出每个数字有多少种情况被剩下:
打表代码:

#include 
#include 
#include 
#include 
#define MAX 100
using namespace std;
vector<int> k;

int cas[MAX];

void dfs(int t)
{
	if(t==0)
	cas[k[0]]++;
	int begin=k[0];
	k.erase(k.begin());
	for(int i=0;i<k.size();i++)
	{
		int now=k[i];
		k.erase(k.begin()+i);
		dfs(t-1);
		k.push_back(now);
		sort(k.begin(),k.end());
	}
	k.push_back(begin);
	sort(k.begin(),k.end());
}


int main()
{
	int n;
	scanf("%d",&n);
	for(int i=1;i<=n;i++)
	{
		k.push_back(i);
	}
	
	dfs(n/2);
	for(int i=1;i<=n;i++)
	cout<<cas[i]<<endl;
	return 0;
}

下面是带有前导零的结果

可以发现有n/2个前导零.

下面是省略前导零的结果:

沿着这些线不难发现规律,我们只需要做些预处理(阶乘&斜线上的值),我们就可以O(1)的找到每个位置上的值,总体复杂度O(n)
ACcode:

#include 
#include 
#define MAX 5000050
#define ll long long
#define mod 998244353
using namespace std;

ll pre[MAX*2];
ll last[MAX*2];

ll ans[MAX];


ll mul(ll a,ll b)
{
    ll ans=1;
    while(b)
    {
        if(b&1) ans=(ans*a)%mod;
        b>>=1;
        a=(a*a)%mod;
    }
    return ans;
}

ll getinv(ll x)
{
    return mul(x,mod-2);
}
void init()
{
    pre[0]=1;
    last[1]=1;
    for(int i=1;i<MAX;i++)
        pre[i]=(pre[i-1]*i)%mod;
    for(int i=2;i<MAX;i++)
        last[i]=(last[i-1]*(2*i-3))%mod;
}


int main()
{
    init();
    int t;
    scanf("%d",&t);
    while(t--)
    {
        int n;
        scanf("%d",&n);
        n=(n/2)+1;
        ll sum=0;
        for(int i=1;i<n;i++)
        {
            ans[i]=(last[i]*(pre[n+i-2]*getinv(pre[2*i-2])%mod))%mod;
            sum=(ans[i]+sum)%mod;
//            cout<
        }
//        cout<
        ans[n]=last[n];
        sum=(sum+last[n])%mod;
        for(int i=1;i<n;i++)
        printf("0 ");
        ll inv=getinv(sum);
        for(int i=1;i<=n;i++)
        {
            printf("%lld",ans[i]*inv%mod);
            if(i!=n)
            printf(" ");
        }
        printf("\n");
    }
    
    return 0;
}

Boring Game

队友过了…明天再说吧…