数学建模--相关性分析及Python实现

写在前面：
笔记为自行整理，内容出自课程《数学建模学习交流》，主讲人：清风

---

相关系数只是用来衡量两个变量线性相关程度的指标，因此，使用相关系数衡量相关性前需要确认变量间是线性相关的。

相关系数

import pandas as pd
import numpy as np
import matplotlib.pyplot as plt

%matplotlib inline

# 支持显示中文
plt.rcParams['font.family'] = ['sans-serif']
plt.rcParams['font.sans-serif'] = ['SimHei']
plt.rcParams['axes.unicode_minus']=False

data = pd.read_excel('eighth_girl.xlsx')

data.head()

	身高	体重	肺活量	50米跑	立定跳远	坐位体前屈
0	155	51	1687	9.7	158	9.3
1	158	52	1868	9.3	162	9.6
2	160	59	1958	9.9	178	9.5
3	163	59	1756	9.7	183	10.1
4	165	60	1575	9.0	156	10.4

data.info()

RangeIndex: 591 entries, 0 to 590
Data columns (total 6 columns):
身高       591 non-null int64
体重       591 non-null int64
肺活量      591 non-null int64
50米跑     591 non-null float64
立定跳远     591 non-null int64
坐位体前屈    591 non-null float64
dtypes: float64(2), int64(4)
memory usage: 27.8 KB

统计信息

dsc = data.describe()
dsc

	身高	体重	肺活量	50米跑	立定跳远	坐位体前屈
count	591.000000	591.000000	591.000000	591.000000	591.000000	591.000000
mean	156.003384	46.783418	2333.233503	10.792014	166.825719	9.496616
std	7.389410	5.031473	350.436154	1.310873	16.813587	2.938186
min	135.000000	16.000000	1450.000000	7.800000	52.000000	0.500000
25%	151.000000	44.000000	2109.000000	9.800000	156.000000	7.800000
50%	157.000000	47.000000	2391.000000	10.700000	167.000000	9.600000
75%	161.000000	50.000000	2570.000000	11.500000	178.000000	11.600000
max	171.000000	65.000000	3272.000000	15.000000	205.000000	17.500000

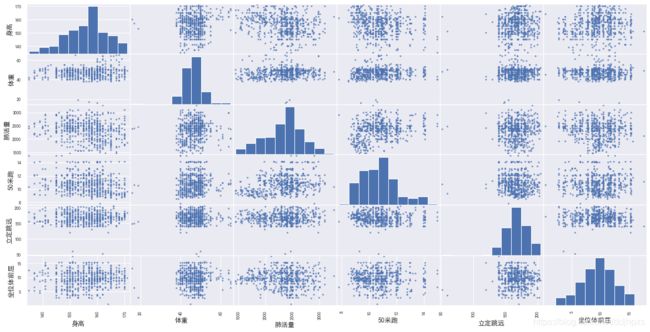
相关系数矩阵图

pd.plotting.scatter_matrix(data, figsize=(20,10), alpha=0.75)
plt.show()

相关系数矩阵

cor = data.corr()  # 默认method='pearson'
cor

	身高	体重	肺活量	50米跑	立定跳远	坐位体前屈
身高	1.0000	0.0665	-0.2177	-0.1920	0.0440	0.0951
体重	0.0665	1.0000	0.0954	0.0685	0.0279	-0.0161
肺活量	-0.2177	0.0954	1.0000	0.2898	0.0248	-0.0749
50米跑	-0.1920	0.0685	0.2898	1.0000	-0.0587	-0.0019
立定跳远	0.0440	0.0279	0.0248	-0.0587	1.0000	-0.0174
坐位体前屈	0.0951	-0.0161	-0.0749	-0.0019	-0.0174	1.0000

import seaborn as sns
sns.set(font='SimHei')  # 支持中文显示

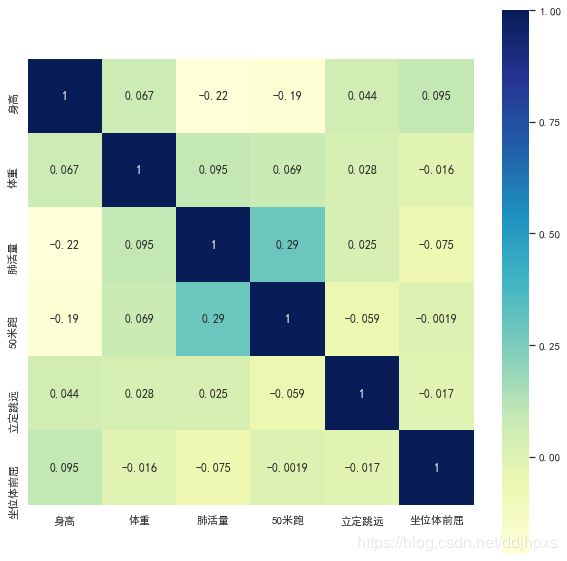
可视化矩阵

fig, ax = plt.subplots(figsize = (10,10))

# cor：相关系数矩阵
# cmap：颜色
# xticklabels：显示x轴标签
# yticklabels：显示y轴标签
# annot：方块中显示数据
# square：方块为正方形

sns.heatmap(cor, cmap='YlGnBu', xticklabels=True, yticklabels=True,
            annot=True, square=True)

相关系数的假设检验

第一步：提出原假设和$H_0$和备择假设$H_1$；假设已得到一个皮尔逊相关系数$r$，要想检验它是否显著的异于0，可以设定：$H_0：r=0，H_1：r\ne 0$
第二步：在原假设成立的条件下，利用要检验的量构造出一个符合某一分布的统计量。对于皮尔逊相关系数$r$而言，可以构造统计量：
$$t=r\sqrt{\frac{n-2}{1-r^2}}$$
可以证明，$t$是服从自由度为$n-2$的$t$分布。
第三步：将要检验的值带入这个统计量中，可以得到一个特性的值。假设计算出的相关系数为0.5，样本为30，则可以得到$t^{\ast }=0.5\sqrt{\frac{30-2}{1-0.5^2}}=3.05505$
第四步：根据$t$分布的定义可以得到置信水平为0.95的$t$分布的置信区间。做比较即可。

from scipy import stats
np.set_printoptions(suppress=True)  # 不使用用科学计数法
pd.set_option('display.float_format',lambda x : '%.4f' % x)  # 保留小数点后4位有效数字

# 0.975分位数
tp = stats.t.isf(1-0.975, 28)

x = np.linspace(-5,5,100)
y = stats.t.pdf(x, 28)
plt.plot(x,y)
plt.vlines(-tp, 0, stats.t.pdf(-tp, 28), colors='orange')
plt.vlines(tp, 0, stats.t.pdf(tp, 28), colors='orange')
plt.fill_between(x, 0, y, where=abs(x)>tp, interpolate=True, color='r')

更简便的方法：求p值

# 自定义求解p值矩阵的函数
def my_pvalue_pearson(x):
    col = x.shape[1]
    col_name = x.columns.values
    p_val = []
    for i in range(col):
        for j in range(col):
            p_val.append(stats.pearsonr(x[col_name[i]], x[col_name[j]])[1])
    p_val = pd.DataFrame(np.array(p_val).reshape(col, col), columns=col_name, index=col_name)
    p_val.to_csv('p_val_pearson.csv')  # 此处实则为多此一举，目的是借助带有excel格式的数据使得输出更美观
    p_val = pd.read_csv('p_val_pearson.csv', index_col=0)
    return p_val

my_pvalue_pearson(data)

	身高	体重	肺活量	50米跑	立定跳远	坐位体前屈
身高	0.0000	0.1061	0.0000	0.0000	0.2859	0.0208
体重	0.1061	0.0000	0.0204	0.0960	0.4978	0.6963
肺活量	0.0000	0.0204	0.0000	0.0000	0.5469	0.0687
50米跑	0.0000	0.0960	0.0000	0.0000	0.1542	0.9637
立定跳远	0.2859	0.4978	0.5469	0.1542	0.0000	0.6728
坐位体前屈	0.0208	0.6963	0.0687	0.9637	0.6728	0.0000

将p值与0.05做比较即可

正态分布检验

Jarque-Bera检验（n>30)

x = stats.norm.rvs(2, 3, 100)    
skewness = stats.skew(x)  # 偏度
kurtosis = stats.kurtosis(x)  # 峰度
jbtext = stats.jarque_bera(x)
print('偏度为：',skewness)
print('峰度为：',kurtosis)
print('J-B值：',jbtext[0])
print('p-value:',jbtext[1])

偏度为： 0.05657245566213502
峰度为： -0.135509867406316
J-B值： 0.1298528963460595
p-value: 0.9371363889360985

def my_jbtext(x):
    col_name = x.columns.values
    col_cnt = x.shape[1]
    h_mat = np.zeros(col_cnt)
    p_mat = np.zeros(col_cnt)
    for i in range(col_cnt):
        p_val = stats.jarque_bera(data[col_name[i]])[1]
        p_mat[i] = p_val
        if p_val >= 0.05:
            h_mat[i] = 0  # 通过原假设
        else:
            h_mat[i] = 1  # 拒绝原假设
    print(h_mat)
    print(p_mat)  # 各列的p值

my_jbtext(data)

[1. 1. 1. 1. 1. 1.]
[0.00602083 0.         0.00853    0.         0.         0.03949912]

1代表拒绝原假设，0代表接受

Shapiro-wilk检验(3<=n<=50)

stats.shapiro(data['身高'])  # 单个变量

(0.9839125275611877, 4.196843292447738e-06)

def my_shaptext(x):
    col_name = x.columns.values
    col_cnt = x.shape[1]
    h_mat = np.zeros(col_cnt)
    p_mat = np.zeros(col_cnt)
    for i in range(col_cnt):
        p_val = stats.shapiro(data[col_name[i]])[1]
        p_mat[i] = p_val
        if p_val >= 0.05:
            h_mat[i] = 0  # 通过原假设
        else:
            h_mat[i] = 1  # 拒绝原假设
    print(h_mat)
    print(p_mat)  # 各列的p值

my_shaptext(data)

[1. 1. 1. 1. 1. 1.]
[0.0000042  0.         0.00000207 0.         0.         0.00005767]

Q-Q图（大样本时使用）

stats.probplot(data['身高'], dist="norm", plot=plt)
plt.show()

斯皮尔曼相关系数

定义：$X$和$Y$为两组数据，其斯皮尔曼相关系数：
$$r_s=1-\frac{6{\sum }_{i=1}^n{d}_i^2}{n\left(n^2-1\right)}$$
其中，$d_i$为$X_i$和$Y_i$之间的等级差。（一个数的等级是指，将其所在的一列数按照从小到大的顺序排列后，这个数作在的位置；若有相同的数值，则他们的等级为所在位置的算数平均）
可以证明：$r_s$位于$-1$和$1$之间。

data.corr(method='spearman')

	身高	体重	肺活量	50米跑	立定跳远	坐位体前屈
身高	1.0000	0.0301	-0.2430	-0.1990	0.0624	0.1099
体重	0.0301	1.0000	0.1305	0.0898	0.0216	-0.0488
肺活量	-0.2430	0.1305	1.0000	0.2626	0.0219	-0.0801
50米跑	-0.1990	0.0898	0.2626	1.0000	-0.0910	-0.0029
立定跳远	0.0624	0.0216	0.0219	-0.0910	1.0000	-0.0399
坐位体前屈	0.1099	-0.0488	-0.0801	-0.0029	-0.0399	1.0000

斯皮尔曼相关系数的假设检验

# 自定义求解p值矩阵的函数
def my_pvalue_spearman(x):
    col = x.shape[1]
    col_name = x.columns.values
    p_val = []
    for i in range(col):
        for j in range(col):
            p_val.append(stats.spearmanr(x[col_name[i]], x[col_name[j]])[1])
    p_val = pd.DataFrame(np.array(p_val).reshape(col, col), columns=col_name, index=col_name)
    p_val.to_csv('p_val_spearman.csv')  # 此处实则为多此一举，目的是借助带有excel格式的数据使得输出更美观
    p_val = pd.read_csv('p_val_spearman.csv', index_col=0)
    return p_val

my_pvalue_spearman(data)

	身高	体重	肺活量	50米跑	立定跳远	坐位体前屈
身高	0.0000	0.4647	0.0000	0.0000	0.1295	0.0075
体重	0.4647	0.0000	0.0015	0.0290	0.5996	0.2362
肺活量	0.0000	0.0015	0.0000	0.0000	0.5944	0.0517
50米跑	0.0000	0.0290	0.0000	0.0000	0.0270	0.9436
立定跳远	0.1295	0.5996	0.5944	0.0270	0.0000	0.3330
坐位体前屈	0.0075	0.2362	0.0517	0.9436	0.3330	0.0000

斯皮尔曼相关系数和皮尔逊相关系数的选择：

1.连续数据，正态分布，线性关系，用pearson相关系数是最恰当，当然用spearman相关系数也可以， 就是效率没有pearson相关系数高。
2.上述任一条件不满足，就用spearman相关系数，不能用pearson相关系数。
3.两个定序数据之间也用spearman相关系数，不能用pearson相关系数。
定序数据是指仅仅反映观测对象等级、顺序关系的数据，是由定序尺度计量形成的，表现为类别，可以进行排序，属于品质数据。
例如：优、良、差；
我们可以用1表示差、 2表示良、 3表示优，但请注意，用2除以1得出的2并不
代表任何含义。定序数据最重要的意义代表了一组数据中的某种逻辑顺序。
注：斯皮尔曼相关系数的适用条件比皮尔逊相关系数要广，只要数据满足单调关系
（例如线性函数、指数函数、对数函数等）就能够使用。