算法题04：分治法：求第K小元素（线性时间选择算法）

求第k小元素

题目内容：

给定一个线性序列集，要求使用分治法求出其中指定的第 $K$ 小的数的值和位置，如给定 $n$ 个元素和一个整数 $i$，$1\le i\le n$，输出这 $n$ 个元素中第 $i$ 小元素的值及其位置。

一、问题分析（模型、算法设计和正确性证明等）

解决第K小问题有如下几种方法

①将n个数排序(比如快速排序或归并排序)，选取排序后的第k个数，时间复杂度为$O(nlogn)$。

②维护一个k个元素的最大堆，存储当前遇到的最小的k个数，时间复杂度为$O(nlogk)$。这种方法同样适用于海量数据的处理。

③部分的快速排序（快速选择算法），每次划分之后判断第k个数在左右哪个部分，然后递归对应的部分，平均时间复杂度为$$O(n)$$。但最坏情况下复杂度为$O(n^2)$。

④线性时间选择算法，修改快速选择算法的主元选取规则，使用中位数的中位数的作为主元，最坏情况下时间复杂度为$O(n)$。

​ 实验要求使用分治策略，所以可以使用归并排序、快速排序、以及线性时间选择算法，我选择的是线性时间选择算法，本质上是快速排序的升级版，算法的思想是修改快速选择算法的主元选取方法，提高算法在最坏情况下的时间复杂度。

​ 算法的思路是：

1. 首先把数组按5个数为一组进行分组，最后不足5个的忽略。对每组数进行排序（如插入排序）求取其中位数。
2. 把上一步的所有中位数移到数组的前面，对这些中位数递归调用线性时间选择算法求得他们的中位数。
3. 将上一步得到的中位数作为划分的主元进行整个数组的划分。
4. 判断第k个数在划分结果的左边、右边还是恰好是划分结果本身，前两者递归处理，后者直接返回答案。

二、复杂度分析

​ 当$n<75$时，时间复杂度很低，近似于常数, n大于75时，划分时以5个元素为一组求取中位数，共得到n/5个中位数，再递归求取中位数，复杂度为T(n/5)，剩余要处理的最大规模变为$3n/4$，加上多次线性扫描，其时间复杂度为$C_{2}n$，所以可以得到递推式：

$\begin{array}{rl}T(n)& \le \{\begin{array}{ll}{C}_1& n<75\\ C_{2}n+T(n/5)+T(3n/4)& n\ge 75\end{array}\\ \therefore T(n)=O(n)& \end{array}$

三、程序实现和测试过程和结果（主要描述出现的问题和解决方法）

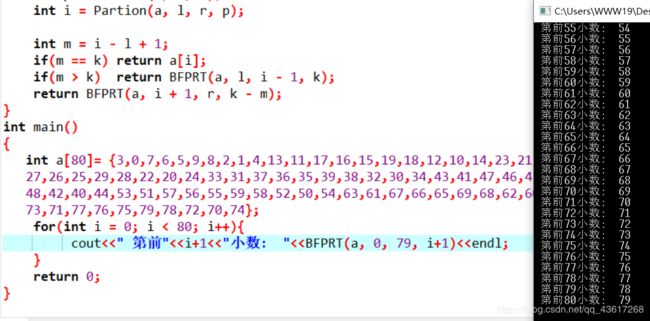
伪代码：

public static int DAC_Linear_Select(int a[], int l, int r, int key)
{
    if(a.length <= 5):		//当长度小于5时，直接使用冒泡排序，返回查找到的值
    	bubbleSort(a,l,r);
    	return a[key-1];
    
    int index=l-1; 		//定义中位数替换下标
    for(int star=l,end; (end=star+4)<=r; st+=5){
        bubbleSort(a,star,end);//每五个数排序
        swap(a,++t,star+2);	   //将中位数替换到数组前面，便于递归求取中位数的中位数
    }
    
    int pivot=DAC_Linear_Select(a, l, l+(r-l-4)/5, (l+(r+l-4)/5-l+1)/2);
    int i =  partition(a, l, r, pivotId), j = i-l+1;
    if(key==j) return a[j];		//相等则直接返回
    else if(key<j) return DAC_Linear_Select(a,l,j-1,key); 	//小于则向左递归
    else return DAC_Linear_Select(a, j+1,r,key-j)			//大于则向右递归
}

java代码：

package root;

/**
 * @author 宇智波Akali
 * 这是线性时间选择算法(BFPRT算法)解决前k小问题程序
 * @version2.0
 */
public class T3_DAC_Liner_SelectN {
	
	public static void swap(int a[], int i,int j){
		int temp=a[j];
		a[j] = a[i];
		a[i] = temp;
	}
	//冒泡排序
	public static void bubbleSort(int a[], int l, int r){
	    for(int i=l; i<r; i++)
			{
				for(int j=i+1; j<=r; j++)
				{
					if(a[j]<a[i])swap(a,i,j);
				}
			}
	}
	//递归寻找中位数的中位数
	public static int FindMid(int a[], int l, int r){
	    if(l == r) return l;
	    int i = 0;
	    int n = 0;
	    for(i = l; i < r - 5; i += 5)
	    {
	        bubbleSort(a, i, i + 4);
	        n = i - l;
	        swap(a,l+n/5, i+2);
	    }
	  //处理剩余元素
	    int num = r - i + 1;
	    if(num > 0)
	    {
	        bubbleSort(a, i, i + num - 1);
	        n = i - l;
	        swap(a,l+n/5, i+num/2);
	    }
	    n /= 5;
	    if(n == l) return l;
	    return FindMid(a, l, l + n);
	}
	//进行划分过程
	public static int Partion(int a[], int l, int r, int p){
	    swap(a,p, l);
	    int i = l;
	    int j = r;
	    int pivot = a[l];
	    while(i < j)
	    {
	        while(a[j] >= pivot && i < j)
	            j--;
	        a[i] = a[j];
	        while(a[i] <= pivot && i < j)
	            i++;
	        a[j] = a[i];
	    }
	    a[i] = pivot;
	    return i;
	}
	 
	public static int Select(int a[], int l, int r, int k){
	    int p = FindMid(a, l, r);    //寻找中位数的中位数
	    int i = Partion(a, l, r, p);
	 
	    int m = i - l + 1;
	    if(m == k) return a[i];
	    if(m > k)  return Select(a, l, i - 1, k);
	    return Select(a, i + 1, r, k - m);
	}
	public static void main(String[] args) {
		int a[]= {3,0,7,6,5,9,8,2,1,4,13,11,17,16,15,19,18,12,10,14,23,21,
				   27,26,25,29,28,22,20,24,33,31,37,36,35,39,38,32,30,34,43,41,47,46,45,49,
				   48,42,40,44,53,51,57,56,55,59,58,52,50,54,63,61,67,66,65,69,68,62,60,64,
				   73,71,77,76,75,79,78,72,70,74};
		for(int i = 0; i < 80; i++){
			System.out.println("第"+(i+1)+"小数为： "+Select(a, 0, 79, i+1));
		}
	}
}

​ 算法的思路倒是容易理解，但是把算法转换为代码就有太多细节要处理，不同编程语言之间也有差异，一开始用Java写的，结果因为参数传递的机制没注意，数组值交换有bug,java中定义swap(a[],i,j),要把数组也传进去。

运行结果：

我输入的数组为10个随机数，循环输出低k小数，结果如下：

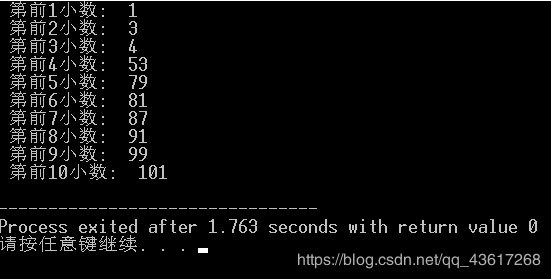
为了确保正确性，我又测试了长度为80的0-79的乱序数组，结果也正确。