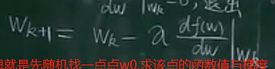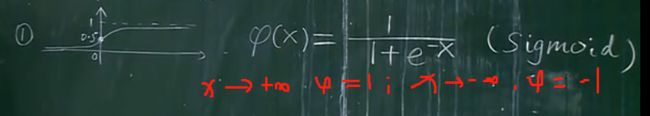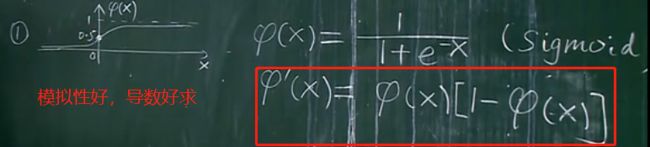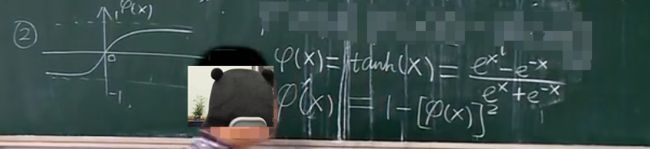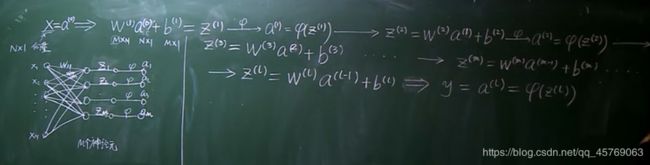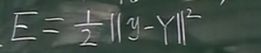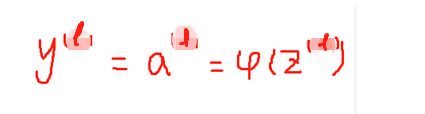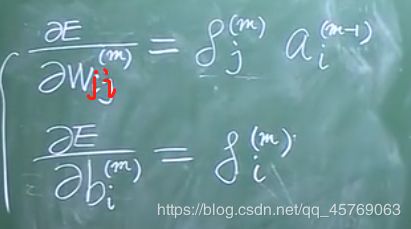机器学习——人工神经网络之后向传播算法(BP算法)
目录
一、后向传播算法的本质——梯度下降法求局部极值
1、w迭代公式的合理性
二、后向传播算法的推导(以二层神经网络为例)
1、问题描述(创建目标函数loss函数,求参数)
2、求解参数的流程(四步曲)
3、求解参数第二步——目标函数对每一个参数求偏导(BP算法目的所在)
>>>问题1:为什么叫做后向传播算法(BP)?
>>>问题2:非线性函数fai的改造(重要)——激活函数
1)fai的改造函数形式一
2)fai的改造函数形式二
3)fai的改造函数形式三
4)fai的改造函数形式四
三、多层神经网络的向量模型以及BP算法求参(w(m)、b(m))流程步骤
1、多层神经(l层)网络的向量模型(前向传播流程)
1)关于多层神经网络向量模型中的一些定义
2)多层神经(l层)网络的向量模型
>>>问题3:上图中w(m),b(m)是怎么变化的?
2、BP算法(后向传播算法)流程
1)推导利用BP求偏导(链式法则)——已知第m+1层求第m层
2)所有对参数w,b的偏导
3)求解所有w,b参数小结(求解流程)
>>>问题4:w,b迭代公式中的α怎么进行取值?
一、后向传播算法的本质——梯度下降法求局部极值
这里需要注意的是区分SVM和BP,SVM找的是全局的最优解,BP寻找的是局部的最优解
1、w迭代公式的合理性
w的迭代公式是为了让函数值一直减小,直到在局部达到最小,即导数为0,那迭代公式能否完成极值点的寻找呢?证明如下:
从上图可知,通过w的迭代公式,可以让函数值随w的迭代而一直减小,直到找到极值点
二、后向传播算法的推导(以二层神经网络为例)
1、问题描述(创建目标函数loss函数,求参数)
下面为二层神经网络,有9个未知参数,目的是在让E函数值最小的情况下求解这9个参数
2、求解参数的流程(四步曲)
3、求解参数第二步——目标函数对每一个参数求偏导(BP算法核心)
第二步结束,执行第三步和第四步,直到满足条件时所有的参数w,b就算出来了
>>>问题1:为什么叫做后向传播算法(BP)?
答:如下图所示,
我们首先要从前往后通过输入的X来计算,a和z、y的表达式(前向计算),
然后再从后到前依次计算对各个参数的偏导,因此BP算法的目的就是用来求目标函数对参数的偏导的,所以叫后向传播算法
>>>问题2:非线性函数fai的改造(重要)——激活函数
求目标函数对参数求偏导时含有fai的导数,而前面说fai是阶跃函数,那其导数恒等于0,在0处无穷大,那该怎么把fai的导数带入到求参数偏导的式子中去呢?
答:这样的fai函数肯定是不行的,为此对fai函数进行了改造,改造成了以下几种形式
建议先看文章:《机器学习——人工神经网络之多层神经网络(多层与三层)——数学模型中的非线性函数fai》
用以下的fai函数和三层神经网络模型结合也可以解决所有的线性问题
1)fai的改造函数形式一
2)fai的改造函数形式二
以下两种是深度学习常被用到的fai函数
3)fai的改造函数形式三
4)fai的改造函数形式四
三、多层神经网络的向量模型以及BP算法求参(w(m)、b(m))流程步骤
1、多层神经(l层)网络的向量模型(前向传播流程)
1)关于多层神经网络向量模型中的一些定义
2)多层神经(l层)网络的向量模型
>>>问题3:上图中w(m),b(m)是怎么变化的?
答:w(m)和b(m)是待求参数,上图只是通过数学的推导来表示清楚多层神经网络模型中各个参数的变化以及关系式,至于怎么求w(m)和b(m)依旧使用的是BP算法,具体怎么求看后面部分
2、BP算法(后向传播算法)流程
注意:
1、这里得区分开y和Y的关系,y是变量,Y是输入的标签是已知量,但是两者的维度是一致的
2、链式法则指的就是求复合函数的偏导的法则
1)推导利用BP求偏导(链式法则)——已知第m+1层求第m层
①链式1:最后一层(l层)的偏导
②链式2:第m层的偏导——从后往前推的递推式
2)所有对参数w,b的偏导
通过下面四个式子可以将目标函数对所有参数的偏导求解出来
3)求解所有w,b参数小结(求解流程)
1、任意取一组参数w,b,
2、求出目标函数对所有参数w,b的偏导的表达式
3、将w,b的值代入偏导公式求出偏导值
4、根据w,b的迭代公式对w,b参数进行更新,得到新的一组w,b参数
5、若目标函数对所有的参数的偏导为0,则取该组w,b参数作为最优模型的参数,否则一直进行循环,直到偏导都为0
通过上述就将模型确定了
>>>问题4:w,b迭代公式中的α怎么进行取值?
答:α在模型中叫做步长,这个参数的取值,一般是通过调整得到的,过大可能会导致错过最好的参数,过小收敛效率慢。总的来说这个参数的取值随缘,先定一个步长,算出w,b后,再慢慢调节阿尔法的值
对模型中的参数该怎么进行设置呢?请看文章:《机器学习——人工神经网络之参数设置(BP算法)》