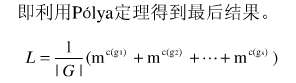2013 Multi-University Training Contest 4

1001 Palindrome subsequence

版刷题我们又没过，还能说什么呢。。。太弱了，区间DP，队友思路对了，不过写挫了，少加个条件。。各种WA，TLE。我一直用组合数学方法做的，各种无法实现。赛后才发现很简单的，直接dp[i][j]表示回文串的数量，然后递推。

#include
#include
#include
#include
#include
#include
#include
using namespace std;
inline void RD(int &ret)
{
    char c;
    do
    {
        c=getchar();
    }
    while(c<'0'||c>'9');
    ret=c-'0';
    while((c=getchar())>='0'&&c<='9')
    {
        ret=ret*10+(c-'0');
    }
}
inline void OT(int a)
{
    if(a>=10)
    {
        OT(a/10);
    }
    putchar(a%10+'0');
}
int dp[1001][1001];
int main()
{
    int t,i,j,l,m,n,cas=0;
    char a[1001];
    RD(t);
    while(t--)
    {
        cas++;
        scanf("%s",a);
        l=strlen(a);
        memset(dp,0,sizeof(dp));
        for(i=0; i

1007 Group

树状数组维护，离线区间询问。

#include
#include
#include
#include
#include
#include
#include
using namespace std;
int n,c[100001];
int a[100001],b[100001],ac[100001];
inline void RD(int &ret)
{
    char c;
    do
    {
        c=getchar();
    }
    while(c<'0'||c>'9');
    ret=c-'0';
    while((c=getchar())>='0'&&c<='9')
    {
        ret=ret*10+(c-'0');
    }
}
inline void OT(int a)
{
    if(a>=10)
    {
        OT(a/10);
    }
    putchar(a%10+'0');
}
int lowbit(int x)
{
    return x&(-x);
}
int add(int n)
{
    int sum=0;
    while(n>0)
    {
        sum+=c[n];
        n-=lowbit(n);
    }
    return sum;
}
void updata(int i,int x)
{
    while(i<=n)
    {
        c[i]+=x;
        i+=lowbit(i);
    }
}
struct xl
{
    int lw,hi,id;
} s[100001];
bool cmp(xl x,xl y)
{
    return x.hi1&&b[a[i]-1]

1008 Hehe

恶搞题，也是本场的签到题，就是让你求出字符串中，“hehe”出现的次数，涉及到排列组合和斐波那契数列。

#include
#include
#include
#include
#include
#include
#include
using namespace std;
inline void RD(int &ret)
{
    char c;
    do
    {
        c=getchar();
    }
    while(c<'0'||c>'9');
    ret=c-'0';
    while((c=getchar())>='0'&&c<='9')
    {
        ret=ret*10+(c-'0');
    }
}
inline void OT(int a)
{
    if(a>=10)
    {
        OT(a/10);
    }
    putchar(a%10+'0');
}
int fc[10001];
void f()
{
    int i;
    fc[0]=1;
    fc[1]=1;
    fc[2]=2;
    for(i=3;i<10001;++i)
    {
        fc[i]=(fc[i-1]+fc[i-2])%10007;
    }
}
int main()
{
    int t,i,l,cas=0,sum,ans;
    f();
    RD(t);
    char a[10088];
    while(t--)
    {
        cas++;
        scanf("%s",a);
        l=strlen(a);
        sum=0;
        ans=1;
        for(i=0;i

1011 Fliping game

水博弈，可我还是想了很久，多亏学长提醒，只要考虑右下角点的初始状态就行了，‘0’为Bob，‘1’为Alice。

#include
#include
#include
#include
#include
#include
#include
using namespace std;
inline void RD(int &ret)
{
    char c;
    do
    {
        c=getchar();
    }
    while(c<'0'||c>'9');
    ret=c-'0';
    while((c=getchar())>='0'&&c<='9')
    {
        ret=ret*10+(c-'0');
    }
}
inline void OT(int a)
{
    if(a>=10)
    {
        OT(a/10);
    }
    putchar(a%10+'0');
}
int main()
{
    int t,i,j,a[111][111],m,n;
    RD(t);
    while(t--)
    {
        RD(n);
        RD(m);
        for(i=1;i<=n;++i)
        {
            for(j=1;j<=m;++j)
            {
                RD(a[i][j]);
            }
        }
        if(a[n][m]==0)
        {
            printf("Bob\n");
        }
        else
        {
            printf("Alice\n");
        }
    }
    return 0;
}

1002 Who's Aunt Zhang

这题是一道组合数学题，里面涉及到了我从来没接触到的Polya定理，不知道的可以百度一下。我也是看了这篇文章才明白一点皮毛的：传送门

标程上只给了一个公式，一个快速幂取模运算。

m=(p(n,74)+9*p(n,38)+8*p(n,26)+6*p(n,20));

这就是公式，我花了2,3个小时才明白了这里面所包含的深意。。。

由于是组合数学论，这里必须要用到，魔方置换群的知识，寻找循环节点，然后再套用公式。

这里的L是最终解，G代表状态总数，m是要涂的颜色种类，c(gi)是各个状态的循环节数。

由于是魔方是一个三维立体的物件，所以它的小正方形，节点，棱都是属于不同的状态。

小正方形：54个   节点：8个   棱：12条   

现在就要开始旋转寻找置换群和循环节点了：

旋转角度：

0度：由于没动，所以所有状态都算作自己的循环节：54个小面+8个节点+12条棱=74（由于没动，所以不存在向哪方面转的问题）；

90度：由于转动前后的位置不变，所以只有前后、左右、顺时针逆时针3种方式，而循环节的话，转动四次才会回归原来状态，所以总数有：(3*2(俩侧面)+9(转动轮面)+1*2(八条侧棱)+1(4条转动面棱)+1*2(两边的各四个点))=20；

180度：180度转动方式不太能想到，是由3种普通的前后、左右、顺时针逆时针和以6种对棱互换旋转组成，而循环节的话：普通：(5*2(俩侧面)+9*2(转动轮面)+2*2(八条侧棱)+2(4条转动面棱)+2*2(两边的各四个点))=38  对棱：(9(俩底面)+9*2(四个侧面)+1(对棱)+1*4(四条底面边长棱)+1*2(对棱点)+1*2(侧棱点)+2(位置不变的侧棱))=38

所以180度旋转的循环节数不变为38；

270度：由于和旋转90度相同，而且旋转方式为3种，循环节为20，所以90度和270度可以合并；

120度：这是最难想的一种旋转方式，由于有8个点的存在，所以绕着体对称轴旋转120度，旋转方式为4种，而循环节：(9*2(旋转轴上下各3个面)+1*2(上下与俩顶点相交的棱)+1*2(其它侧棱)+1*2(上下两个顶点)+1*2(上下旋转的各三个点))=26；

240度：与120度相同，旋转方式为4种

所以综上所述：

L=(m^74(旋转方式为1种)+(3+6)*m^38(普通旋转方式3种+对棱旋转方式6种)+(4+4)*m^26(120度和240度体对称轴的8种旋转方式)+(3+3)*m^20(90度和270度共6种旋转方式))/(1+3+6+4+4+3+3)

纯属自己YY，如果不对请批评指正。

#include
#include
#include
#include
#include
#include
using namespace std;
inline void RD(int &ret)
{
    char c;
    do
    {
        c=getchar();
    }
    while(c<'0'||c>'9');
    ret=c-'0';
    while((c=getchar())>='0'&&c<='9')
    {
        ret=ret*10+(c-'0');
    }
}
inline void OT(int a)
{
    if(a>=10)
    {
        OT(a/10);
    }
    putchar(a%10+'0');
}
__int64 p(__int64 x,__int64 y)//快速幂取模
{
    __int64 res=1;
    while(y>0)
    {
        if(y%2==1)
        {
            res=(res*x)%240168;
        }
        x=(x*x)%240168;
        y/=2;
    }
    return res%240168;
}
int main()
{
    int t,cas=0;
    __int64 n,m;
    RD(t);
    while(t--)
    {
        cas++;
        scanf("%I64d",&n);
        m=(p(n,74)+9*p(n,38)+8*p(n,26)+6*p(n,20))%240168;
        m=m/24;
        printf("Case %d: %I64d\n",cas,m);
    }
    return 0;
}

数论实在是太神了，我已经被搞爆了。。。