约瑟夫问题及变形:poj 1012
约瑟夫问题是个有名的问题:N个人围成一圈,从第一个开始报数,第M个将被杀掉,最后剩下一个,其余人都将被杀掉。例如N=6,M=5,被杀掉的顺序是:5,4,6,2,3,1。
给定N个人和m,计算最后获救者的编号,求解的思路是一种递推思想。
我们知道第一个人(编号一定是(m-1) mod n) 出列之后,剩下的n-1个人组成了一个新的约瑟夫环(以编号为k=m mod n的人开始):
k k+1 k+2 … n-2,n-1,0,1,2,… k-2,并且从k开始报0。
我们把他们的编号做一下转换:
k –> 0
k+1 –> 1
k+2 –> 2
…
…
k-2 –> n-2
变换后就完完全全成为了(n-1)个人报数的子问题,假如我们知道这个子问题的解:例如x是最终的胜利者,那么根据上面这个表把这个x变回去不刚好就是n个人情况的解吗?!!变回去的公式很简单,相信大家都可以推出来:x’=(x+k) mod n
如何知道(n-1)个人报数的问题的解?对,只要知道(n-2)个人的解就行了。(n-2)个人的解呢?当然是先求(n-3)的情况 —- 这显然就是一个倒推问题!好了,思路出来了,下面写递推公式:
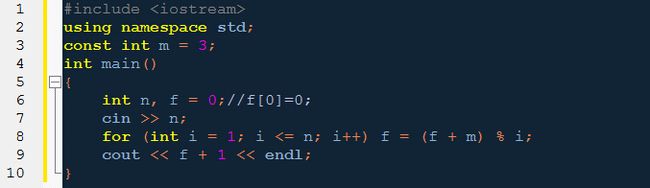
令f表示i个人玩游戏报m退出最后胜利者的编号,最后的结果自然是f[n]
递推公式
f[1]=0;
f=(f+m) mod i; (i>1)
有了这个公式,我们要做的就是从1-n顺序算出f的数值,最后结果是f[n]。因为实际生活中编号总是从1开始,我们输出f[n]+1
由于是逐级递推,不需要保存每个f,程序也是异常简单:
约瑟夫环变形 先引入Joseph递推公式,设有n个人(0,…,n-1),数m,则第i轮出局的人为
f(i)=(f(i-1)+m-1)%(n-i+1);
f(0)=0;
f(i) 表示当前子序列中要退出的那个人(当前序列编号为0~(n-i));
拿个例子说:K=4,M=30;
f(0)=0;
f(1)=(f(0)+30-1)%8=5; 序列(0,1,2,3,4,5,6,7)中的5
f(2)=(f(1)+30-1)%7=6; 序列(0,1,2,3,4,6,7)中的7
f(3)=(f(2)+30-1)%6=5; 序列(0,1,2,3,4,6)中的6
f(4)=(f(3)+30-1)%5=4; 序列(0,1,2,3,4)中的4
……..
依据题意,前K个退出的人必定是后K个人,所以只要前k轮中只要有一次f(i)小于k则此m不符合题意。
参考文章:
- ζёСяêτ - 小優YoU
http://blog.csdn.net/lyy289065406/article/details/6648444
书山有路,学海无涯
http://www.cnblogs.com/yu-chao/archive/2011/05/29/2062276.html
百度百科
http://baike.baidu.com/link?url=6uSi0WGzW2m4jOUpLJJ_GusbojECXU0DZQV1utfQSdQ9hpqJxPwAt1EWjU4iepdrVJt7m2nnqdqPFaJUvax0K_#3
根据这样的思路,求解poj 1012就很容易了。
![]()
先打表预处理,把每一个k的结果存储在Joseph[k]中,输出,避免超时。
参考代码+部分注释:
#include false;break;}//不满足条件就标记
}
if(ok) break;
m++;
}
Joseph[k]=m;
}
}
int main()
{
// freopen("input.txt","r",stdin);
init();
while(cin>>k&&k){
cout<return 0;
}



