Java 堆排序
堆排序
- 1、关于堆
- 2、调整堆
- 3、建最大堆
- 4、堆排序
1、关于堆
堆就是一个简单的数组。只是我们用一种完全二叉树的角度来看它。以最大堆为例,比如说我们有一棵如下的二叉树:
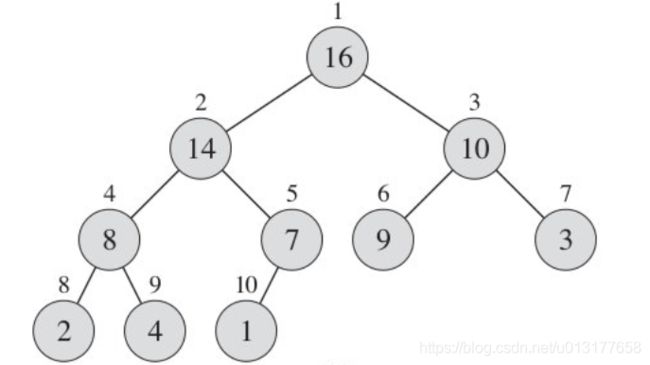
上图中,如果从根结点开始按照从左到右一层一层的编号的话,对这些元素的访问就构成了一个序列。比如上图中的序列按照编号顺序如下:16, 14, 10, 8, 7, 9, 3, 2, 4, 1
如果我们将这种从二叉树的结点关系转换成对应的数组形式的话,则对应的数组如下图:

从二叉树的每个结点的编码到它的左右字结点的关系,我们发现一个有意思的地方:
- 左子结点的编号 = 父结点编号 * 2
- 右子结点的编号 = 父结点编号 * 2 + 1
按照数组标的编号,有类似的对应关系:
- 左子结点的数组索引号 = 父结点索引号 * 2
- 右子结点的数组索引号 = 父结点索引号 * 2 + 1
在实现的时候考虑到我们的数组下标是从0开始的,对应的关系修改为:
- left(n) = n * 2 + 1
- right(n) = n * 2 + 2
对应的代码实现如下:
public static int left(int i) {
return i * 2 + 1;
}
public static int right(int i) {
return i * 2 + 2;
}
2、调整堆
前面我们已经理解了堆和对应的数组之间的关系了。
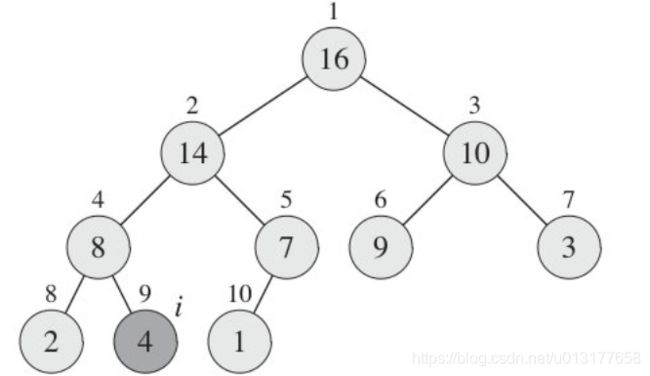
我们假定是要建立一个最大堆。它有一个重要的特性就是处于父结点的值必须比它的子结点要大。如果某一棵树上面的父结点不满足这个要求,我们就必须进行调整。笼统的说,调整就是将这个不符合条件的结点和子结点进行比较,通过交换将最大的结点作为父结点。具体的流程见下图:

在上图中,我们发现值为4的结点不符合要求。那么就需要进行交换调整。接着就需要在它的两个子结点中选择最大的那个,然后交换位置。它的子结点中最大的是14.交换之后的结果如下图:

经过交换之后,我们发现原来元素所在的位置确实符合要求了。可是4交换到新的结点之后又不符合最大堆的条件了。没办法,还需要继续选择最大子结点进行交换。这么一交换之后的结果如下:
经过这么两轮交换,我们终于可以保证以i = 2这个结点为根的树最终达到了一个符合最大堆的状态。总结前面这么一个交换调整的过程,主要如下:
- 比较当前结点和它的子结点,如果当前结点小于它的任何一个子结点,则和最大的那个子结点交换。否则,当前过程结束。
- 在交换到新位置的结点重复步骤1,直到叶结点。
对上面的过程进行细化之后编码,我们可以得到两个版本的方法:
- 递归版本
public static void maxHeapify(int[] a, int i) {
int l = left(i);
int r = right(i);
int largest = i;
if(l < a.length && a[l] > a[i])
largest = l;
if(r < a.length && a[r] > a[largest])
largest = r;
if(i != largest)
{
swap(a, i, largest);
maxHeapify(a, largest);
}
}
- 非递归版本
public static void maxHeapify(int[] a, int i)
{
int l = left(i);
int r = right(i);
int largest = i;
while(true)
{
if(l < a.length && a[l] > a[i])
largest = l;
if(r < a.length && a[r] > a[largest])
largest = r;
if(i != largest)
swap(a, i, largest);
else
break;
i = largest;
l = left(largest);
r = right(largest);
}
}
以上两个版本的实现主要有几个要点要注意:
- 每次求一个结点的子结点的时候要检查是否越界。
- 每次通过将当前结点和子结点的比较来选取最大值,如果最大值就是当前结点,则程序返回。
- 里面的swap方法就是交换两个索引位置元素的位置。
3、建最大堆
前面的过程主要针对的是一个树中的一个结点。如果树中间有多个结点不符合最大堆的条件,只调整某一个结点是没有用的。那么,就需要一个办法来将整棵树调整成符合条件的最大堆。
一个最简单的办法就是从最低层的结点开始起调整。很明显,如果我们从a[a.length -1]这样的结点来调整的话,有相当一部分结点是没必要的。因为这些结点很显然是叶结点,也就是说他们根本就没有子结点,连找子结点和去比较的必要都没有了。所以,我们可以从最后面往前到过来去找那些有子结点的结点,然后从这些结点开始一个个的进行堆调整。
首先第一个问题,从哪个结点开始进行调整。我们来看这棵二叉树,很显然,它最后的一个元素也肯定就是最终的一个叶结点。那么取它的父结点应该就是有子结点的最大号的元素了。那么从它开始就是最合适的。取它的父结点可以通过一个简单的i / 2来得到,i为当前结点的下标。
然后我们再来看第二个问题,为什么要从后往前而不是从前往后。这个相对也比较好理解。我们从下面的层开始调整,保证当上面的父结点来调整的时候,下面的子树已经满足最大堆的条件了。这样出现不符合条件的父结点只需要用前面的maxheapify过程就可以。而从前面往后调整呢,我们看下面的一个示例:

如果我们从根结点开始,根结点元素4比它的两个子结点都大,不需要调整。而再往后面的时候它的子结点1调整之后被换成16.这样就出现了它的子结点比它还要大的情况,因此从前往后这么调整的过程不行。
经过前面的讨论,构建最大堆的过程就相当的简单了:
public static void buildMaxHeap(int[] a) {
for(int i = a.length / 2; i >= 0; i--)
maxHeapify(a, i);
}
总的来说,建立最大堆的过程无非就是要建立一个符合如下条件的二叉树:它所有的结点值都比它的子结点要大。
4、堆排序
我通过建了一个最大堆,能够保证最大的元素就是根结点,那么,我们如果要从小到大排序的话,最大的元素就只要取根结点就可以了。如果我们把根结点拿走了,放到结果集的最末一个元素,接着就应该找第二大的元素。因为要保证这棵树本身是近似完全二叉树的性质,我们不能把中间的结点直接挪到根结点来比较。但是前面的maxHeapify过程提醒我们,如果我们从集合的最低一层叶结点来取,然后放到根结点进行调整的话,肯定也是可以得到剩下元素里面的最大结点的。就这样,我们可以得到这么一个过程:
- 取最大堆的根结点元素。
- 取集合最末尾的元素,放到根结点,调用maxHeapify进行调整。重复步骤1.
在具体实现的时候我们可以发现,每次都要取集合中后面的元素,我们原来得到的最大结点正好可以放到集合的末尾,正好达到最大的元素放到最后的效果。
public static void heapSort(int[] a) {
if(a == null || a.length <= 1)
return;
buildMaxHeap(a);
int length = a.length;
for(int i = a.length - 1; i > 0; i--) {
swap(a, i, 0);
length--;
maxHeapify(a, 0, length);
}
}
仔细看前面的代码,大家可能会发现一个细小的改变。就是maxHeapify方法多了个参数。这是因为考虑到实际情况下,如果每次我们把找到的当前集合最大元素放到后面了,那么这些元素就相当于从前面的集合中排除出来,后面进行堆调整的时候就不需要再考虑。所以用一个length的长度来限制调整的范围,以免伤及无辜:)。