Keras #1 - 训练一个小神经网络,并将它移植到单片机上运行
本文介绍了如何使用Keras框架,搭建一个小型的神经网络-多层感知器,并通过给定数据进行计算训练,最后将训练得到的模型提取出参数,在51单片机上进行部署运行。
目录
0 - 楔子
1 - 训练模型
1-1 模型的设计
1-2 数据集
1-3 模型的训练
1-4 模型的保存与再载入
2 - 部署模型
2-1 模型参数的提取
2-2 矩阵的运算方式
2-3 NNLayer
2-4 在单片机上运行
0 - 楔子
在前一篇文章(Keras #0 - 搭建Keras环境,跑一个例程),介绍了如何使用 Anaconda Navigator 进行方便快捷的 Keras 安装与部署,并且运行了一个例程来进行验证。
当逐渐熟悉Keras框架后,便想来自己设计一个神经网络,不需要太复杂,主要目的是为了让自己熟悉一下流程。了解一下制作一个神经网络需要准备一些相关的数据集,设计神经网络的结构,设计每一层的激活函数,设计最后进行模型训练时所需要用到的损失函数(loss)以及优化器(optimizer)等等。当然,如果能将训练好的模型运用到实际的部署环境中,而不是单纯的在PC上使用python进行运行,那便更好,于是便产生了这一篇的设计。
为了熟悉过程以及方便之后在单片机上尝试部署,我们这里的模型应当尽量简单,并且逻辑不复杂,方便我们去寻找或者直接产生训练所需要的数据集。
1 - 训练模型
1-1 模型的设计
我们设计一个网络,让它能够进行如下的简单运算:
这里,输入向量为一维,只含有三个元素 ![]() ,而输出则直接是该计算式的结果。例如当输入是
,而输出则直接是该计算式的结果。例如当输入是 ![]() 时,输出结果应当为 0.1 。
时,输出结果应当为 0.1 。
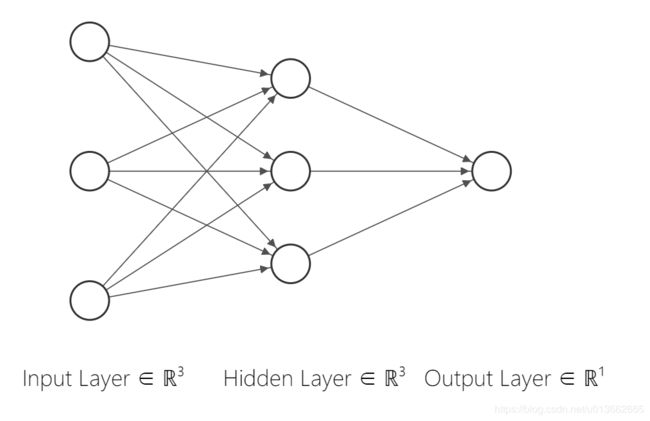
从分析的角度来看,这里的网络设计,只需要一层输入层,一层隐藏层还有一层输出层即可。其中隐藏层有3个神经元,输出层有一个神经元,使用 NN-SVG 绘制一下示意图:
是一个非常简单的神经网络模型,这种也被称之为 “多层感知机(MLP,Multi Layer Perceptron)”
那么,我们也可以根据设计,在 Keras中编写好该网络模型。由于输出是线性的,而不是进行分类操作,因此这里层与层之间的激活函数使用的是线性函数:
# 构建网络
model = Sequential()
model.add(Dense(3, activation='linear', input_shape=(3,)))
model.add(Dense(1, activation='linear'))1-2 数据集
为了训练我们的模型,数据是必不可少的。由于我们的神经网络是为了对一个特定计算式进行拟合,因此相应的训练与测试数据我们可以在程序中使用代码直接生成:
gTrainDataSize = 2000
gTestDataSize = 50
x_train = np.random.uniform(0, 1, size=(gTrainDataSize, 3))
y_train = np.zeros(shape=gTrainDataSize)
x_test = np.random.uniform(0, 1, size=(gTestDataSize, 3))
y_test = np.zeros(shape=gTestDataSize)
def GetTrainData():
np.random.seed(7)
print("正在产生训练数据")
for _index in range(x_train.shape[0]):
y_train[_index] = (x_train[_index, 0] * 0.1
+ x_train[_index, 1] * 0.2
+ x_train[_index, 2] * 0.3) / 2
# print("x_train:", x_train[_index, :])
print("x_train:", x_train)
print("y_train:", y_train)
print("训练数据产生完毕")
print("正在产生测试数据")
for _index in range(x_test.shape[0]):
y_test[_index] = (x_test[_index, 0] * 0.1
+ x_test[_index, 1] * 0.2
+ x_test[_index, 2] * 0.3) / 2
print("x_test:", x_test)
print("y_test:", y_test)
print("测试数据产生完毕")
通过修改 gTrainDataSize 与 gTestDataSize 来修改训练数据与测试数据的数量。 x_train 与 y_train 中分别存储的是训练输入与标准输出,用于进行训练。而 x_test 与 y_test 则是测试时所需的数据对。
在Keras的模型训练过程中,测试数据并不参与模型的训练,仅仅在模型训练的一个批次(BatchSize)训练完成后,丢入模型,比较输出的差(loss)与准确度(acc)来展示给用户方便评估。
1-3 模型的训练
接下来,可以开始模型的训练了,这里我将全代码贴出,方便查阅:
from __future__ import print_function
import keras
from keras.models import Sequential
from keras.layers import Dense
from keras.optimizers import SGD, RMSprop
from keras.utils import plot_model
import numpy as np
import matplotlib.pyplot as plt
# 超参数
gTrainDataSize = 2000
gTestDataSize = 50
gBatchSize = 20 # 整个训练数据分为多少批次进行训练
gEpochs = 10 # 整个训练数据将被重复训练的次数
'''
gSGD_lr = 0.01 # 这里不使用SGD作为优化器,使用默认参数的RMSprop来进行优化
gSGD_decay = 1e-6
gSGD_momentum = 0.01
'''
x_train = np.random.uniform(0, 1, size=(gTrainDataSize, 3))
y_train = np.zeros(shape=gTrainDataSize)
x_test = np.random.uniform(0, 1, size=(gTestDataSize, 3))
y_test = np.zeros(shape=gTestDataSize)
def GetTrainData():
np.random.seed(7)
print("正在产生训练数据")
for _index in range(x_train.shape[0]):
y_train[_index] = (x_train[_index, 0] * 0.1
+ x_train[_index, 1] * 0.2
+ x_train[_index, 2] * 0.3) / 2
# print("x_train:", x_train[_index, :])
print("x_train:", x_train)
print("y_train:", y_train)
print("训练数据产生完毕")
print("正在产生测试数据")
for _index in range(x_test.shape[0]):
y_test[_index] = (x_test[_index, 0] * 0.1
+ x_test[_index, 1] * 0.2
+ x_test[_index, 2] * 0.3) / 2
print("x_test:", x_test)
print("y_test:", y_test)
print("测试数据产生完毕")
def TrainModel():
# 获取训练与测试数据
GetTrainData()
# 构建网络
model = Sequential()
model.add(Dense(3, activation='linear', input_shape=(3,)))
model.add(Dense(1, activation='linear'))
# 输出各层参数情况
model.summary()
# 编译
'''
sgd = SGD(lr=gSGD_lr, decay=gSGD_decay, momentum=gSGD_momentum, nesterov=True)
model.compile(loss='mean_absolute_error', optimizer=sgd, metrics=['accuracy'])
'''
model.compile(loss='mean_absolute_error', optimizer=RMSprop(), metrics=['accuracy'])
# 训练
history = model.fit(x_train, y_train,
batch_size=gBatchSize,
epochs=gEpochs,
verbose=1,
validation_data=(x_test, y_test))
# 样本测试
ex_test = [0.2, 0.3, 0.4]
ex_val = (ex_test[0] * 0.1 + ex_test[1] * 0.2 + ex_test[2] * 0.3) / 2
exResult = model.predict(np.array([ex_test]))
print("-------\n模型输出结果为:", exResult)
print("计算结果为:", ex_val)
# 输出训练好的网络模型可视化
plot_model(model, to_file='myCalculatorModel.png')
# 训练历史可视化 绘制训练 & 验证的准确率值
'''
acc会一直是0,因为acc的计算是看模型输出结果与标准输出是否匹配,
而这里在计算过程中,很难’恰好‘碰到模型输出结果与标准输出匹配的时候,
故acc一般都一直是0,这里没有必要显示
'''
# plt.plot(history.history['acc'])
# plt.plot(history.history['val_acc'])
# plt.title('Model accuracy')
# plt.ylabel('Accuracy')
# plt.xlabel('Epoch')
# plt.legend(['Train', 'Test'], loc='upper left')
# plt.show()
# 绘制训练 & 验证的损失值
plt.plot(history.history['loss'])
plt.plot(history.history['val_loss'])
plt.title('Model loss')
plt.ylabel('Loss')
plt.xlabel('Epoch')
plt.legend(['Train', 'Test'], loc='upper left')
plt.show()
# 保存模型
print("Saving model to disk \n")
model.save("MyCalculatorModel.h5")
def LoadModelAndTest():
model = keras.models.load_model("./MyCalculatorModel.h5")
# 样本测试
ex_test = [0.2, 0.3, 0.4]
ex_val = (ex_test[0] * 0.1 + ex_test[1] * 0.2 + ex_test[2] * 0.3) / 2
exResult = model.predict(np.array([ex_test]))
print("-------\n模型输出结果为:", exResult)
print("计算结果为:", ex_val)
if __name__ == '__main__':
LoadModelAndTest()
# TrainModel()这里模型使用的损失函数是平均绝对误差(mean_absolute_error),优化器(optimizer)则使用了Keras提供了默认参数的RMSprop,代码中也注释了如何使用随机梯度下降(Stochastic Gradient Descent)来作为优化器的代码。
在模型训练的时候,需要提供几个参数:批(Batch),轮次(Epoch)。这两个参数的意义可以参考 Keras 官方文档中的介绍("sample", "batch", "epoch" 分别是什么?)
为了正确地使用 Keras,以下是必须了解和理解的一些常见定义:
- Sample: 样本,数据集中的一个元素,一条数据。
- 例1: 在卷积神经网络中,一张图像是一个样本。
- 例2: 在语音识别模型中,一段音频是一个样本。
- Batch: 批,含有 N 个样本的集合。每一个 batch 的样本都是独立并行处理的。在训练时,一个 batch 的结果只会用来更新一次模型。
- 一个 batch 的样本通常比单个输入更接近于总体输入数据的分布,batch 越大就越近似。然而,每个 batch 将花费更长的时间来处理,并且仍然只更新模型一次。在推理(评估/预测)时,建议条件允许的情况下选择一个尽可能大的 batch,(因为较大的 batch 通常评估/预测的速度会更快)。
- Epoch: 轮次,通常被定义为 「在整个数据集上的一轮迭代」,用于训练的不同的阶段,这有利于记录和定期评估。
- 当在 Keras 模型的
fit方法中使用validation_data或validation_split时,评估将在每个 epoch 结束时运行。- 在 Keras 中,可以添加专门的用于在 epoch 结束时运行的 callbacks 回调。例如学习率变化和模型检查点(保存)。
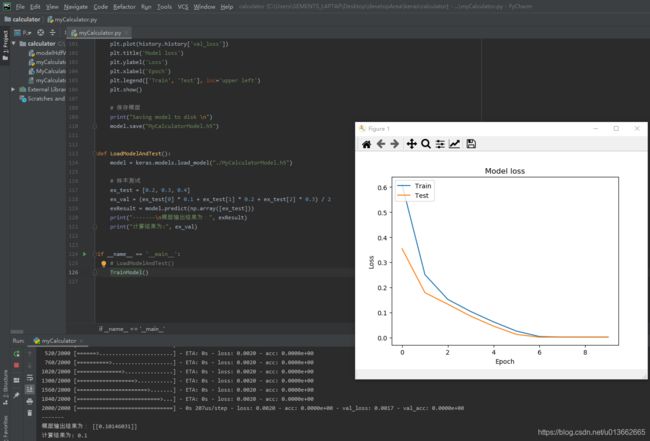
在训练完毕,进行样本测试后,我们将模型的训练历史可视化,观察它的损失值在训练的过程中的变化趋势。
这里我们代码注释掉了之前所写的训练过程中准确率值的历史曲线展示,在模型训练的过程中你也会发现,在pycharm的输出窗口中,模型信息的 acc-即准确率值一直为0。这是有原因的,因为准确率是看模型的输出值是否恰好等于给定的训练数据的标准输出值,若相等则计数,最后进行统计得出当前批次的训练中的准确率。然而我们的模型在训练过程中,直至训练完毕,也不能100%的拟合好期望的输出,最小的损失值目前停留在了0.2%,这意味着在训练过程中,很难碰到刚好我们模型的输出值等于标准输出值,其总是有小数位上略微的差别。因此便无法记录准确率,即使展示历史准确率也只有一条直线而已。
运行,我们便可看到模型训练的结果:
1-4 模型的保存与再载入
在模型训练完毕后,我们将模型进行保存
# 保存模型
print("Saving model to disk \n")
model.save("MyCalculatorModel.h5")这样模型在本地便可保存成为一个 hdf5 格式的文件,其中包含了它的参数信息,这是我们之后所需要的。
而当我们在使用Keras框架,需要再载入之前的模型时,通过调用Keras的函数即可完成模型的载入:
def LoadModelAndTest():
model = keras.models.load_model("./MyCalculatorModel.h5")
# 样本测试
ex_test = [0.2, 0.3, 0.4]
ex_val = (ex_test[0] * 0.1 + ex_test[1] * 0.2 + ex_test[2] * 0.3) / 2
exResult = model.predict(np.array([ex_test]))
print("-------\n模型输出结果为:", exResult)
print("计算结果为:", ex_val)
2 - 部署模型
2-1 模型参数的提取
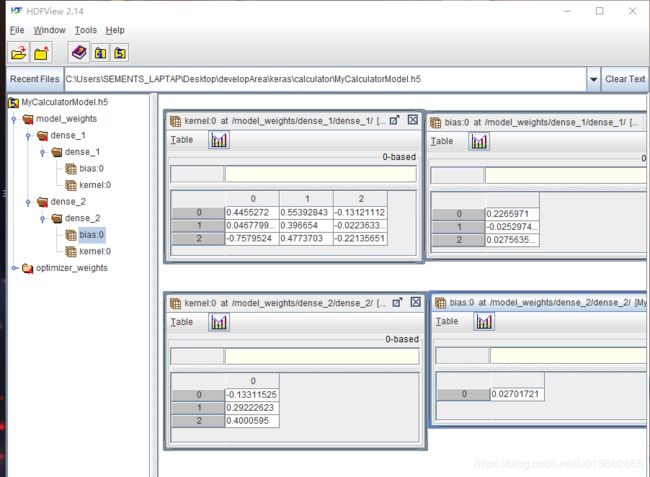
前面我们已经将训练好的模型在本地保存为HDF5格式的文件,为了在单片机上运行,我们首先需要将模型中各个层的权重参数以及偏置参数提取出来。这里推荐使用 HDFView 软件进行查看,可以在这里(https://support.hdfgroup.org/ftp/HDF5/hdf-java/current/bin/)进行下载。
可以看到我们模型中的两层网络的参数,接下来我们研究如何在矩阵运算中使用这些参数。
2-2 矩阵的运算方式
这里的参数,权重与偏置都以矩阵方式进行了保存。在我们的神经网络中,是最简单的多层感知器神经网络,是顺序网络,没有卷积及其他操作,因此我们可以用简单的矩阵运算方法进行运算。
权重矩阵中,每一列为一个下层神经元连接上层神经元的权重值,每一行为一个上层神经元连接下层神经元的权重;而偏置矩阵则是一个一维向量。因此,当输入向量定义为行向量时,将权重矩阵右乘输入行向量,再将得到的行向量加上偏置矩阵的转置即可。
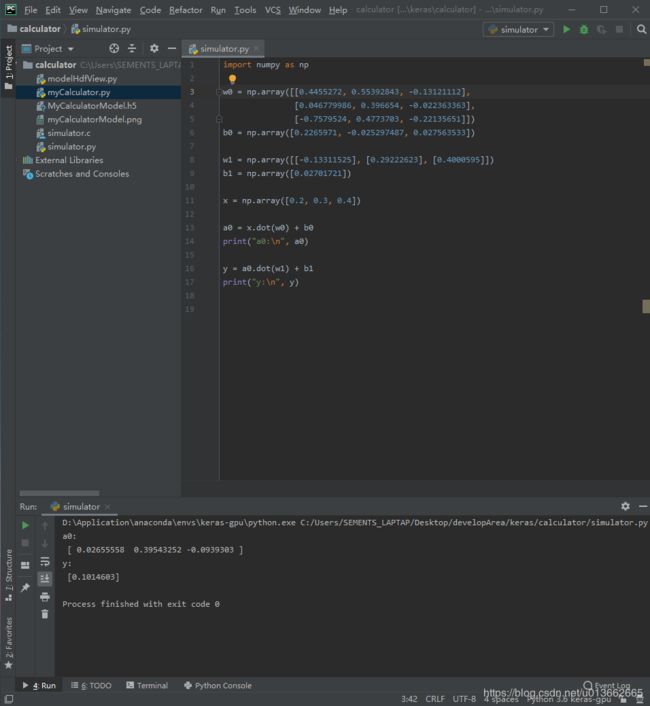
我们可以看一下用python实现的计算:
import numpy as np
w0 = np.array([[0.4455272, 0.55392843, -0.13121112],
[0.046779986, 0.396654, -0.022363363],
[-0.7579524, 0.4773703, -0.22135651]])
b0 = np.array([0.2265971, -0.025297487, 0.027563533])
w1 = np.array([[-0.13311525], [0.29222623], [0.4000595]])
b1 = np.array([0.02701721])
x = np.array([0.2, 0.3, 0.4])
a0 = x.dot(w0) + b0
print("a0:\n", a0)
y = a0.dot(w1) + b1
print("y:\n", y)在代码中,我们手动的将偏置矩阵转换成了一个行向量,这样在后续的代码中直接进行矩阵加法即可。
2-3 NNLayer
NNLayer是我编写的一个用于方便计算这类全连接网络的,使用纯C语言实现的,没有动态内存分配的计算框架。十分适合部署在MCU这类不能够使用动态内存分配,资源紧凑的平台上使用。
目前NNLayer只包含了前向传播的计算,暂时不准备将训练部分融入(用PC进行训练不更方便快捷吗?)以节省代码体积。由于目前只设计涵盖了正对全连接网络的计算,因此它的使用比较简单,只需要调用两个函数,一个进行初始化,一个调用进行预测计算即可:
NNLayer.h
#ifndef _NNLAYER_H_
#define _NNLAYER_H_
#define LAYER_TOTAL 2
#define LAYER_0_INDIM 3
#define LAYER_0_OUTDIM 3
#define LAYER_1_INDIM 3
#define LAYER_1_OUTDIM 1
#include "../common.h"
/*
* NNLayer变量定义
*/
typedef struct
{
const double* weight; //权重二维矩阵 INDIM * OUTDIM
const double* bais; //偏置数组 1 * OUTDIM
int inDim; //输入维数
int outDim; //输出维数
double* outVal; //输出数组
}NNLayer;
void NNLayerInit();
void NNLayerPredict(NNLayer* model,double* x);
#endif
NNLayer.c
#include "NNLayer.h"
extern xdata NNLayer gMyCalculatorModel[LAYER_TOTAL];
extern xdata double gLayer0OutVal[LAYER_0_OUTDIM],gLayer1OutVal[LAYER_1_OUTDIM];
/*
* 训练好的模型参数
*/
const double code W0[LAYER_0_INDIM][LAYER_0_OUTDIM] = {
// nn00 nn01 nn02
{0.4455272 ,0.55392843 ,-0.13121112},
{0.046779986,0.396654 ,-0.022363363},
{-0.7579524 ,0.4773703 ,-0.22135651}
};
const double code B0 [LAYER_0_OUTDIM] = {0.2265971 ,-0.025297487 ,0.027563533};
const double code W1[LAYER_1_INDIM][LAYER_1_OUTDIM] = {
{-0.13311525},
{0.29222623},
{0.4000595}
};
const double code B1[LAYER_1_OUTDIM] = {0.02701721};
/*
* return arr[r][c]
*/
double _getWeight(double* arr,int r,int rNum,int c)
{
return *(arr + r*rNum + c);
}
/*
* NNLayer初始化
* 绑定每层的权重矩阵、偏置矩阵
* 设置每层的输入维度,输出维度
* 绑定每层的输出暂存数组
*/
void NNLayerInit()
{
gMyCalculatorModel[0].weight = W0;
gMyCalculatorModel[0].bais = B0;
gMyCalculatorModel[0].inDim = LAYER_0_INDIM;
gMyCalculatorModel[0].outDim = LAYER_0_OUTDIM;
gMyCalculatorModel[0].outVal = gLayer0OutVal;
gMyCalculatorModel[1].weight = W1;
gMyCalculatorModel[1].bais =B1;
gMyCalculatorModel[1].inDim = LAYER_1_INDIM;
gMyCalculatorModel[1].outDim = LAYER_1_OUTDIM;
gMyCalculatorModel[1].outVal = gLayer1OutVal;
}
/*
* NNLayer进行预测
* model - NNLayer数组
* x - 输入向量,数目符合LAYER_0_INDIM
*/
void NNLayerPredict(NNLayer* model,const double* x)
{
int _indexW,_indexX,_indexLayer;
for(_indexLayer = 0 ; _indexLayer < LAYER_TOTAL ; _indexLayer++)
{
for(_indexW = 0 ; _indexW < model[_indexLayer].outDim ; _indexW++)
{
for(_indexX = 0 ; _indexX < model[_indexLayer].inDim ; _indexX++)
{
if(_indexLayer == 0)
{
model[_indexLayer].outVal[_indexW] += x[_indexX] * _getWeight(model[_indexLayer].weight,_indexX,model[_indexLayer].outDim,_indexW);
}
else
{
model[_indexLayer].outVal[_indexW] += model[_indexLayer - 1].outVal[_indexX] * _getWeight(model[_indexLayer].weight,_indexX,model[_indexLayer].outDim,_indexW);
}
}
model[_indexLayer].outVal[_indexW] += model[_indexLayer].bais[_indexW];
}
}
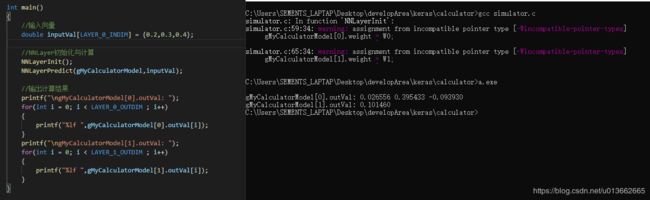
}使用我们刚刚进行训练的模型,将参数导入进行运算:
可以看见很好的复现了我们使用模型进行预测的结果
2-4 在单片机上运行
由于手头只有一块其他项目上测试用到的单片机板,我们只能在这块板子上进行测试。这块板子使用的主控是 STC15F2K60S2,主频设置在20MHZ,板载一块0.96寸12864oled屏幕,可通过电脑USB进行串口通讯。
参照我之前的这篇文章(关于keil-C51中code、idata以及xdata),将较大的字库、以及神经网络模型的参数矩阵之类不需要修改的数组,标记为code字段,保存在代码段中。
编写单片机程序,主要初始化了oled屏幕、串口,并通过NNLayer进行神经网络的初始化与计算:
int main()
{
xdata double inputVal[LAYER_0_INDIM] = {0.2,0.3,0.4};
char str[16];
int i;
//初始化外设
ScreenInit();
UartInit();
UartSend("HelloWorld\r\n");
//NNLayer
NNLayerInit();
NNLayerPredict(gMyCalculatorModel,inputVal);
//结论输出
UartSend("The input is:");
for(i = 0;i < LAYER_0_INDIM;i++)
{
sprintf(str,"%f ",inputVal[i]);
UartSend(str);
}
UartSend("\r\ngMyCalculatorModel[0].outVal: ");
for(i = 0; i < LAYER_0_OUTDIM ; i++)
{
sprintf(str,"%f ",gMyCalculatorModel[0].outVal[i]);
UartSend(str);
}
UartSend("\r\ngMyCalculatorModel[1].outVal: ");
for(i = 0; i < LAYER_1_OUTDIM ; i++)
{
sprintf(str,"%f ",gMyCalculatorModel[1].outVal[i]);
UartSend(str);
}
ScreenFill(SCREEN_BLACK);
ScreenShowASCIIString(0,0,SCREEN_BLACK,"Input Vector:"); //输入
sprintf(str,"%.1f %.1f",inputVal[0],inputVal[1]);
ScreenShowASCIIString(0,2,SCREEN_WHITE,str);sprintf(str,"%.1f",inputVal[2]);ScreenShowASCIIString(64,2,SCREEN_WHITE,str); //scanf的bug,一次只能两
ScreenShowASCIIString(0,4,SCREEN_BLACK,"Predict:"); //输出
sprintf(str,"%f",gMyCalculatorModel[1].outVal[0]);
ScreenShowASCIIString(0,6,SCREEN_WHITE,str);
while(1);
}使用keil4进行编译,烧录到单片机上,我们可以看到单片机的oled屏幕上输出的计算结果:
同时,打开串口调试助手,我们可以看到单片机通过串口发送回的计算结果:
至此,我们完成了神经网络的搭建、训练、参数提取以及移植到51单片机上的步骤。