BP神经网络原理简单介绍以及公式推导（矩阵形式和分量形式）

BP神经网络原理简单介绍以及公式推导

标签（空格分隔）： 神经网络

---

BP神经网络简单介绍

在60年代提出了神经网络概念之后，由于感知机等神经网络无法处理线性不可分问题（比如异或问题）导致人们对神经网络的兴趣大减，认为神经网络的能力有限，只能处理线性可分问题。之后，有人提出了多层神经网络的想法，用于解决异或问题。下面就是用一个两层的神经网络解决异或问题具体方法：

y=ψ(−2v1+v2−0.5)v1=ψ(x1+x2−1.5)v2=ψ(x1+x2−0.5)ψ(x)={1,0,x>0x≤0

y 是网络的输出， v1 和 v2 是隐藏层的两个神经元， x1 和 x2 是输入。下面的表格验证了这个两层的网络可以处理异或问题。

x1	x2	v1	v2	y
0	0	0	0	0
1	0	0	1	1
0	1	0	1	1
1	1	1	1	0

虽然这个两层网络能够处理异或问题，但是当时并没有引起太大的关注，直到80年代， Back Propagation(BP)神经网络的提出，才使得神经网络又重新回到了人们的视线中。

这里，主要想通过一个三层的BP神经网络来说明其原理和公式推导。

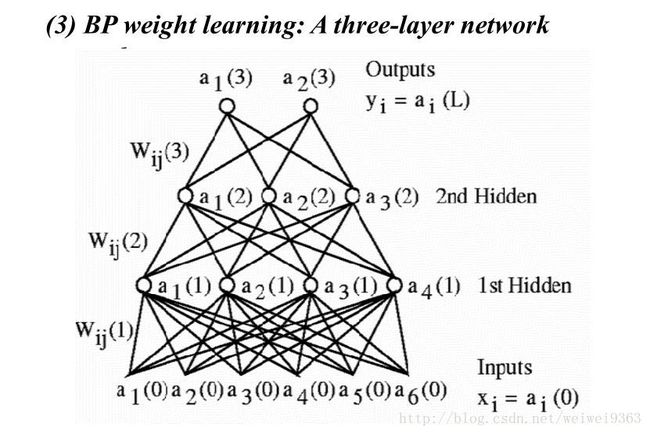
公式推导

我们首先需要对整个网络进行数学建模，然后进行学习算法的描述，我们列举分量和矩阵两种不同形式的求导方式，分量形式刚开始看比较繁琐但是比较简单，矩阵形式结构简单但是涉及到矩阵求导，求导的相关知识需要比较熟悉。

网络的数学描述

首先我们先说一说激活函数的选择，在感知机中，选择的是非线性的带阈值的激活函数，在BP网络中，通常选择的是Sigmoid函数，这类函数的导数有一个很好的性质：自身相关。比如常见的

f(x)=11+e−x

其导数为 f′(x)=f(x)(1−f(x)) ，证明也不难，就是求导，然后进行拼凑就可以了。
接下来我们对这个三层的网络进行数学抽象，可以的话请一个一个的手写一遍，这样能够加深理解它们之间的关系。先是各层的输入和输出变量的定义

input vector:hiden vector:output vector:Y(0)=[x1,x2,⋯,x6]T=[a1(0),a2(0),a3(0),a4(0),a5(0),a6(0)]TY(1)=[a1(1),a2(1),a3(1),a4(1)]TY(2)=[a1(2),a2(2),a3(2)]TY(3)=[a1(3),a2(3)]T

然后，我们一层一层的进行数学描述。

First hiden layernet(1)l=∑k=16W1lky(0)k,(1≤l≤4)net(1)=W(1)Y(0)net(1)=[net(1)1,net(1)2,net(1)3,net(1)4]TW(1)=⎡⎣⎢⎢⎢W(1)11⋮W(1)41⋯⋯⋯W(1)16⋮W(1)46⎤⎦⎥⎥⎥output:Y(1)=[Y(1)1,⋯,Y(1)4]T,where Y(1)=f(1)(net(1))

net(1) 的输入是 Y(0) ，利用 W(1) 得到输出 Y(1) 。在第一层中， k=6 是因为输入层 Y(0) 有六个输入， 1≤l≤4 是因为第一层中有4个神经元，同理第二层和第三层。请注意 net(1) 的和 W(1) 的维数，想一想为什么会这样，你这么聪明一定能想清楚的(输入和输出的个数)。接下来两层与第一层类似，重点在思考清楚 W(n) 和 net(n) 的维数，就能对BP网络结构有一个大致的认识。还是希望各位能手抄一遍。

Second hiden layernet(2)l=∑k=14W2lky(1)k,(1≤l≤3)net(2)=W(2)Y(1)net(2)=[net(2)1,net(2)2,net(2)3]TW(2)=⎡⎣⎢⎢⎢W(2)11⋮W(2)31⋯⋯⋯W(2)14⋮W(2)44⎤⎦⎥⎥⎥output:Y(2)=[Y(2)1,⋯,Y(2)3]T,where Y(2)=f(2)(net(2))

Third hiden layernet(3)l=∑k=13W3lky(2)k,(1≤l≤2)net(3)=W(3)Y(2)net(3)=[net(3)1,net(3)2]TW(3)=⎡⎣⎢⎢⎢W(3)11⋮W(3)21⋯⋯⋯W(3)13⋮W(3)23⎤⎦⎥⎥⎥output:Y(3)=[Y(3)1,Y(3)2]T,where Y(3)=f(3)(net(3))

我们总结一下：
1. 一个 net 包含了一组输入，一组权重，一组输出。对于 net(n) ，它的输入是 Y(n−1) ，利用权重 W(n) 得到输出 Y(n) ，即 net(n)=W(n)Y(n−1)
2. W(n)∈Rq×p ，q是第n层神经元的个数，p是n-1层神经元的个数也就是当前层的输入个数。

公式推导（分量形式）

我们的目标是希望通过调整 W 使得输出和目标有最小的误差，也就是最小二乘的思想

Least-Squared Error: E=12∑l=12(Tl−Y(3)l)2=12∑l=12(δ(3)l)2

其中， δl=(Tl−Y(3)l) 。因为BP网络是反馈式网络，所以在更新权值时是从后向前更新的，所以首先更新的是第三层的权值。
那么 E 和 W(3) 有什么关系呢？通过上面的对网络的数学描述，我们知道

Y(3)=f(3)(net(3))=W(3)Y(2)分量：Y(3)1Y(3)2=f(3)(net(3)1)=f(3)(net(3)2)=∑k=13W31kY(2)k=∑k=13W32kY(2)k

所以有：

E=12∑l=12(Tl−Y(3)l)2=12∑l=12(Tl−f(3)(net(3)l))2=12∑l=12(Tl−∑k=13W3lkY(2)k)2

因此 E 和 W 求导关系为：

∂E∂W(3)lk=∂E∂Y(3)l∂Y(3)l∂net(3)l∂net(3)l∂W(3)lk

其中：

∂E∂Y(3)l=(Yl−Tl)=−δl(1)

∂Y(3)l∂net(3)l=f′(3)(net(3)l)(2)

∂net(3)l∂W(3)lk=Y(2)k(3)

根据（1）、（2）、（3）可得

∂E∂W(3)lk=−δlf′(3)(net(3)l)Y(2)k

我们已经求出单个分量的求导结果，那么对于整个 W(3)

∂EW(3)=⎡⎣⎢⎢⎢⎢⎢∂EW(3)11∂EW(3)21∂EW(3)12∂EW(3)22∂EW(3)13∂EW(3)23⎤⎦⎥⎥⎥⎥⎥=−⎡⎣δ1f′(3)(net(3)1)δ2f′(3)(net(3)2)⎤⎦[Y(2)1Y(2)2Y(2)3]=−S(3)Y(2)T

其中

S(3)=−⎡⎣f′(3)(net(3)l)00f′(3)(net(3)2)⎤⎦⎡⎣δ(3)1δ(3)2⎤⎦=F′(3)(net(3))δ=−∂E∂net(3)

至于 ∂E∂net(3) 怎么求，在后面的矩阵形式分析部分将会说明。
上面已经说明对第三层权值的更新过程，对于第二层权值的更新，最重要的还是理解 E 和 W(2) 之间的关系。
上面只给出第三层的详细求导，第二层和第一层请看老师给的课件（公式编辑太费时间了）下面给出老师课件里的求导，从第三层到第一层，有些地方有点小错误，不过不影响理解。

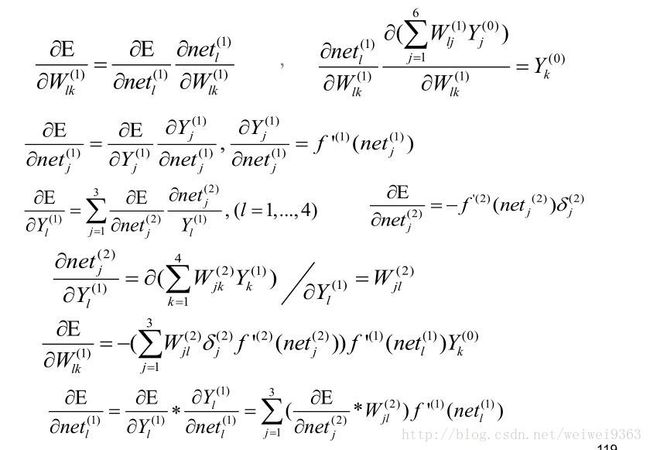
公式求导（矩阵形式）

下面我们用矩阵的形式进行求导，涉及到矩阵求导的相关知识，这里有一些参考资料，希望能够帮到大家：
1. 矩阵求导术（上）
2. 闲话矩阵求导
3. 矩阵求导与迹
4. 向量內积、矩阵內积
首先能量函数改写成：

Least-Squared Error: E=12∥T−Y∥22

第三层更新：
先算 ∂E∂Y(3)

EdE所以: =12(T−Y)T(T−Y)=12(TTT−2TTY+YTY)=12tr(−2TTdY+dYTY+YTdY)=12tr(−2TTdY)+tr(dYTY)+tr(YTdY)=12tr(−2TTdY)+tr(YTdY)+tr(YTdY)=12(−2TT+2YT)dX=tr((Y−T)TdY)∂E∂Y(3)=Y−T=−δ

再算 ∂E∂net(3)

dE所以： 设： =tr((∂E∂Y)TdY)=tr((∂E∂Y)Tdf(3)(net(3)))=tr((∂E∂Y)Tf′(3)(net(3))⊙d(net(3)))=tr((∂E∂Y⊙f′(3)(net(3)))Td(net(3)))=tr((−δ⊙f′(3)(net(3)))Td(net(3)))∂E∂net(3)=−δ⊙f′(3)(net(3))S(3)=δ⊙f′(3)(net(3))=−∂E∂net(3)

最后算 ∂E∂W(3)

dE所以： ∂E∂W(3)=tr((∂E∂net(3))Td(net(3)))=tr((∂E∂net(3))Td(W(3)Y(2)))=tr(Y(2)(∂E∂net(3))Td(W(3)))=∂E∂net(3)Y(2)T=−δ⊙f′(3)(net(3))Y(2)T=−S(3)Y(2)T

第二层更新：
先求 ∂E∂Y(2)

dE所以： =tr((∂E∂net(3))Td(net(3)))=tr((∂E∂net(3))Td(W(3)Y(2)))=tr((∂E∂net(3))TW(3)d(Y(2)))∂E∂Y(2)=W(3)T∂E∂net(3)

再求 ∂E∂net(2)

dE所以： 设： =tr((∂E∂Y(2))TdY(2))=tr((∂E∂Y(2))Tf′(2)(net(2))⊙d(net(2)))=tr((∂E∂Y(2)⊙f′(2)(net(2)))Td(net(2)))∂E∂net(2)=∂E∂Y(2)⊙f′(2)(net(2))=W(3)T∂E∂net(3)⊙f′(2)(net(2))=−W(3)TS(3)⊙f′(2)(net(2))S(2)=W(3)TS(3)⊙f′(2)(net(2))=−∂E∂net(2)

最后求 ∂E∂W(2)

dE所以： =tr((∂E∂net(2))Td(net(2)))=tr((∂E∂net(2))Td(W(2)Y(1)))=tr(Y(1)(∂E∂net(2))Td(W(2)))∂E∂W(2)=∂E∂net(2)Y(1)T=−S(2)Y(1)T

第一层更新：

dE所以： ∂E∂Y(1)=tr(∂E∂net(2)Td(W(2)Y(1)))=tr(∂E∂net(2)TW(2)dY(1))=(W(2))T∂E∂net(2)=−(W(2))TS(2)

dE所以： ∂E∂net(1)=tr(∂E∂Y(1)TdY(1))=tr(∂E∂Y(1)Tdf(1)(net(1)))=tr(∂E∂Y(1)⊙f′(1)(net(1))Td(net(1)))=∂E∂Y(1)⊙f′(1)(net(1))=−(W(2))TS(2)⊙f′(1)(net(1))=−S(1)

dE所以： ∂E∂W(1)=tr(∂E∂net(1)Td(W(1)Y(0)))=tr(Y(0)∂E∂net(1)TdW(1))=∂E∂net(1)(Y(0))T=−S(1)(Y(0))T

以上就是对各层权值 W(i) 的梯度的公式推导了。下面对 θ(i) 推导，因为比较简单，我们就以第三层为例简单说明下。

dE所以： ∂E∂θ(3)=tr(∂E∂net(3)Td(W(3)Y(2)+θ(3)))=tr(∂E∂net(3)Tdθ(3))=∂E∂net(3)=−S(3)

总结

至此，可以对以整个学习算法进行总结了。

下一篇博文将会用MATLAB实现以上算法。