机器学习--BP算法推导理解
首先打卡Ng老师的机器学习,今天是第六天。
昨天晚上在b站看了神经网络那节,Ng老师对于反向传播原理并没有做出解释,听了之后满头问号。幸亏开了弹幕,在各种弹幕发的博客链接的帮助下,今天总算把整个过程搞明白些了。
下面用自己的思路总结梳理一下反向传播的推导过程,完全是一个小白的角度,希望对大家有帮助。
以下推导使用的的符号均与coursera机器学习中采用的符号一致,不同的符号推导结果可能会不同
有关引用已注明出处
为什么要用反向传播
首先来讲一下为什么神经网络里要用反向传播那么复杂的更新权重的方法。
先回顾一下神经网络的代价函数(先不考虑正则):
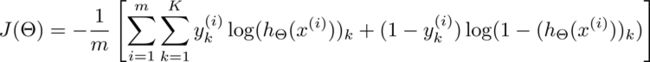
再类比一下逻辑回归:
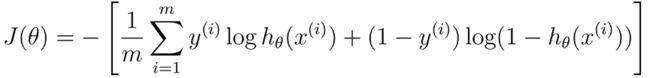
会发现神经网络可以理解为多维的逻辑回归
那么我们接下来考虑神经网络能不能也用类似于梯度下降的思维,也即代价函数J(Θ)对Θ的偏导,算出梯度来呢?
前向传播计算J(Θ)
根据这个思路,我们需要先将样本送入神经网路算出代价函数J(Θ),假设神经网络如下:
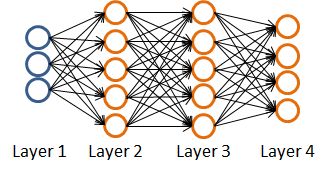
先只考虑样本集里的一个样本(x,y),将其喂给这个模型
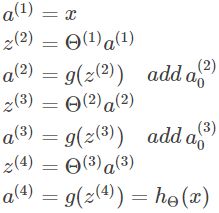
最后算出的hΘ(x) 即为当前模型对于输入x的预测,从而写出代价函数J(Θ)(这里再重复一遍):
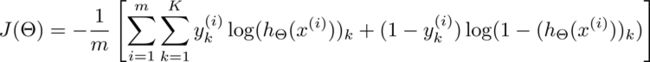
反向传播推导过程:
1.误差值δ与∂Cost/∂z 相等的证明
根据前向传播,我们可以得到代价函数J(Θ)以及所有神经网络里神经元的信息(a、z),接下来我们考虑用代价函数J(Θ)对所有权重求偏导。
假设我们现在有如下神经网络:
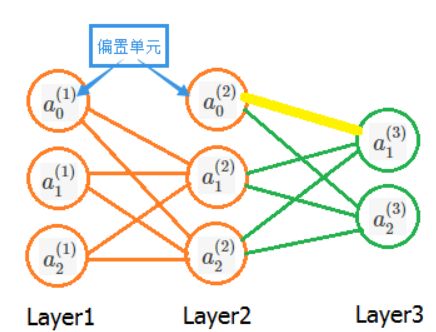
我们先只考虑输入样本集中的一个样本,并且先考虑图中黄色的那条权重,即第二层的偏置单元 a0(2) 的参数 Θ10(2) 。由于该条权重仅仅影响到神经元a1(3) ,而我们要求的是这条权重其对J(Θ)的偏导,因此我们可以取J(Θ)中仅与黄色的这条边 Θ10(2)有关的项。那么数量m、维度k,以及另一个输出 a2(3) 都可以被忽略。即代价函数可以化简为如下形式:
式子里的 hΘ(x) 是最后的预测结果,而 hΘ(x) = g(z) 并且:z1(3)=Θ10(2)a0(2)+Θ11(2)a1(2)+Θ12(2)a2(2)
所以我们对参数 Θ10(2) 求偏导如下:
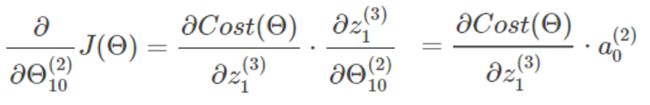
结合上述式子,并进行进一步推导:

此处需求g′(z1(3)),可以先求g′(z),随后将 z=z1(3) 代入即可:
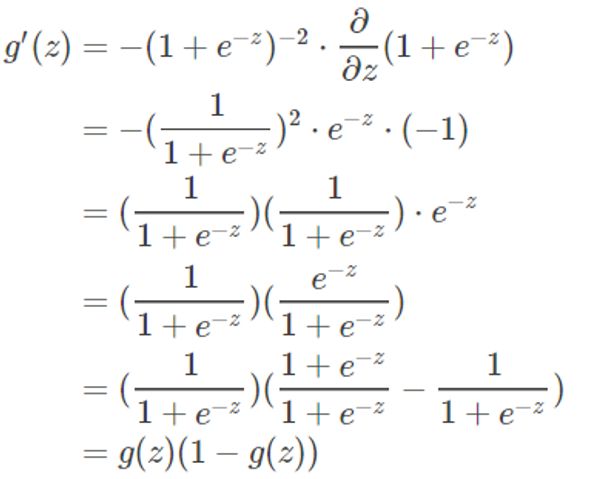
代入 z=z1(3) 可得:
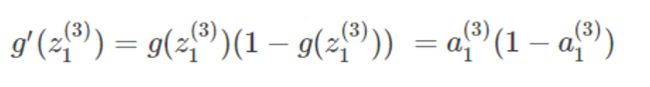
将该式子代回上述黄色箭头处:
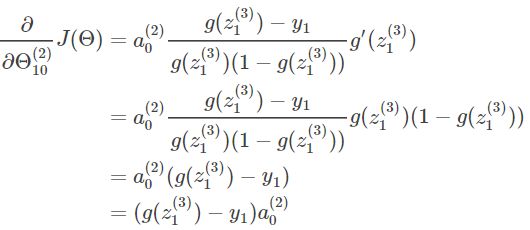
上述结果的 g(z1(3))−y1 是什么?不就是预测结果和真值的误差吗?我们把这个误差记作δ13 ,随后得到一个很重要的结论:
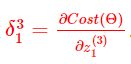
到这里,上述所有推导可以总结为一个式子:
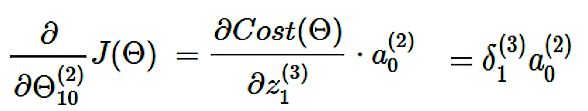
这个结论同样可以推广到神经网络中的任何一个神经元,所以对于任何一个权重对代价函数的偏导:
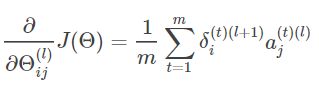
误差δ和偏导的关系的证明也就到此结束,我们将要求的偏导转换为有关误差δ的式子。所以我们面临一个新的问题:误差如何计算
我们可以很简单地得到输出层的误差:
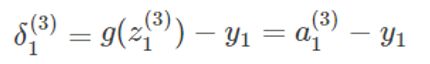
推广到其他神经元:
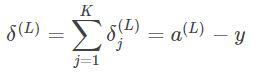
需要注意的是式子中的y指的是真值,而我们只知道输出层真值,对于任何一个输出层以外的神经元,其真值我们无法知晓,因此我们也无法直接用上述公式求出非输出层神经元的δ。
为了求任何一个神经元的误差δij,我们要利用反向传播的最重要的一步——误差的反向传递。
2.误差δ的反向传递
以最简单的三层神经网络为例,其可推广到具有任意层数,且每层有任意个激励单元的神经网络。
假设有如下图神经网络:
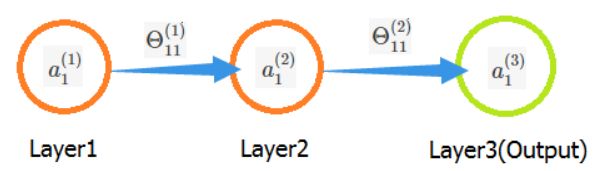
假设我们要求参数 Θ11(1) 关于 J(Θ) 的偏导数,由第一部分的证明我们可以得出结论:
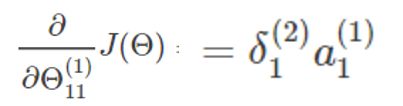
而我们现在并不知道误差值δ1(2),所以我们换个角度考虑。我们现在已知的是输出层,所以尽量能够把问题和已知的输出层联系起来,所以我们的目光从右向左看过来。运用链式求导可知:
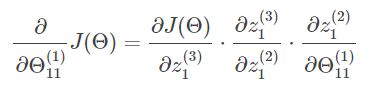
其中:
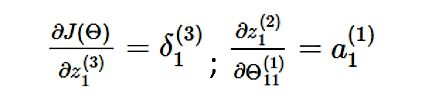
所以:
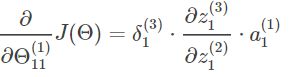
将式子进一步化简:
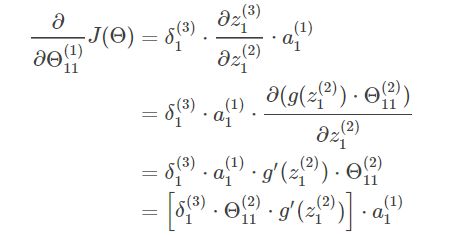
和我们第一部分的结论结合起来可以得到:
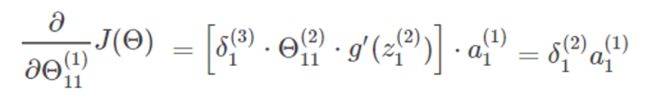
因此,我们又得到了一个重要的结论,即误差传递公式:
推广到一般形式:
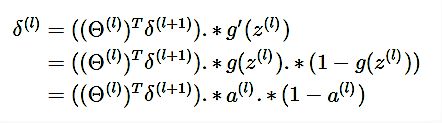
而任何一个神经元的误差 δij 求出,也就求出了任何一条权重Θ对代价函数的偏导。
结合加入正则项后神经网络的误差公式:
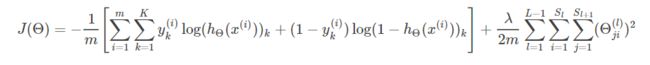
即可得到求任意参数 Θij(l) 的偏导数的公式:
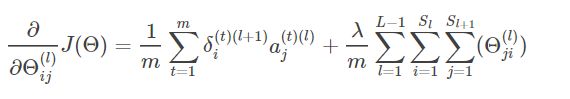
3.m个训练样本累加
到这里,有关于误差、梯度的关系以及误差传递的推导也就结束了,但是这仅仅是对于一个样本,而仅仅一个样本对于模型权重更新起到的作用是不够准确的,因此我们假设取训练集中m个样本为一个周期,即对进行m次反向传播产生的效应进行累加,取平均效应,这也就是Ng老师ppt上的结论:

Δij(l) 表示的是所有m个样本训练累加产生的效应,一开始Δij(l)为0,m重循环结束,对累加得Δij(l) 取平均,再加上正则项,得到m个训练样本的平均效应D:
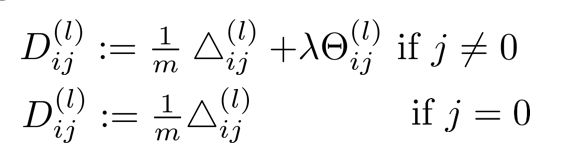
Dij(l) 即表示m个样本对于模型训练产生的更新(可以暂时理解为梯度),最后将用这个Dij(l) 更新第(L-1)~第L层的权重,其他层与其一致。
上述过程即可总结为:

本文参考图文资料来源:
机器学习笔记07:神经网络的反向传播(Backpropagation)
吴恩达机器学习ppt课件
