js二叉树的基本算法操作
二叉树
二叉树的基本实现,删除两个节点的地方还是不太熟,还要好好学习一下才行
数据结构里关于链和树这块,最开始看视频的时候最好跟着老师敲一次代码,对于不会举一反三的码畜来说会更好的知道对象的属性是个啥。我一度搞不定树的两条边怎么表示的,哈哈
1.封装二叉树
function BinarySearchTree() {
function node(key) {
this.key = key;
this.left = null;
this.right = null;
}
this.root = null;
}2插入二叉树
// 插入节点
BinarySearchTree.prototype.insert = function (key) {
var newNode = new Node(key);
if (this.root == null) {
this.root = newNode;
} else {
this.insertNode(this.root, newNode);
}
}
BinarySearchTree.prototype.insertNode = function (node, newNode) {
if (newMode.key < node.key) { // 向左查找
if (node.left == null) {
node.left = newNode
} else {
this.insertNode(node.left, newNode)
}
} else { // 向右查找
if (node.right == null) {
node.right = newNode
} else {
this.insertNode(node.right, newNode);
}
}
}3.遍历二叉树
//handler 处理经过的函数 ,先序遍历
BinarySearchTree.prototype.preOrderTraversal = function (handler) {
this.preOrderTravesalNode(this.root, handler)
}
BinarySearchTree.prototype.preOrderTraverSalNode = function (node, handler) {
if (node != null) {
// 在此函数里输出高度
handler(node.key)
this.preOrderTraversalNode(node.left, handler);
this.preOrderTraversalNode(node.rigth, handler);
}
}
//handler 处理经过的函数 ,中序遍历
BinarySearchTree.prototype.midOrderTraversal = function (handler) {
this.midOrderTravesalNode(this.root, handler)
}
BinarySearchTree.prototype.midOrderTraverSalNode = function (node, handler) {
if (node != null) {
// 在此函数里输出高度
this.midOrderTraverSalNode(node.left, handler);
handler(node.key)
this.midOrderTraverSalNode(node.rigth, handler);
}
}
//handler 处理经过的函数 ,后序遍历
BinarySearchTree.prototype.afterOrderTraversal = function (handler) {
this.afterOrderTraverSalNode(this.root, handler)
}
BinarySearchTree.prototype.afterOrderTraverSalNode = function (node, handler) {
if (node != null) {
// 在此函数里输出高度
this.afterOrderTraverSalNode(node.left, handler);
this.afterOrderTraverSalNode(node.rigth, handler);
handler(node.key)
}
}4.求最大值最小值
// 根据二叉树右边为大的特点
BinarySearchTree.prototype.max = function () {
var node = this.root;
var key = null;
while (node != null) {
key = node.key
node = node.right
}
return key
}
BinarySearchTree.prototype.min = function () {
var node = this.root
var key = null
while (node != null) {
key = node.key;
node = node.left;
}
return key;
}4.搜索二叉树
BinarySearchTree.prototype.search = function (key) {
var node = this.root
while (node != null) {
if (key < node.left) {
node = node.left;
} else if (key > node.left) {
node = node.right
} else {
return true
}
}
return false;
}5.删除二叉树
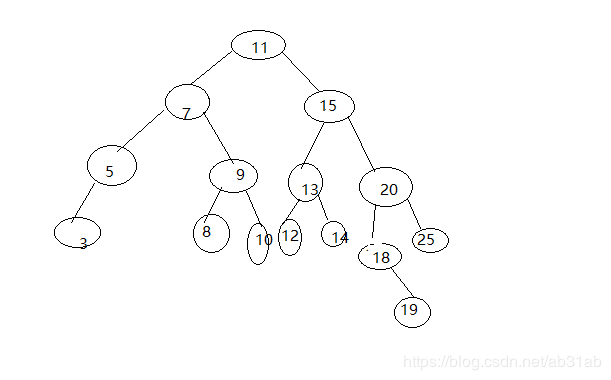
此处列举一下删除两个节点的方法
第一种情况;删除节点9
如果删除节点9,找到后继节点(successor)8,8要替换9,8在删除节点的右边
节点的父节点(parent)7的右节点指向后继节点8,
后继节点的右节点指向删除节点的右节点。
后继节点的左节点指向删除节点的左节点8,指向自身null
第二中情况 删除节点11
如果删除根节点11,找到后继节点,10,10在删除节点的左边
后继节点的左节点指向删除节点的左节点
后继节点的右节点指向删除节点的右节点
第三中情况 删除节点7
1. 找到后继节点8,删除节点的父节点11的左节点指向后继节点,
后继节点的右节点8指向删除节点的右节点9。
后继节点的左节点指向删除节点的左节点5
2.找到后继节点5,删除节点的父节点11的左节点指向后继节点,
后继节点的右节点指向删除节点的右节点9。
第四中情况 删除节点15
1.找到后继节点18, 删除节点的父节点11的右节点指向后继节点18,
后继节点的父节点20的左节点指向后继节点的右节点。
后继节点的左节点指向删除节点的左节点13。
BinarySearchTree.prototype.remove=function(key){
var current=this.root
var parent=null
var isLeftChild=true
while(current.key!=key){
parent=current
if(key