Dijkstra也叫迪杰斯特拉,是典型最短路径算法,计算一个起始节点到路径中其他所有节点的最短路径的算法和思想。在一些专业课程中如数据结构,图论,运筹学等都有介绍。其思想是一种基础的求最短路径的算法,通过基础思想的变化可以解决很多复杂问题,如导航线路,动态规划等。
Dijkstra 算法思想介绍
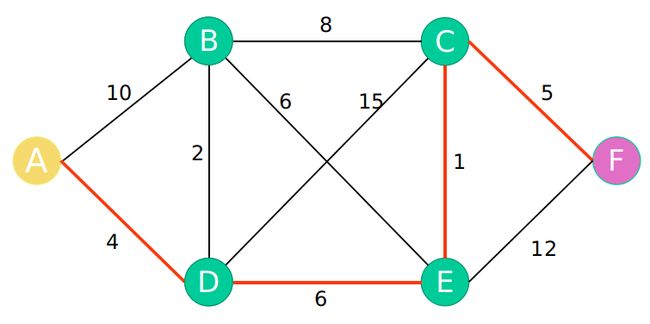
如下图是一个多节点,多路径图。下面以该图为例子讲解dijkstra算法寻找最短路径的过程。

以A点为起始点,求A点到其他点 B C D E F 5个点的最短路径,最后得出A到其他点的最短路径。
因为要求A到其他5个点的最短距离,所以构造一个数组记录A到B C D E F 5个点的路径距离。约定:
- 如果A能够直接达到节点,则使用路径长度即权值作为其距离
- 如果A节点不能直接达到节点则使用无穷大表示A到该点距离。
- 任何点到自身都为0
那么在最开始时,A点到图中所有点的距离数组如下:
| A | B | C | D | E | F |
|---|---|---|---|---|---|
| 0 | 10 | 无穷大 | 4 | 无穷大 | 无穷大 |
dijkstra的算法思想是从以上最短距离数组中每次选择一个最近的点,将其作为下一个点,然后重新计算从起始点经过该点到其他所有点的距离,更新最短距离数据。已经选取过的点就是确定了最短路径的点,不再参与下一次计算。

可能看到这里你完全不明白dijkstra算法的思想,心里可能想:这是说的人话吗?不要紧,如果算法一句话就能解释清楚,那就不会出现那么多算法书了。下面我们就从实际的选取过程中理解这个思想的精髓。
第一次选取
构建好的数组是这样的:
| A | B | C | D | E | F |
|---|---|---|---|---|---|
| 0 | 10 | 无穷大 | 4 | 无穷大 | 无穷大 |
第一步选取该最短路径数组中值最小的一个点。因为A点到本身不需要参与运算,所以从剩下的点中选择最短的一个是D。
第二步以A-D的距离为最近距离更新A点到所有点的距离。即相当于A点经过D点,计算A到其他点的距离。
A-A : 0
A-B : A-D-B:6
A-C : A-D-C:19
A-D : A-D:4
A-E : A-D-E:10
A-F : A-D-F:去穷大
| A | B | C | D | E | F |
|---|---|---|---|---|---|
| 0 | 6 | 19 | 4 | 10 | 无穷大 |
将现在A到各个点的距离和之前的比较,到相同点取最小值。更新了B C E的距离,得到如下新的最短距离数组:
| A | B | C | D | E | F |
|---|---|---|---|---|---|
| 0 | 6 | 19 | 4 | 10 | 无穷大 |
同时现在A D两点已经计算过,不参与下面的计算。
第二次选取
第二次选取的数组为第一次中更新过最短距离的数组
| A | B | C | D | E | F |
|---|---|---|---|---|---|
| 0 | 6 | 19 | 4 | 10 | 无穷大 |
第一步:因为A D 不参与选取,所有从剩下的点中选取最近距离是点B
第二步:以B为最新点,更新最短数组
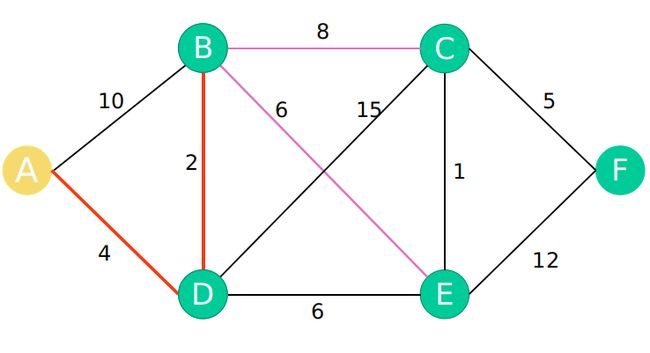
A-A : 0
A-B : A-D-B:6
A-C : A-D-B-C:14
A-D : A-D:4
A-E : A-D-B-E:12
A-F : A-D-B-F:无穷大
| A | B | C | D | E | F |
|---|---|---|---|---|---|
| 0 | 6 | 14 | 4 | 12 | 无穷大 |
对比现在的最短距离和上一个数组的距离,到相同节点取最小的,C点由19更新成14,E点走A-D-E为10,距离更短所以不更新(敲黑板,这个重要),得到如下数组:
| A | B | C | D | E | F |
|---|---|---|---|---|---|
| 0 | 6 | 14 | 4 | 10 | 无穷大 |
此时B点加入最短路径范围中。
第三次选取
上一步得到的数组为:
| A | B | C | D | E | F |
|---|---|---|---|---|---|
| 0 | 6 | 14 | 4 | 10 | 无穷大 |
第一步:选取除了A B D节点之外的剩余节点中最短节点,为点E
第二步:以E点为最新节点,更新最短路径数组

因为在上一部中计算达到E点的距离时没有更新距离,A-D-E 为10 最短,所以更新E点到B C F点的距离时走的路径是A-D-E。注意这里的最短距离有对应的路径,选择最小值就是选择最短距离。
A-A : 0
A-B : A-D-B:6
A-C : A-D-E-C:11
A-D : A-D:4
A-E : A-D-E:10
A-F : A-D-E-F:22
| A | B | C | D | E | F |
|---|---|---|---|---|---|
| 0 | 6 | 11 | 4 | 10 | 22 |
对比现在的最短距离和上一个数组的距离,到相同节点取最小的,更新C点走A-D-E-C 为11,比之前的A-D-B-C14距离更近,更新到F点距离,得到如下数组:
| A | B | C | D | E | F |
|---|---|---|---|---|---|
| 0 | 6 | 11 | 4 | 10 | 22 |
此时E点加入最短路径范围中。
第四次选取
| A | B | C | D | E | F |
|---|---|---|---|---|---|
| 0 | 6 | 11 | 4 | 10 | 22 |
第一步:选取除了A B D E节点之外的剩余节点中最短节点,为点C
第二步:以C点为最新节点,更新最短路径数组
A-A : 0
A-B : A-D-B:6
A-C : A-D-E-C:11
A-D : 4
A-E : A-D-E:10
A-F : A-D-E-C-F:16
| A | B | C | D | E | F |
|---|---|---|---|---|---|
| 0 | 6 | 11 | 4 | 10 | 16 |
对比现在的最短距离和上一个数组的距离,到相同节点取最小的,更新到F点距离,可以得到如下数组:
| A | B | C | D | E | F |
|---|---|---|---|---|---|
| 0 | 6 | 11 | 4 | 10 | 16 |
第五次选取
| A | B | C | D | E | F |
|---|---|---|---|---|---|
| 0 | 6 | 11 | 4 | 10 | 16 |
第一步:选取除了A B C D E节点之外的剩余节点中最短节点,也就是最后一个节点:F
第二步:以F点为最新节点,更新最短路径数组。由于F点是最后一个点,所以也不用更新数组,目前的数组就是所求数组
将F点加入最短路径范围中,此时所有的点都加入了最短路径范围,也就是说A点到所有点的距离都找到了。最总得出的距离值为:

最终得到的结果为:
| A | B | C | D | E | F |
|---|---|---|---|---|---|
| 0 | 6 | 11 | 4 | 10 | 16 |
最终结果
相应的A点到所有点的最短路径走法最终得到的结果为:
| A | B | C | D | E | F |
|---|---|---|---|---|---|
| 0 | 6 | 11 | 4 | 10 | 16 |
算法总结
Dijkstra算法作为求最短路径的经典算法,个人理解为算法提供了一种思想,每走一步都是找到最短的路径,并且每走一步都实时更新所有距离,保证每次都选择最短路径。
python实现Dijkstra
将以上的过程使用python来实现。
首先总结一个Dijkstra算法的核心思想,分成两步走:
- 构造一个最短路径数组,每次找到数组中未访问的节点里最小的点
- 以上一步的节点为最新节点,更新起始点到所有点的距离
使用python就是实现这两步即可
数据准备
二维矩阵
如何描述一个图呢?通常有两种方式,分别是:十字链表和二维矩阵。因为二维矩阵更加直观,所以选择二维矩阵。
将上面的图描述成一个二维矩阵

无穷大使用MAX = float('inf')表示,该数值是python中表示无穷大的一个值。

这个二维矩阵真正直观之处在哪里呢?是能够看到任意一个点到其他点的距离。如想看D点到其他点的距离,就是:

在我们的算法两步走中第二步要更新A点经过某点到其他点的距离,正是使用了这个特征。
MAX= float('inf')
matrix = [
[0,10,MAX,4,MAX,MAX],
[10,0,8,2,6,MAX],
[MAX,8,10,15,1,5],
[4,2,15,0,6,MAX],
[MAX,6,1,6,0,12],
[MAX,MAX,5,MAX,12,0]
]
最短路径数组
在上面讲解算法过程中有一个重要的的最短路径数组,不断更新该数组直到所有的点都被访问到。使用python语言,构造该数组:
distance = [MAX] * len(matrix)
len(matrix) 实际上算出的图的点的个数。初始化时所有的节点都是不可达。
在算法过程中还有一个重要的数组,并没有体现出来,但是在python计算时也很重要,那就是访问过的点。每一次访问之后就要将访问过的点加入到该数组中,这样做是为了避免重复访问。
used_node = [False] * len(matrix)
初始化时认为所有点都没有访问到
代码实现
MAX= float('inf')
matrix = [
[0,10,MAX,4,MAX,MAX],
[10,0,8,2,6,MAX],
[MAX,8,10,15,1,5],
[4,2,15,0,6,MAX],
[MAX,6,1,6,0,12],
[MAX,MAX,5,MAX,12,0]
]
def dijkstra(matrix, start_node):
#矩阵一维数组的长度,即节点的个数
matrix_length = len(matrix)
#访问过的节点数组
used_node = [False] * matrix_length
#最短路径距离数组
distance = [MAX] * matrix_length
#初始化,将起始节点的最短路径修改成0
distance[start_node] = 0
#将访问节点中未访问的个数作为循环值,其实也可以用个点长度代替。
while used_node.count(False):
min_value = float('inf')
min_value_index = 999
#在最短路径节点中找到最小值,已经访问过的不在参与循环。
#得到最小值下标,每循环一次肯定有一个最小值
for index in range(matrix_length):
if not used_node[index] and distance[index] < min_value:
min_value = distance[index]
min_value_index = index
#将访问节点数组对应的值修改成True,标志其已经访问过了
used_node[min_value_index] = True
#更新distance数组。
#以B点为例:distance[x] 起始点达到B点的距离,
#distance[min_value_index] + matrix[min_value_index][index] 是起始点经过某点达到B点的距离,比较两个值,取较小的那个。
for index in range(matrix_length):
distance[index] = min(distance[index], distance[min_value_index] + matrix[min_value_index][index])
return distance
start_node = int(input('请输入起始节点:'))
result = dijkstra(matrix,start_node)
print('起始节点到其他点距离:%s' % result)
结果:
请输入起始节点:0
起始节点到其他点距离:[0, 6, 11, 4, 10, 16]
简单总结
学习python实现Dijkstra重要的地方有几点:
- 数据构造 二维矩阵表示图
- 图的访问方式 更新最短路径数组的过程无非就是分别比较二维矩阵数组中某一行的值和最短路径数组的值
熟悉这样的处理方式,再有类似的算法也能找到解决的思路。例如一个二维矩阵,从起始点开始只能走向下的相邻的元素,求达到某点的最短路径。
希望通过该篇文章,能够深刻理解Dijkstra算法,做到心中有数,手中有活。