深度学习之——KNN算法(k-最近邻算法)
k-最近邻算法
- 基础理论
- 欧式距离(Euclidean distance)
- 曼哈顿距离(Manhattan distance)
- 代码实例
在学习深度和图像识别的时候,看见了一个比较有意思的算法——KNN算法,该算法是图像分类中最简单的算法之一。
基础理论
KNN算法全称是K-最近邻算法,英文名称是K-NearestNeighbor,简称为KNN;从算法名称上,可以猜出,是找到最近的k个邻居,在选取到的k个样本中选取出最近的且占比最高的类别作为预测类别。如下图所示:
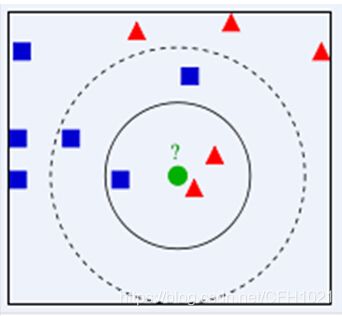
上图所指示,蓝色的正方形和红色的三角形是已经存在的样本,而绿色的圆(待测样本)是要被赋予为那种类别,即是红色的三角形还是蓝色的正方形。如果取 k = 3 k=3 k=3,通过上图可以看出,红色的三角形占比为 2 3 \frac{2}3 32,蓝色正方形占比为 1 3 \frac{1}3 31,因为红色三角形的占比大于蓝色正方形的占比,所以绿色的圆将被赋予为红色三角形的类别。如果取 k = 5 k=5 k=5,通过上图可以看出,红色的三角形占比为 2 5 \frac{2}5 52,蓝色正方形占比为 3 5 \frac{3}5 53,因为红色三角形的占比小于蓝色正方形的占比,所以绿色的圆将被赋予为蓝色正方形的类别。
KNN算法的计算逻辑总结:
- 给定测试对象,计算它与训练集中每个对象的距离;
- 确定最近的k个训练对象,作为测试对象的邻居;、
- 根据这k个训练对象所属的类别,找到占比最高的类别作为测试对象的预测类别。
在KNN算法中,你会发现影像KNN算法准确度的因素主要有两个:一是计算测试对象与训练集中各个对象间的距离;二是k的个数的选择。
主要有两种距离计算方式:曼哈顿距离和欧式距离
欧式距离(Euclidean distance)
d ( x , y ) = ( x 1 − y 1 ) 2 + ( x 2 − y 2 ) 2 + ( x 3 − y 3 ) 2 + . . . + ( x n − y n ) 2 = ∑ i = 1 n ( x i − y i ) 2 d(x,y) =\sqrt{(x_1-y_1)^2 + (x_2-y_2)^2 + (x_3-y_3)^2 + ... + (x_n-y_n)^2} =\sqrt{\displaystyle \sum^{n}_{i=1}{(x_i-y_i)^2}} d(x,y)=(x1−y1)2+(x2−y2)2+(x3−y3)2+...+(xn−yn)2=i=1∑n(xi−yi)2
缺点:它将样本的不同属性(即各指标或各变量量纲)之间的差别等同看待,这一点有时不能满足实际要求。比如年龄和学历对工资的影响,将年龄和学历同等看待;收入单位为元和收入单位为万元同等看待。
标准化欧式距离,将属性进行标准化处理,区间设置在[0,1]之间,减少量纲的影响
曼哈顿距离(Manhattan distance)
d 12 = ∣ x 11 − x 21 ∣ + ∣ x 12 − x 22 ∣ + ∣ x 13 − x 24 ∣ + . . . + ∣ x 1 k − x 2 k ∣ = ∑ k = 1 ∣ x 1 k − x 2 k ∣ d_{12} =|x_{11}-x_{21}| + |x_{12}-x_{22}| + |x_{13}-x_{24}| + ... + |x_{1k}-x_{2k}| =\displaystyle \sum^{}_{k=1}{|x_{1k}-x_{2k}|} d12=∣x11−x21∣+∣x12−x22∣+∣x13−x24∣+...+∣x1k−x2k∣=k=1∑∣x1k−x2k∣
代码实例
import matplotlib.pyplot as plt
import numpy as np
import operator
def KNN_distance(k, dis, trains_1, labels_2, test):
#曼哈顿距离(Manhattan distance): 简称M
#欧式距离(Euclidean Metric): 简称E
assert dis == 'M' or dis == 'E'
count = test.shape[0]
label_list = []
# 欧式距离 sqrt((x1-x2)^2 + (y1-y2)^2)
if dis == 'E':
for i in range(count):
distance = np.sqrt(np.sum(((trains_1 - np.tile(test[i], (trains_1.shape[0], 1))) ** 2), axis=1))
nearest_k = np.argsort(distance)
topK = nearest_k[:k]
classCount = {}
for i in topK:
classCount[labels_2[i]] = classCount.get(labels_2[i], 0) + 1
sortedClassCount = sorted(classCount.items(), key=operator.itemgetter(1), reverse=True)
label_list.append(sortedClassCount[0][0])
# 曼哈顿距离:|x1-x2| + |y1-y2|
elif dis == 'M':
for i in range(count):
distance = np.sum(np.abs(trains_1 - np.tile(test[i], (trains_1.shape[0], 1))), axis=1)
nearest_k = np.argsort(distance)
topK = nearest_k[:k]
classCount = {}
for i in topK:
classCount[labels_2[i]] = classCount.get(labels_2[i], 0) + 1
sortedClassCount = sorted(classCount.items(), key=operator.itemgetter(1), reverse=True)
label_list.append(sortedClassCount[0][0])
return label_list
def CreatDataSet():
# group = np.array([[0.2, 1], [0.3, 4], [0.4, 2], [1, 0.2], [3, 0.5], [5, 0.7]])
group = np.array([[1.0, 2.0], [1.2, 0.1], [0.1, 1.4], [0.3, 3.5], [1.1, 1.0], [0.5, 1.5]])
labels = np.array(['A', 'A', 'B', 'B', 'A', 'B'])
return (group, labels)
if __name__ == '__main__':
group, labels = CreatDataSet()
# 绘制点在坐标系中的位置
# plt.scatter(group[labels == 'A', 0], group[labels == 'A', 1], color='r', marker='*')
# plt.scatter(group[labels == 'B', 0], group[labels == 'B', 1], color='g', marker='+')
# plt.show()
# 欧氏距离
y_test_pred = KNN_distance(2, 'E', group, labels, np.array([[1.0, 2.1], [0.4, 2.0]]))
print(y_test_pred)
print("****************************")
# 曼哈顿距离
y_test_pred = KNN_distance(2, 'M', group, labels, np.array([[1.0, 2.1], [0.4, 2.0]]))
print(y_test_pred)
# output:
# ['A', 'B']
# ****************************
# ['A', 'A']
从输出结果上看,两次的输出结果是不同的,正常情况下应该输出一致, 下面会有一个简单的分析,若有想深入了解的,可以深入研究,
欧式距离: ( 0.6 ) 2 + ( 0 ) 2 \sqrt{(0.6)^2 + (0)^2} (0.6)2+(0)2 和 ( 0.5 ) 2 + ( 0.1 ) 2 \sqrt{(0.5)^2 + (0.1)^2} (0.5)2+(0.1)2 是不相同的
曼哈顿距离: ∣ 0.6 + 0 ∣ |0.6 + 0| ∣0.6+0∣ 和 ∣ 0.5 + 0.1 ∣ |0.5 + 0.1| ∣0.5+0.1∣ 是相同的