【天池】WineQuality葡萄酒品质--数据分析练习
目录
- 一、问题描述
- 1、数据集
- 2、分析思路
- 二、数据分析(Python)
- 0.数据清洗
- 1.分类讨论
- 1-1 描述统计
- 1-2 第一类(基本指标)
- 1-2-1 酸度
- 1-2-2 残留糖
- 1-2-3 酒精
- 1-3 第二类(附加指标)
- 1-3-1 矿物盐
- 1-3-2 二氧化硫
- 1-4 第三类(密度)
- 2.综合分析
- 2-1 各变量间关系
- 2-2 主成分分析
- 3.总结
- 参考资料
一、问题描述
1、数据集
数据下载地址:Wine Quality
根据数据说明可知,Wine Quality数据集中包含两个数据子集,分别是红葡萄酒(red wine)和白葡萄酒(white wine)的样本,样本量如下:
| 数据集 | 数据量 |
|---|---|
| 红葡萄酒(red wine) | 1599 |
| 白葡萄酒(white wine) | 4898 |
每个样本数据的输入、输出规则都是一样的,其中输入条件包含11个客观条件,都是葡萄酒的物化性质,记录为数值;输出结果只有1个,那就是专业品酒师的主观评分(至少取到三次评分的中位数),评分跨度0—10分,0分代表非常糟糕,10分代表非常出色。输入输出指标说明如下:
| 输入指标 | 说明 |
|---|---|
| fixed acidity | 固定酸 |
| volatile acidity | 挥发性酸 |
| citric acid | 柠檬酸 |
| residual sugar | 残留糖 |
| chlorides | 氯化物 |
| free sulfur dioxide | 游离二氧化硫 |
| total sulfur dioxide | 二氧化硫总量 |
| density | 密度 |
| pH | 酸碱值 |
| sulphates | 硫酸盐 |
| alcohol | 酒精 |
| 输出指标 | 说明 |
|---|---|
| quality | 品质(得分介于0-10) |
另外还需要了解到,试验中提供的葡萄酒都来自于葡萄牙的"Vinho Verde"葡萄酒,但葡萄酒的质量并不是均匀分布的,即普通的葡萄酒要远多于劣质葡萄酒或优质葡萄酒,因此可以通过离群点有效甄别出那些少量的劣质葡萄酒或优质葡萄酒。
数据说明原文如下:
Citation Request:
This dataset is public available for research. The details are described in [Cortez et al., 2009].
Please include this citation if you plan to use this database:
P. Cortez, A. Cerdeira, F. Almeida, T. Matos and J. Reis.
Modeling wine preferences by data mining from physicochemical properties.
In Decision Support Systems, Elsevier, 47(4):547-553. ISSN: 0167-9236.
Available at: [@Elsevier] http://dx.doi.org/10.1016/j.dss.2009.05.016
[Pre-press (pdf)] http://www3.dsi.uminho.pt/pcortez/winequality09.pdf
[bib] http://www3.dsi.uminho.pt/pcortez/dss09.bib
1. Title: Wine Quality
2. Sources
Created by: Paulo Cortez (Univ. Minho), Antonio Cerdeira, Fernando Almeida, Telmo Matos and Jose Reis (CVRVV) @ 2009
3. Past Usage:
P. Cortez, A. Cerdeira, F. Almeida, T. Matos and J. Reis.
Modeling wine preferences by data mining from physicochemical properties.
In Decision Support Systems, Elsevier, 47(4):547-553. ISSN: 0167-9236.
In the above reference, two datasets were created, using red and white wine samples.
The inputs include objective tests (e.g. PH values) and the output is based on sensory data
(median of at least 3 evaluations made by wine experts). Each expert graded the wine quality
between 0 (very bad) and 10 (very excellent). Several data mining methods were applied to model
these datasets under a regression approach. The support vector machine model achieved the
best results. Several metrics were computed: MAD, confusion matrix for a fixed error tolerance (T),
etc. Also, we plot the relative importances of the input variables (as measured by a sensitivity
analysis procedure).
4. Relevant Information:
The two datasets are related to red and white variants of the Portuguese "Vinho Verde" wine.
For more details, consult: http://www.vinhoverde.pt/en/ or the reference [Cortez et al., 2009].
Due to privacy and logistic issues, only physicochemical (inputs) and sensory (the output) variables
are available (e.g. there is no data about grape types, wine brand, wine selling price, etc.).
These datasets can be viewed as classification or regression tasks.
The classes are ordered and not balanced (e.g. there are munch more normal wines than
excellent or poor ones). Outlier detection algorithms could be used to detect the few excellent
or poor wines. Also, we are not sure if all input variables are relevant. So
it could be interesting to test feature selection methods.
5. Number of Instances: red wine - 1599; white wine - 4898.
6. Number of Attributes: 11 + output attribute
Note: several of the attributes may be correlated, thus it makes sense to apply some sort of
feature selection.
7. Attribute information:
For more information, read [Cortez et al., 2009].
Input variables (based on physicochemical tests):
1 - fixed acidity
2 - volatile acidity
3 - citric acid
4 - residual sugar
5 - chlorides
6 - free sulfur dioxide
7 - total sulfur dioxide
8 - density
9 - pH
10 - sulphates
11 - alcohol
Output variable (based on sensory data):
12 - quality (score between 0 and 10)
8. Missing Attribute Values: None
2、分析思路
因为这次数据量不大,就不进数据库了,直接使用python进行分析。
由于对葡萄酒不太了解,先去百度一下可以知道以下有用信息:
以下数值标准主要参考自最新国家标准:《葡萄酒》(GB 15037-2006)》,国外标准有别于国内,仅供参考。
-
葡萄酒的四大基本特征:酸度、单宁、酒精和甜味。优质的葡萄酒的四个基本特征一定都是处于很好的平衡状态。
-
酸主要可分为固定酸和挥发酸,常说的总酸就是两者的总和。葡萄酒中含有许多种酸,主要是酒石酸、苹果酸、柠檬酸、琥珀酸、乳酸、醋酸,挥发酸是葡萄酒中以游离状态或以盐的形式存在的所有乙酸等脂肪酸的总和,但不包括乳酸、琥珀酸以及CO2和SO2,其中醋酸是主要的挥发酸。挥发酸的含量是葡萄酒健康状态的“体温表”,因为它是发酵、贮藏管理不良留下的标记,通过挥发酸含量的测定可以了解葡萄酒是否生病、病害的严重性以及预测贮藏的困难程度。在国标中对挥发酸和柠檬酸做了明确规定。


-
PH值是衡量葡萄酒中酸度的程度,一般来说,白葡萄酒的酸度一般在3.1至3.5之间,高于红葡萄酒的3.5至4的区间值。相较而言酸度是衡量葡萄酒中酸含量的多少。
-
一般来说,酸度对葡萄酒口感的影响要大于PH值,但如果PH值位于一个极端的位置,就会产生较大的影响。总酸度是告诉我们这款酒的浓度,而PH值显示的是这款酒品尝起来口感的浓郁度。例如,在PH值相同的情况下,一款总酸度为6g/L的葡萄酒品尝起来会比总酸度为4g/L的葡萄酒更酸。
-
残留糖分(简称残糖)是衡量葡萄酒中甜度的标准。通常,残留糖分低于4克/升的葡萄酒为干型葡萄酒,许多干型葡萄酒几乎不含残糖。

-
酒精度指葡萄酒中所含酒精的百分比,大部分葡萄酒的酒精度都在10-15%之间,但也有些特殊的葡萄酒,如阿斯蒂(Moscato d’Asti)(酒精度非常低),波特酒(Port)(酒精度非常高)。

-
氯化物和硫酸盐都属于葡萄酒中的矿物盐成分,一般来说含量分别是0.1-0.4g/L和0.25-0.85g/L。值得一提的是,虽然这些矿物质成分存在葡萄酒中且可以增强葡萄酒的风味,但它们并不是某些葡萄酒带有矿物风味的主要原因。一般而言,红葡萄酒所含的矿物质多于白葡萄酒。
-
并不是所有葡萄酒中都会有二氧化硫,但二氧化硫能起到如杀菌、抗氧化、澄清酒液和提高色素和酚类物质含量等作用,因此一般葡萄酒中或多或少地带有一定的二氧化硫,只是整体而言其含量非常少,多为 80-200mg/L,个别葡萄酒中还含有 10-50mg/L 的游离态二氧化硫。不过,适当的摇杯或者醒酒等可以令其挥发掉,因此几乎可以忽略不计。

在欧盟,干红葡萄酒中二氧化硫的最高含量为 160mg/L,白葡萄酒和桃红葡萄酒为 210mg/L,甜型葡萄酒中的二氧化硫含量可能更高。
根据查到的信息,更新输入变量表格如下:
| 输入指标 | 说明 | 备注 |
|---|---|---|
| fixed acidity | 固定酸(g/L) | 总酸组成之一 |
| volatile acidity | 挥发性酸(g/L) | 总酸组成之一 |
| citric acid | 柠檬酸(g/L) | 属于固定酸 |
| residual sugar | 残留糖(g/L) | 基本指标之一 |
| chlorides | 氯化物(g/L) | 矿物盐成分 |
| free sulfur dioxide | 游离二氧化硫(mg/L) | 防腐保鲜剂 |
| total sulfur dioxide | 二氧化硫总量(mg/L) | 防腐保鲜剂 |
| density | 密度(g/ml) | 略 |
| pH | 酸碱值 | 酸度的另一种测量角度 |
| sulphates | 硫酸盐(g/L) | 矿物盐成分 |
| alcohol | 酒精 (%vol) | 基本指标之一 |
由此可知,11种输入变量可以大致划分成三类,第一类是基本指标及其内含的个别具体指标,第二类是附加指标(矿物盐、二氧化硫),第三类是密度这个物理性质。
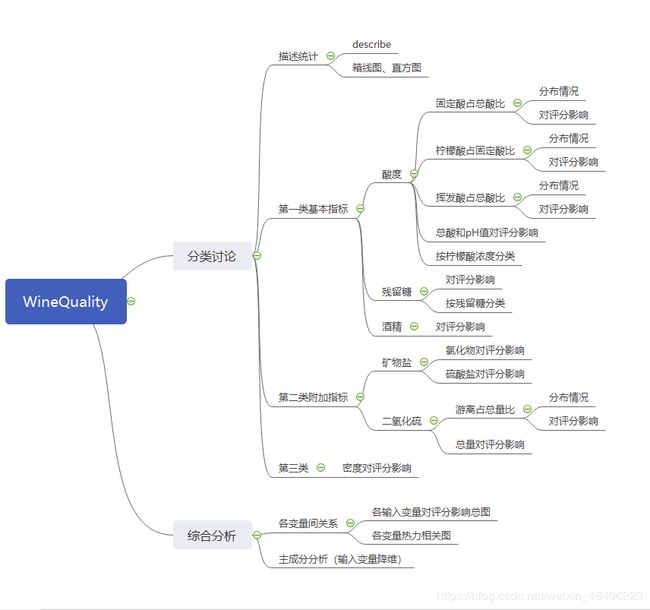
根据以上信息,拟定分析内容如下图所示:
二、数据分析(Python)
0.数据清洗
使用Jupyter Notebook进行代码工作,首先加载需要用到的库:
%matplotlib inline
#%config InlineBackend.figure_format = 'retina'
import numpy as np
import pandas as pd
import matplotlib.pyplot as plt
import seaborn as sns
# 颜色
color = sns.color_palette()
# 数据print精度
pd.set_option('precision',3)
这里开局就报错了,good。问题出在seaborn这个库,解决过程详见:Python seaborn库导入报错的解决,简而言之就是在anaconda中创建一个虚拟环境,安装python3.6的环境,再安装这几个库。
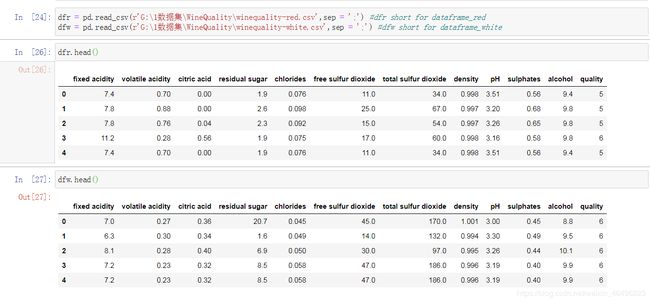
安装完毕后,重新输入上述代码,运行完毕。然后读取文件:
dfr = pd.read_csv(r'G:\1数据集\WineQuality\winequality-red.csv',sep = ';') #dfr short for dataframe_red
dfw = pd.read_csv(r'G:\1数据集\WineQuality\winequality-white.csv',sep = ';') #dfw short for dataframe_white
结果如下:
因为总酸作为葡萄酒基本指标值之一,是固定酸和挥发酸的合,所以可以在表中增加一列"total acid"作为总酸,并放置在表格首列:
#增加总酸
dfr['total acid'] = dfr['fixed acidity'] + dfr['volatile acidity']
dfw['total acid'] = dfw['fixed acidity'] + dfw['volatile acidity']
#移动dfr总酸到列首
r = dfr.columns.tolist()
r.insert(0,r.pop())
dfr = dfr.reindex(columns=r)
#移动dfw总酸到列首
r = dfw.columns.tolist()
r.insert(0,r.pop())
dfw = dfw.reindex(columns=r)
因为不存在值必须唯一的变量且需要分析分类数量,故此处不对数据集进行去重(经试验两个数据集都存在一定数量的重复值)。
经检查不存在异常值。
至此分析用的数据准备就算完成了。
1.分类讨论
11种输入变量可以大致划分成三类,第一类是基本指标及其内含的个别具体指标,第二类是附加指标(矿物盐、二氧化硫),第三类是密度这个物理性质。
1-1 描述统计
1-1-1 数值描述
首先对两种葡萄酒作描述统计,这个可以.describe()方法直接得到结果
dfr.describe()
dfw.describe()
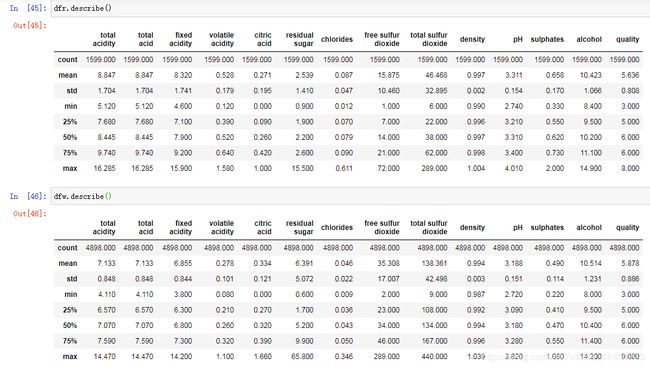
由上面结果首先可以知道参与测试的红葡萄酒获得的评分分布在3-8分,白葡萄酒在3-9分,且各分位数数据一致,这说明两种葡萄酒的品质在大体上无明显区别,但具体是否存在细节上的差距还需要进一步分析。另外对于输入变量的各参数,数据表格展示的形式太繁杂不直观,一时看不出什么信息,需要进一步加工成图像便于分析比对。
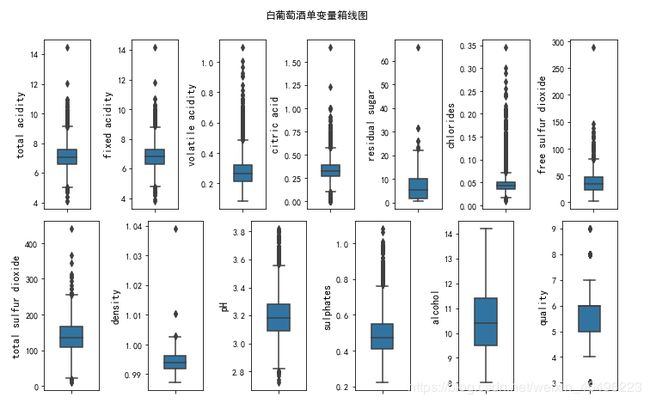
1-1-2 箱线图
进一步,绘制两种葡萄酒每个变量的箱线图
#红葡单变量箱线图
colnm = dfr.columns.tolist()
plt.figure(figsize = (10, 6))
plt.suptitle('红葡萄酒单变量箱线图', y=1.05) #总标题
"""画第一行的图"""
for i in range(7):
plt.subplot(2,7,i+1)
sns.boxplot(dfr[colnm[i]], orient="v", width = 0.4, color = color[0])
plt.ylabel(colnm[i],fontsize = 12)
plt.tight_layout()
"""画第二行的图"""
for i in range(6):
plt.subplot(2,6,i+7)
sns.boxplot(dfr[colnm[i+7]], orient="v", width = 0.4, color = color[0])
plt.ylabel(colnm[i+7],fontsize = 12)
plt.tight_layout()

结合箱线图和刚才的数据表格可以直观了解到各个变量的分布特征,大致归纳如下
| 红葡萄酒变量 | 分布特征 |
|---|---|
| total acidity | 整体呈正偏,尾长较为对称,高浓度部分存在一定量离群点 |
| fixed acidity | 整体呈正偏,尾长较为对称,高浓度部分存在一定量离群点,整体分布与总酸相近 |
| volatile acidity | 整体呈正偏,尾长较为对称,高浓度部分存在一定量离群点,浓度范围低总酸一个数量级 |
| citric acid | 整体呈正偏,上尾长较长,最小值取到0,有极个别离群点取到1 |
| residual sugar | 整体呈高度正偏,尾长较为对称,存在大量高浓度离群点 |
| chlorides | 整体呈高度正偏,尾长较为对称,存在少量低浓度离群点和大量高浓度离群点 |
| free sulfur dioxide | 整体呈正偏,上尾长较长,存在一定量高浓度离群点 |
| total sulfur dioxide | 整体呈正偏,上尾长较长,存在一定量高浓度离群点且离群点间断大 |
| density | 整体几乎呈正态分布,上下各有一定量离群点 |
| pH | 整体呈轻度正偏,尾长较为对称,存在少量低值离群点和一定量高值离群点 |
| sulphates | 整体呈正偏,尾长较为对称,存在较多高浓度离群点 |
| alcohol | 整体呈正偏,上尾长较长,存在少量高浓度离群点 |
| quality | 整体几乎呈正太分布,上下各有极少量离群点 |
可以大致总结知道,对于红葡萄酒而言,除密度和评分这两项数据分布均匀呈正态之外,其他所有变量都呈现出不同程度的正偏分布,这说明大多数变量都存在可控下限却没有明确的上限,由于品质波动都可能出现较高取值的情况。
#白葡单变量箱线图
colnm = dfw.columns.tolist()
plt.figure(figsize = (10, 6))
plt.suptitle('白葡萄酒单变量箱线图', y=1.05) #总标题
"""画第一行的图"""
for i in range(7):
plt.subplot(2,7,i+1)
sns.boxplot(dfw[colnm[i]], orient="v", width = 0.4, color = color[0])
plt.ylabel(colnm[i],fontsize = 12)
plt.tight_layout()
"""画第二行的图"""
for i in range(6):
plt.subplot(2,6,i+7)
sns.boxplot(dfw[colnm[i+7]], orient="v", width = 0.4, color = color[0])
plt.ylabel(colnm[i+7],fontsize = 12)
plt.tight_layout()
| 白葡萄酒变量 | 分布特征 |
|---|---|
| total acidity | 整体呈正偏,尾长较为对称,存在少量低离群点和一定量高离群点 |
| fixed acidity | 整体呈正偏,尾长较为对称,存在少量低离群点和一定量高离群点,整体分布与总酸相近 |
| volatile acidity | 整体呈正偏,尾长较为对称,存在大量高离群点,浓度范围低总酸一个数量级 |
| citric acid | 整体呈正偏,尾长较为对称,存在少量低离群点和一定量高离群点 |
| residual sugar | 整体呈正偏,上尾长较长,存在少量高浓度离群点且离群点间断大 |
| chlorides | 整体呈高度正偏,尾长较为对称,存在少量低浓度离群点和大量高浓度离群点 |
| free sulfur dioxide | 整体呈正偏,上尾长较长,存在一定量高浓度离群点且离群点间断大 |
| total sulfur dioxide | 整体呈正偏,尾长较为对称,存在少量低离群点一定量高浓度离群点 |
| density | 整体呈轻度正偏,存在极少量高离群点 |
| pH | 整体呈轻度正偏,尾长较为对称,存在少量低离群点和一定量高离群点 |
| sulphates | 整体呈正偏,尾长较为对称,存在较多高浓度离群点 |
| alcohol | 整体呈正偏,上尾长较长,无离群点 |
| quality | 整体几乎呈正太分布,上下各有极少量离群点 |
可以发现白葡萄酒也是在绝大部分变量上呈现正偏分布,且相比红葡萄酒有更多变量有低离群点,整体上红葡萄酒和白葡萄酒在一些变量上表现不太相同,这些指标可能是造成品类不同的主要因素之一。
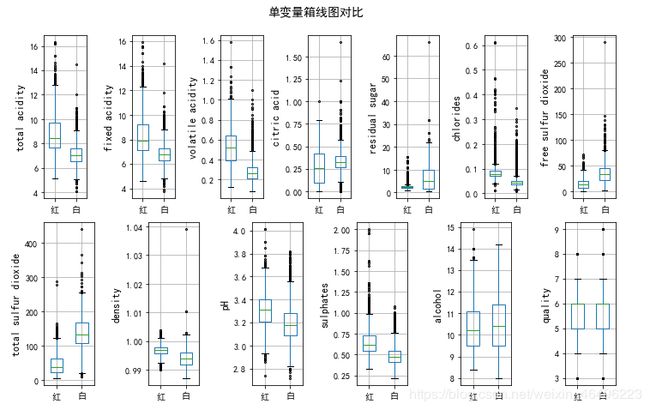
至此已经分别对红、白葡萄酒的情况有了初步了解,那二者之间是否有什么区别呢?可以把两种酒的变量箱线图放在一起进行观察:
#红白变量箱线图
colnm_r = dfr.columns.tolist()
colnm_w = dfw.columns.tolist()
plt.figure(figsize = (10, 6))
plt.suptitle('单变量箱线图对比',fontsize=14, y=1.05) #总标题
"""画第一行的图"""
for i in range(7):
y1 = dfr[colnm_r[i]]
y2 = dfw[colnm_w[i]]
data = pd.DataFrame({"红": y1, "白": y2})
plt.subplot(2,7,i+1)
data.boxplot(widths=0.5,flierprops = {'marker':'o','markersize':2})
plt.ylabel(colnm_r[i],fontsize = 12)
plt.tight_layout()
"""画第二行的图"""
for i in range(6):
y1 = dfr[colnm_r[i+7]]
y2 = dfw[colnm_w[i+7]]
data = pd.DataFrame({"红": y1, "白": y2})
plt.subplot(2,6,i+7)
data.boxplot(widths=0.5,flierprops = {'marker':'o','markersize':2})
plt.ylabel(colnm_r[i+7],fontsize = 12)
plt.tight_layout()
- 在酸度上白葡萄酒取值低于红葡萄酒且分布更紧凑;
- 在残留糖浓度上白葡萄酒分布更广泛,相比之下红葡萄酒的分布就很紧凑;
- 在氯化物浓度上白葡萄酒取值低于红葡萄酒,二者的分布都比较分散;
- 在二氧化硫浓度上白葡萄酒取值高于红葡萄酒;
- 在密度上二者的绝大部分取值均低于水的密度,白葡萄酒整体密度更低但分布范围更大;
- 在pH上二者整体分布相似,白葡萄酒取值整体低于红葡萄酒;
- 在硫酸盐酸浓度上白葡萄酒整体取值低于红葡萄酒;
- 在酒精浓度上二者分布相近且离群点很少;
- 在品质评分上二者十分相近,除白葡萄酒有9分取值外几乎无异;
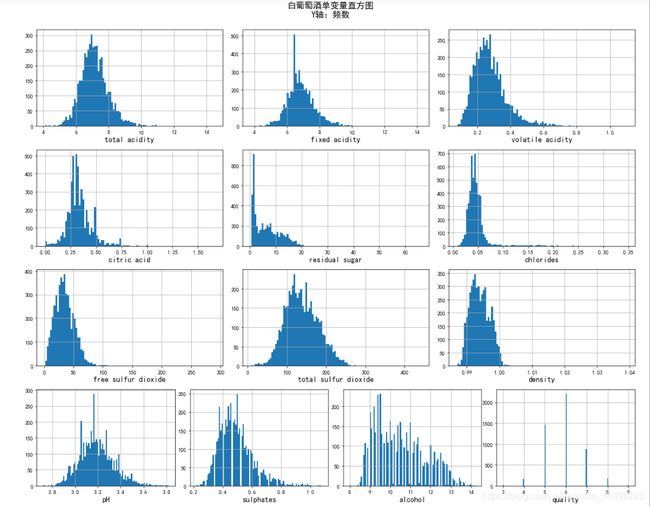
1-1-3 直方图
除了箱线图,还可以通过直方图从另一种角度观察每种变量的分布情况。作为对比参考,分析上不做赘述
绘制每个变量的直方图
#红葡单变量直方图
colnm = dfr.columns.tolist()
plt.figure(figsize = (16, 12))
plt.suptitle('红葡萄酒单变量直方图\nY轴:频数', y=1.05, fontsize = 16) #总标题
"""画前三行的图"""
for i in range(9):
plt.subplot(4,3,i+1)
dfr[colnm[i]].hist(bins = 100, color = color[0])
plt.xlabel(colnm[i],fontsize = 14)
plt.tight_layout()
"""画第四行的图"""
for i in range(4):
plt.subplot(4,4,i+13)
dfr[colnm[i+9]].hist(bins = 100, color = color[0])
plt.xlabel(colnm[i+9],fontsize = 14)
plt.tight_layout()
#白葡单变量直方图
colnm = dfw.columns.tolist()
plt.figure(figsize = (16, 12))
plt.suptitle('白葡萄酒单变量直方图\nY轴:频数', y=1.05, fontsize = 16) #总标题
"""画前三行的图"""
for i in range(9):
plt.subplot(4,3,i+1)
dfw[colnm[i]].hist(bins = 100, color = color[0])
plt.xlabel(colnm[i],fontsize = 14)
plt.tight_layout()
"""画第四行的图"""
for i in range(4):
plt.subplot(4,4,i+13)
dfw[colnm[i+9]].hist(bins = 100, color = color[0])
plt.xlabel(colnm[i+9],fontsize = 14)
plt.tight_layout()
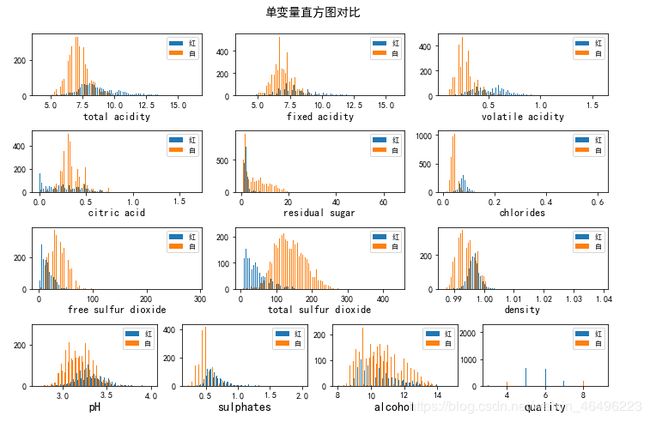
当然,也可以将两种葡萄酒的变量直方图放在一张图上进行更为直观的对比分析,结果如下:
#红白变量箱线图
colnm_r = dfr.columns.tolist()
colnm_w = dfw.columns.tolist()
plt.figure(figsize = (10, 6))
plt.suptitle('单变量直方图对比',fontsize=14, y=1.05) #总标题
"""画前三行的图"""
for i in range(9):
y1 = dfr[colnm_r[i]].tolist()
y2 = dfw[colnm_w[i]].tolist()
data = []
data.append(y1)
data.append(y2)
plt.subplot(4,3,i+1)
plt.hist(data, bins=100, histtype='bar')
plt.legend(['红','白'],prop={'size': 8})
plt.xlabel(colnm_r[i],fontsize = 12)
plt.tight_layout()
"""画第四行的图"""
for i in range(4):
y1 = dfr[colnm_r[i+9]].tolist()
y2 = dfw[colnm_w[i+9]].tolist()
data = []
data.append(y1)
data.append(y2)
plt.subplot(4,4,i+13)
plt.hist(data, bins=100, histtype='bar')
plt.legend(['红','白'],prop={'size': 8})
plt.xlabel(colnm_r[i+9],fontsize = 14)
plt.tight_layout()
1-2 第一类(基本指标)
1-2-1 酸度
1-2-1-1、输入变量中有很多跟酸相关的变量,需逐个对其进行分析。首先是固定酸在总酸中的占比,观察占比的分布情况。
#固定酸占总酸比重
plt.figure(figsize = (10,4))
plt.suptitle('固定酸占总酸比分布情况', y=1.02, fontsize = 16) #总标题
"""红"""
plt.subplot(1,2,1)
temp = dfr[{'total acidity','fixed acidity'}]
temp['precent'] = temp.apply(lambda x: x['fixed acidity']/x['total acidity'], axis=1) #计算占比
temp['precent'].hist(bins = 100, color = color[0])
plt.xlabel('红葡萄酒固定酸占比',fontsize = 12)
plt.ylabel('频数',fontsize = 12)
"""白"""
plt.subplot(1,2,2)
temp = dfw[{'total acidity','fixed acidity'}]
temp['precent'] = temp.apply(lambda x: x['fixed acidity']/x['total acidity'], axis=1) #计算占比
temp['precent'].hist(bins = 100, color = color[0])
plt.xlabel('白葡萄酒固定酸占比',fontsize = 12)
plt.ylabel('频数',fontsize = 12)

可以发现红葡萄酒中固定酸的占比比较分散,而白葡萄酒中固定酸的占比则比较集中,形成一个单峰分布。两种葡萄酒的固定酸占比大多数情况下都达到了90%以上。
其次是关于固定酸占总酸比重对评分的影响
#固定酸占比对评分影响
plt.figure(figsize = (10,4))
plt.suptitle('固定酸占总酸比对评分的影响', y=1.02, fontsize = 16) #总标题
"""红"""
plt.subplot(1,2,1)
temp = dfr[{'total acidity','fixed acidity','quality'}]
temp['precent'] = temp.apply(lambda x: x['fixed acidity']/x['total acidity'], axis=1) #计算占比
sns.boxplot(x=temp['quality'], y=temp['precent'])
plt.xlabel('红葡萄酒评分',fontsize = 12)
plt.ylabel('固定酸占比',fontsize = 12)
"""白"""
plt.subplot(1,2,2)
temp = dfw[{'total acidity','fixed acidity','quality'}]
temp['precent'] = temp.apply(lambda x: x['fixed acidity']/x['total acidity'], axis=1) #计算占比
sns.boxplot(x=temp['quality'], y=temp['precent'])
plt.xlabel('白葡萄酒评分',fontsize = 12)
plt.ylabel('固定酸占比',fontsize = 12)
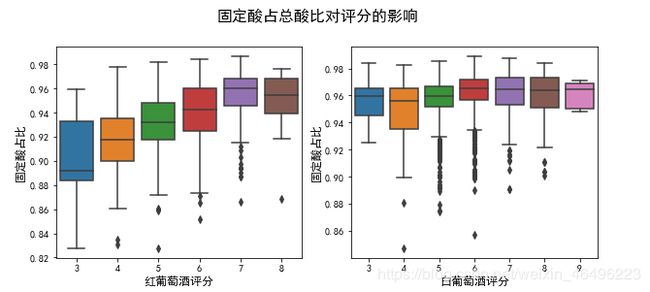
可以发现随着占比的提高,红葡萄酒有更大可能取得较高的评分,而占比的提高对白葡萄酒影响不显著。
1-2-1-2、柠檬酸是固定酸的一种,若观察固定酸和柠檬酸的关系,首先可以观察柠檬酸在固定酸中占比的分布情况。
#柠檬酸占固定酸比重
plt.figure(figsize = (10,4))
plt.suptitle('柠檬酸占固定酸比分布情况', y=1.02, fontsize = 16) #总标题
"""红"""
plt.subplot(1,2,1)
temp = dfr[{'citric acid','fixed acidity'}]
temp['precent'] = temp.apply(lambda x: x['citric acid']/x['fixed acidity'], axis=1) #计算占比
temp['precent'].hist(bins = 100, color = color[0])
plt.xlabel('红葡萄酒柠檬酸占比',fontsize = 12)
plt.ylabel('频数',fontsize = 12)
"""白"""
plt.subplot(1,2,2)
temp = dfw[{'citric acid','fixed acidity'}]
temp['precent'] = temp.apply(lambda x: x['citric acid']/x['fixed acidity'], axis=1) #计算占比
temp['precent'].hist(bins = 100, color = color[0])
plt.xlabel('白葡萄酒柠檬酸占比',fontsize = 12)
plt.ylabel('频数',fontsize = 12)
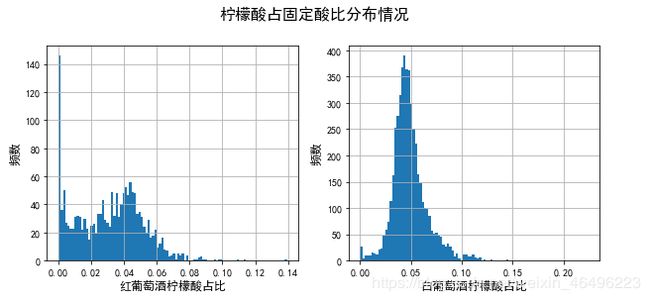
可以发现,柠檬酸的占比在红葡萄酒中比较分散,大部分分布于0-8%,且有大量0值。白葡萄酒中柠檬酸占比呈明显的单峰分布,大概集中于4.5%附近。
其次是关于柠檬酸占固定酸比重对评分的影响
#柠檬酸占比对评分影响
plt.figure(figsize = (10,4))
plt.suptitle('柠檬酸占固定酸比对评分的影响', y=1.02, fontsize = 16) #总标题
"""红"""
plt.subplot(1,2,1)
temp = dfr[{'citric acid','fixed acidity','quality'}]
temp['precent'] = temp.apply(lambda x: x['citric acid']/x['fixed acidity'], axis=1) #计算占比
sns.boxplot(x=temp['quality'], y=temp['precent'])
plt.xlabel('红葡萄酒评分',fontsize = 12)
plt.ylabel('柠檬酸占比',fontsize = 12)
"""白"""
plt.subplot(1,2,2)
temp = dfw[{'citric acid','fixed acidity','quality'}]
temp['precent'] = temp.apply(lambda x: x['citric acid']/x['fixed acidity'], axis=1) #计算占比
sns.boxplot(x=temp['quality'], y=temp['precent'])
plt.xlabel('白葡萄酒评分',fontsize = 12)
plt.ylabel('柠檬酸占比',fontsize = 12)

可以发现随着柠檬酸占比的提高,红葡萄酒有更大可能取得较高的评分。而占比的提高对白葡萄酒影响不显著,但过高的占比会导致评分处于中间分段。
1-2-1-3、因为挥发酸是不良指标,所以挥发酸含量对评分的影响应该能形成规律。首先观察挥发酸在总酸中的占比的分布情况
#挥发酸占总酸比重
plt.figure(figsize = (10,4))
plt.suptitle('挥发酸占总酸比分布情况', y=1.02, fontsize = 16) #总标题
"""红"""
plt.subplot(1,2,1)
temp = dfr[{'total acidity','volatile acidity'}]
temp['precent'] = temp.apply(lambda x: x['volatile acidity']/x['total acidity'], axis=1) #计算占比
temp['precent'].hist(bins = 100, color = color[0])
plt.xlabel('红葡萄酒挥发酸占比',fontsize = 12)
plt.ylabel('频数',fontsize = 12)
"""白"""
plt.subplot(1,2,2)
temp = dfw[{'total acidity','volatile acidity'}]
temp['precent'] = temp.apply(lambda x: x['volatile acidity']/x['total acidity'], axis=1) #计算占比
temp['precent'].hist(bins = 100, color = color[0])
plt.xlabel('白葡萄酒挥发酸占比',fontsize = 12)
plt.ylabel('频数',fontsize = 12)
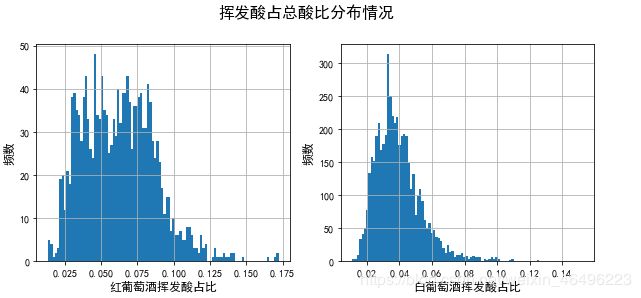
可以发现红葡萄酒中挥发酸的占比比较分散,大部分分布在2.5%-10%之间。而白葡萄酒中固定酸的占比则比较集中,形成一个单峰分布,大概集中在3%附近。
其次是关于挥发酸在总酸中的占比对评分的影响
#挥发酸占比对评分影响
plt.figure(figsize = (10,4))
plt.suptitle('挥发酸占总酸比对评分的影响', y=1.02, fontsize = 16) #总标题
"""红"""
plt.subplot(1,2,1)
temp = dfr[{'total acidity','volatile acidity','quality'}]
temp['precent'] = temp.apply(lambda x: x['volatile acidity']/x['total acidity'], axis=1) #计算占比
sns.boxplot(x=temp['quality'], y=temp['precent'])
plt.xlabel('红葡萄酒评分',fontsize = 12)
plt.ylabel('挥发酸占比',fontsize = 12)
"""白"""
plt.subplot(1,2,2)
temp = dfw[{'total acidity','volatile acidity','quality'}]
temp['precent'] = temp.apply(lambda x: x['volatile acidity']/x['total acidity'], axis=1) #计算占比
sns.boxplot(x=temp['quality'], y=temp['precent'])
plt.xlabel('白葡萄酒评分',fontsize = 12)
plt.ylabel('挥发酸占比',fontsize = 12)

可以发现随着挥发酸占比降低,红葡萄酒有更大可能取得较高得分,而占比的降低对白葡萄酒的影响不显著。
1-2-1-4、酸度和pH都是对酸性的度量,只是角度不同,需观察二者对评分结果的影响力是否有差距。
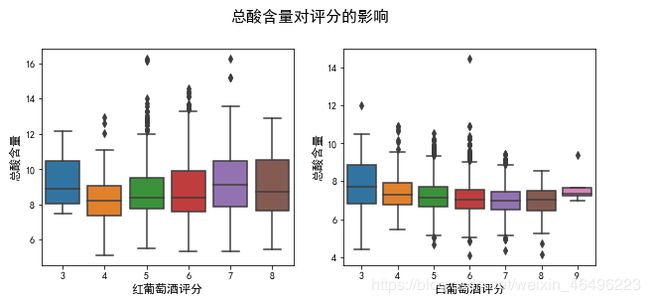
首先是总酸对评分的影响。
#总酸对评分影响
plt.figure(figsize = (10,4))
plt.suptitle('总酸含量对评分的影响', y=1.02, fontsize = 16) #总标题
"""红"""
plt.subplot(1,2,1)
temp = dfr[{'total acidity','quality'}]
sns.boxplot(x=temp['quality'], y=temp['total acidity'])
plt.xlabel('红葡萄酒评分',fontsize = 12)
plt.ylabel('总酸含量',fontsize = 12)
"""白"""
plt.subplot(1,2,2)
temp = dfw[{'total acidity','quality'}]
sns.boxplot(x=temp['quality'], y=temp['total acidity'])
plt.xlabel('白葡萄酒评分',fontsize = 12)
plt.ylabel('总酸含量',fontsize = 12)
#pH对评分影响
plt.figure(figsize = (10,4))
plt.suptitle('pH值对评分的影响', y=1.02, fontsize = 16) #总标题
"""红"""
plt.subplot(1,2,1)
temp = dfr[{'pH','quality'}]
sns.boxplot(x=temp['quality'], y=temp['pH'])
plt.xlabel('红葡萄酒评分',fontsize = 12)
plt.ylabel('pH值',fontsize = 12)
"""白"""
plt.subplot(1,2,2)
temp = dfw[{'pH','quality'}]
sns.boxplot(x=temp['quality'], y=temp['pH'])
plt.xlabel('白葡萄酒评分',fontsize = 12)
plt.ylabel('pH值',fontsize = 12)
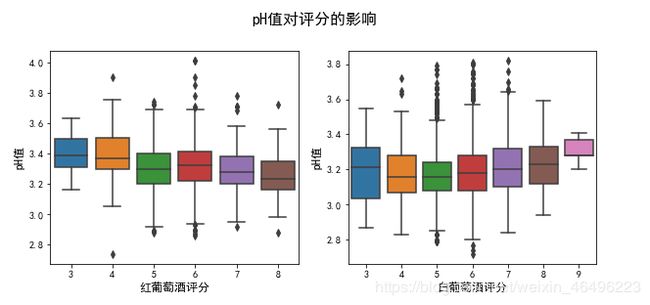
可以发现,总酸含量的变化对红白葡萄酒均没有显著的影响,而pH值的降低会使红葡萄酒有更大可能获得高分评价,使白葡萄酒有更大可能获得低分评价。pH值对两种葡萄酒的影响是恰好相反的。
1-2-1-8、国标中有根据柠檬酸的浓度对葡萄酒分类的标准,此处按这个标椎看一下分类结果

#按柠檬酸分类
plt.figure(figsize = (10,4))
plt.suptitle('按柠檬酸含量分类', y=1.02, fontsize = 16) #总标题
"""红"""
plt.subplot(1,2,1)
temp = pd.cut(dfr['citric acid'], bins=[-0.1, 1, 2], labels=["干、半干、半甜", "甜"])
temp = pd.DataFrame(temp)
temp['citric acid'].value_counts().plot(kind='bar')
num = temp['citric acid'].value_counts()
for x, y in enumerate(num.values):
plt.text(x, y, "%s" %y, ha='center', va='bottom') #显示数字
plt.xticks(rotation=360)
"""白"""
plt.subplot(1,2,2)
temp = pd.cut(dfw['citric acid'], bins=[-0.1, 1, 2.1], labels=["干、半干、半甜", "甜"])
temp = pd.DataFrame(temp)
temp['citric acid'].value_counts().plot(kind='bar')
num = temp['citric acid'].value_counts()
for x, y in enumerate(num.values):
plt.text(x, y, "%s" %y, ha='center', va='bottom') #显示数字
plt.xticks(rotation=360)
按照国标,实验中所有的红葡萄酒都属于(干、半干、半甜)类,没有甜葡萄酒。
实验中99%的白葡萄酒都属于(干、半干、半甜)类,只有2例甜葡萄酒。
1-2-2 残留糖
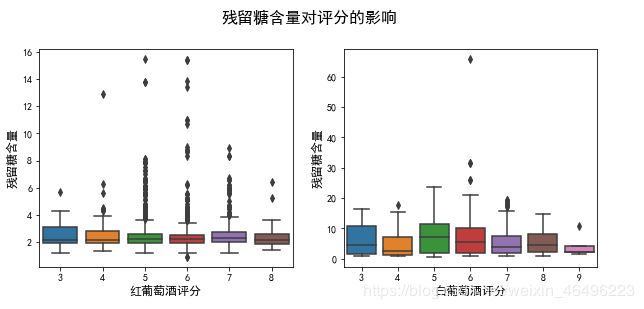
1-2-2-1、作为基本指标之一,先观察残留糖对评分的影响
#残留糖对评分影响
plt.figure(figsize = (10,4))
plt.suptitle('残留糖含量对评分的影响', y=1.02, fontsize = 16) #总标题
"""红"""
plt.subplot(1,2,1)
sns.boxplot(x=dfr['quality'], y=dfr['residual sugar'])
plt.xlabel('红葡萄酒评分',fontsize = 12)
plt.ylabel('残留糖含量',fontsize = 12)
"""白"""
plt.subplot(1,2,2)
sns.boxplot(x=dfw['quality'], y=dfw['residual sugar'])
plt.xlabel('白葡萄酒评分',fontsize = 12)
plt.ylabel('残留糖含量',fontsize = 12)
除去离群点,各分段的红葡萄酒的残留糖含量都比较相近,可以认为残留糖含量对红葡萄酒的评分影响不大。可以观察到8分红葡和3分红葡的残留糖含量分布区间很相近,而高浓度离群点主要出现在中间分段,不见于高分段和低分段。
类似地,除去离群点,各分段的白葡萄酒的残留糖含量都比较相近,可以认为残留糖含量对白葡萄酒的评分影响不大。可以观察到9分白葡和3分白葡的残留糖含量分布区间很相近,而高浓度离群点主要出现在中间分段,不见于高分段和低分段。
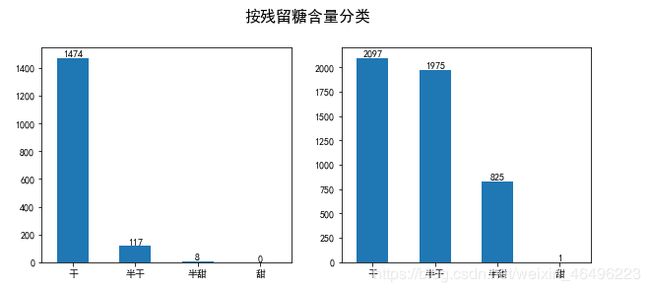
1-2-2-2、国标中有根据糖分的浓度对葡萄酒分类的标准,此处虽不严格复合(应以葡萄糖计),但也可按这个标椎大致看一下分类结果

#按残留糖含量分类
plt.figure(figsize = (10,4))
plt.suptitle('按残留糖含量分类', y=1.02, fontsize = 16) #总标题
"""红"""
plt.subplot(1,2,1)
temp = pd.cut(dfr['residual sugar'], bins=[-0.1, 4, 12, 45,100], labels=["干", "半干", "半甜", "甜"])
temp = pd.DataFrame(temp)
temp['residual sugar'].value_counts().plot(kind='bar')
num = temp['residual sugar'].value_counts()
for x, y in enumerate(num.values):
plt.text(x, y, "%s" %y, ha='center', va='bottom')
plt.xticks(rotation=360)
"""白"""
plt.subplot(1,2,2)
temp = pd.cut(dfw['residual sugar'], bins=[-0.1, 4, 12, 45,100], labels=["干", "半干", "半甜", "甜"])
temp = pd.DataFrame(temp)
temp['residual sugar'].value_counts().plot(kind='bar')
num = temp['residual sugar'].value_counts()
for x, y in enumerate(num.values):
plt.text(x, y, "%s" %y, ha='center', va='bottom')
plt.xticks(rotation=360)
按照国标,实验中干红葡萄酒有1474例,占92.2%,半干红葡萄酒有117例,占7.3%,半甜红葡萄酒有8例,占0.5%,无甜红葡萄酒
实验中干白葡萄酒有2097例,占42.82%,半干白葡萄酒有1975例,占40.32%,半甜白葡萄酒有825例,占16.84%,甜白葡萄酒1例,占0.02%
1-2-3 酒精
1-2-3-1、酒精浓度对评分的影响
#酒精浓度对评分影响
plt.figure(figsize = (10,4))
plt.suptitle('酒精浓度对评分的影响', y=1.02, fontsize = 16) #总标题
"""红"""
plt.subplot(1,2,1)
sns.boxplot(x=dfr['quality'], y=dfr['alcohol'])
plt.xlabel('红葡萄酒评分',fontsize = 12)
plt.ylabel('酒精浓度',fontsize = 12)
"""白"""
plt.subplot(1,2,2)
sns.boxplot(x=dfw['quality'], y=dfw['alcohol'])
plt.xlabel('白葡萄酒评分',fontsize = 12)
plt.ylabel('酒精浓度',fontsize = 12)
可以发现,对于红白葡萄酒而言,酒精浓度的上升会带来一定的评分上涨趋势,较高的酒精浓度更有可能带来较高的评分。
1-2-3-2、按国标标准,葡萄酒酒精浓度应不低于7.0,此处按这个标椎做一下检查,可见均没有不符标准的情况。
(dfr[dfr['alcohol'] < 7]).alcohol.count()
(dfw[dfw['alcohol'] < 7]).alcohol.count()
1-3 第二类(附加指标)
1-3-1 矿物盐
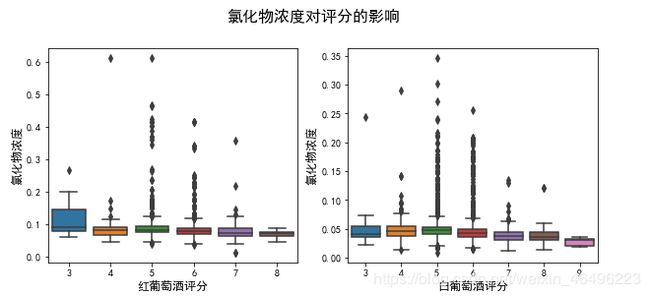
1-3-1-1、氯化物含量对评分的影响
#氯化物浓度对评分影响
plt.figure(figsize = (10,4))
plt.suptitle('氯化物浓度对评分的影响', y=1.02, fontsize = 16) #总标题
"""红"""
plt.subplot(1,2,1)
sns.boxplot(x=dfr['quality'], y=dfr['chlorides'])
plt.xlabel('红葡萄酒评分',fontsize = 12)
plt.ylabel('氯化物浓度',fontsize = 12)
"""白"""
plt.subplot(1,2,2)
sns.boxplot(x=dfw['quality'], y=dfw['chlorides'])
plt.xlabel('白葡萄酒评分',fontsize = 12)
plt.ylabel('氯化物浓度',fontsize = 12)
可以发现有一个微弱的随浓度降低评分上升的趋势,总体来说还是不算显著。但若出现较高浓度,则很有可能该评分处于中间分段。
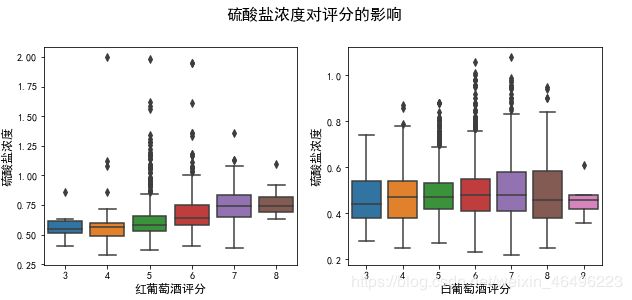
1-3-1-2、硫酸盐含量对评分的影响
#硫酸盐浓度对评分影响
plt.figure(figsize = (10,4))
plt.suptitle('硫酸盐浓度对评分的影响', y=1.02, fontsize = 16) #总标题
"""红"""
plt.subplot(1,2,1)
sns.boxplot(x=dfr['quality'], y=dfr['sulphates'])
plt.xlabel('红葡萄酒评分',fontsize = 12)
plt.ylabel('硫酸盐浓度',fontsize = 12)
"""白"""
plt.subplot(1,2,2)
sns.boxplot(x=dfw['quality'], y=dfw['sulphates'])
plt.xlabel('白葡萄酒评分',fontsize = 12)
plt.ylabel('硫酸盐浓度',fontsize = 12)
可以发现硫酸盐浓度对红葡萄酒的评分有一个较明显影响趋势,随着浓度增加更有可能得到一个较高的评分。
可以发现不能从硫酸盐浓度有效的估计白葡萄酒的评分。但若出现较高浓度,则很有可能该评分处于中间分段。
1-3-2 二氧化硫
1-3-2-1、游离态二氧化硫占二氧化硫总量的比重对评分的影响
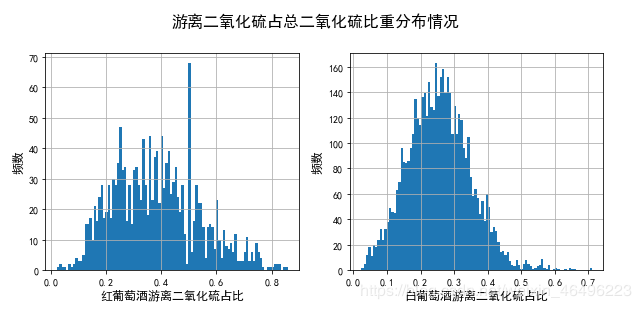
#游离二氧化硫占总二氧化硫比重
plt.figure(figsize = (10,4))
plt.suptitle('游离二氧化硫占总二氧化硫比重分布情况', y=1.02, fontsize = 16) #总标题
"""红"""
plt.subplot(1,2,1)
temp = dfr[{'free sulfur dioxide','total sulfur dioxide'}]
temp['precent'] = temp.apply(lambda x: x['free sulfur dioxide']/x['total sulfur dioxide'], axis=1) #计算占比
temp['precent'].hist(bins = 100, color = color[0])
plt.xlabel('红葡萄酒游离二氧化硫占比',fontsize = 12)
plt.ylabel('频数',fontsize = 12)
"""白"""
plt.subplot(1,2,2)
temp = dfw[{'free sulfur dioxide','total sulfur dioxide'}]
temp['precent'] = temp.apply(lambda x: x['free sulfur dioxide']/x['total sulfur dioxide'], axis=1) #计算占比
temp['precent'].hist(bins = 100, color = color[0])
plt.xlabel('白葡萄酒游离二氧化硫占比',fontsize = 12)
plt.ylabel('频数',fontsize = 12)
#游离二氧化硫占比对评分影响
plt.figure(figsize = (10,4))
plt.suptitle('游离二氧化硫占总二氧化硫比重对评分的影响', y=1.02, fontsize = 16) #总标题
"""红"""
plt.subplot(1,2,1)
temp = dfr[{'free sulfur dioxide','total sulfur dioxide','quality'}]
temp['precent'] = temp.apply(lambda x: x['free sulfur dioxide']/x['total sulfur dioxide'], axis=1)
sns.boxplot(x=temp['quality'], y=temp['precent'])
plt.xlabel('红葡萄酒评分',fontsize = 12)
plt.ylabel('游离二氧化硫占比',fontsize = 12)
"""白"""
plt.subplot(1,2,2)
temp = dfw[{'free sulfur dioxide','total sulfur dioxide','quality'}]
temp['precent'] = temp.apply(lambda x: x['free sulfur dioxide']/x['total sulfur dioxide'], axis=1)
sns.boxplot(x=temp['quality'], y=temp['precent'])
plt.xlabel('白葡萄酒评分',fontsize = 12)
plt.ylabel('游离二氧化硫占比',fontsize = 12)
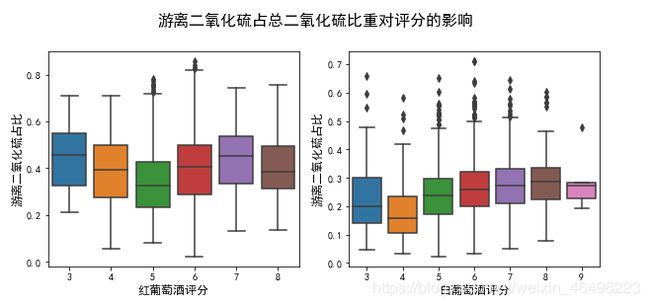
可以发现,仅从游离二氧化硫占总二氧化硫的比重无法有效估计红、白葡萄酒的评分情况。
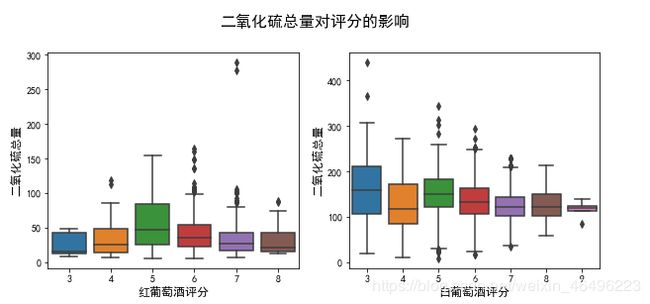
1-3-2-2、二氧化硫总量对评分的影响
#二氧化硫总量对评分影响
plt.figure(figsize = (10,4))
plt.suptitle('二氧化硫总量对评分的影响', y=1.02, fontsize = 16) #总标题
"""红"""
plt.subplot(1,2,1)
sns.boxplot(x=dfr['quality'], y=dfr['total sulfur dioxide'])
plt.xlabel('红葡萄酒评分',fontsize = 12)
plt.ylabel('二氧化硫总量',fontsize = 12)
"""白"""
plt.subplot(1,2,2)
sns.boxplot(x=dfw['quality'], y=dfw['total sulfur dioxide'])
plt.xlabel('白葡萄酒评分',fontsize = 12)
plt.ylabel('二氧化硫总量',fontsize = 12)
可以发现,仅从二氧化硫的总浓度亦无法有效估计红、白葡萄酒的评分情况,不过若出现高浓度二氧化硫,则有更大可能获得中间段评分。
1-4 第三类(密度)
除了之前在描述统计中看到的密度分布情况,这里可以进一步观察密度对评分的影响
#密度对评分影响
plt.figure(figsize = (10,4))
plt.suptitle('密度对评分影响', y=1.02, fontsize = 16) #总标题
"""红"""
plt.subplot(1,2,1)
sns.boxplot(x=dfr['quality'], y=dfr['density'])
plt.xlabel('红葡萄酒评分',fontsize = 12)
plt.ylabel('密度',fontsize = 12)
"""白"""
plt.subplot(1,2,2)
sns.boxplot(x=dfw['quality'], y=dfw['density'])
plt.xlabel('白葡萄酒评分',fontsize = 12)
plt.ylabel('密度',fontsize = 12)

可以发现,对于红葡萄酒而言,随着密度的降低会有一个轻微的取得高分的趋势,而对于白葡萄酒而言,密度的变化并不会影响其评分情况。
2.综合分析
2-1 各变量间关系
2-1-1、评分和各输入变量箱线图
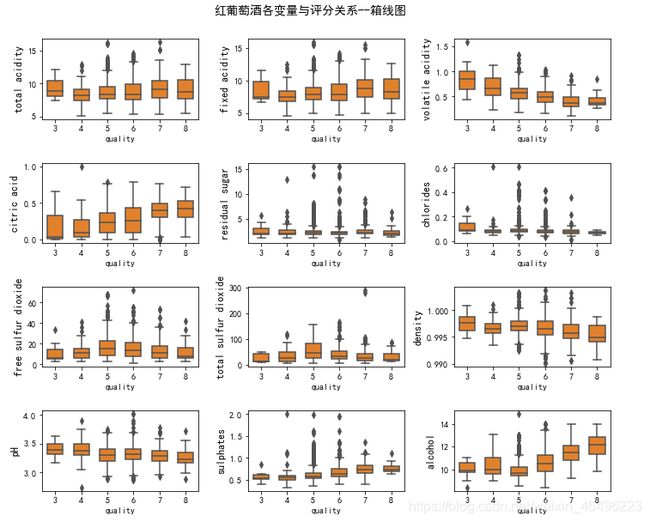
在上一个章节中选择性的查看了大部分输入变量对评分的影响,此处可以进一步将所有输入变量对评分的影响放在一起,类似于总结,可以有一个更加直观的视角。
#红葡各变量与评分关系
colnm = dfr.columns.tolist()[:12]
plt.figure(figsize = (10, 8))
for i in range(12):
plt.subplot(4,3,i+1)
sns.boxplot(x ='quality', y = colnm[i], data = dfr, color = color[1], width = 0.6)
plt.ylabel(colnm[i],fontsize = 12)
plt.suptitle('红葡萄酒各变量与评分关系--箱线图', y=1.05, fontsize=14)
plt.tight_layout()
#白葡各变量与评分关系
colnm = dfw.columns.tolist()[:12]
plt.figure(figsize = (10, 8))
for i in range(12):
plt.subplot(4,3,i+1)
sns.boxplot(x ='quality', y = colnm[i], data = dfw, color = color[1], width = 0.6)
plt.ylabel(colnm[i],fontsize = 12)
plt.suptitle('白葡萄酒各变量与评分关系--箱线图', y=1.05, fontsize=14)
plt.tight_layout()
2-1-2、各变量热力相关图。
#红葡热力相关图
plt.figure(figsize = (10,8))
colnm = dfr.columns.tolist()
mcorr = dfr[colnm].corr()
mask = np.zeros_like(mcorr, dtype=np.bool)
mask[np.triu_indices_from(mask)] = True
cmap = sns.diverging_palette(220, 10, as_cmap=True)
sns.heatmap(mcorr, mask=mask, cmap=cmap, square=True, annot=True, fmt='0.2f')
plt.title('红葡萄酒各变量间热力相关图')

可以发现,就红葡萄酒quality得分与各输入变量的相关关系而言,与之前的读图分析结果基本保持一致,只不过是以数值形式进行了量化,此处不复赘述。
而各输入变量之间,可以发现:
- 总酸与固定酸、柠檬酸、密度有较强正相关,与pH有较强负相关;
- 固定酸与柠檬酸、密度有较强正相关,与pH有较强负相关;
- 挥发酸与柠檬酸有较强负相关;
- 柠檬酸与pH有较强负相关;
- 游离二氧化硫与二氧化硫总量有较强正相关;
- 密度与酒精有较强负相关
各种酸之间的相关、酸与pH的相关以及游离二氧化硫和总二氧化硫的相关关系都易于理解,而密度与酒精浓度的负相关可以进一步作图进行展示:
#红葡密度与酒精
plt.figure(figsize = (6,4))
sns.regplot(x='density', y = 'alcohol', data = dfr, scatter_kws = {'s':10}, color = color[0])
plt.title('红葡萄酒密度与酒精的相关关系')
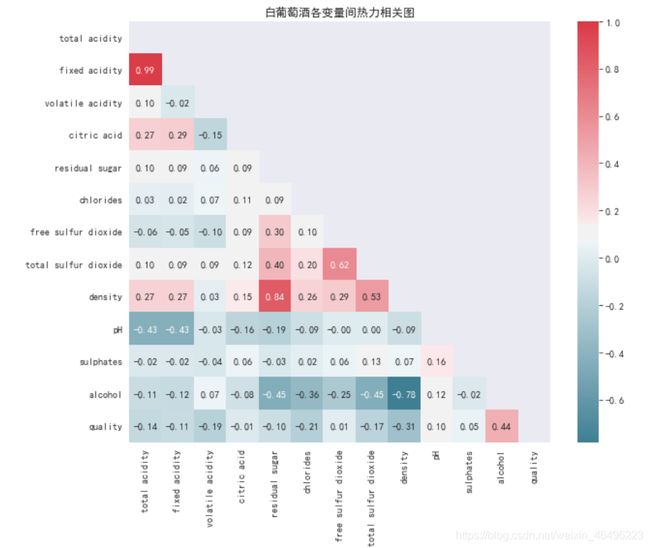
#白葡热力相关图
plt.figure(figsize = (10,8))
colnm = dfw.columns.tolist()
mcorr = dfw[colnm].corr()
mask = np.zeros_like(mcorr, dtype=np.bool)
mask[np.triu_indices_from(mask)] = True
cmap = sns.diverging_palette(220, 10, as_cmap=True)
sns.heatmap(mcorr, mask=mask, cmap=cmap, square=True, annot=True, fmt='0.2f')
plt.title('白葡萄酒各变量间热力相关图')
- 总酸与固定酸有较强正相关,与pH有较弱负相关;
- 固定酸与pH有较弱负相关;
- 残留糖浓度与密度有较强正相关,与酒精浓度有较弱负相关;
- 游离二氧化硫与二氧化硫总量有较强正相关;
- 二氧化硫总量与密度有较强正相关,与酒精有较弱负相关;
- 密度与酒精有较强负相关
可以作图展示一下密度与酒精的负相关和残留糖与酒精的负相关:
#白葡密度与酒精
plt.figure(figsize = (6,4))
sns.regplot(x='density', y = 'alcohol', data = dfw, scatter_kws = {'s':10}, color = color[0])
plt.title('白葡萄酒密度与酒精的相关关系')
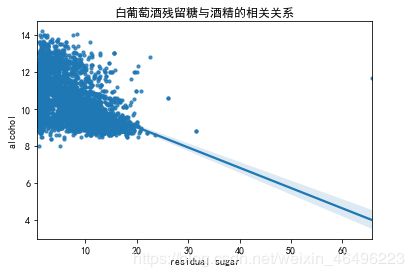
#白葡糖与酒精
plt.figure(figsize = (6,4))
sns.regplot(x='residual sugar', y = 'alcohol', data = dfw, scatter_kws = {'s':10}, color = color[0])
plt.title('白葡萄酒残留糖与酒精的相关关系')
2-2 主成分分析
前述分析中已经知道有些变量之间存在较强相关关系,这表示这些变量指代的含义可能出现重复,即存在浓缩变量的可能。
为验证想法,此处选择运用主成分分析(PCA)对输入变量进行降维,尝试找出具有代表性的少数几个新变量。因为各个变量之间度量单位不同且取值范围差异较大,故选择先将数据进行中心标准化处理,再对标准化的数据求解相关阵(也即协方差阵),进而求解特征值和特征向量。为避免高度重合,在计算之前要先将total acidity和quality这两列剔除出数据。
首先写出主题代码,封装成函数的形式。
#输入变量主成分分析
"""
参数:
- XMat:传入的是一个numpy的矩阵格式,行表示样本数,列表示特征
- k:表示取前k个特征值对应的特征向量
函数解释:
- pca_mat():获取参与运算的多维数组
- pca_eig():返回满足要求的前k个特征值和特征向量
- pca_coe():返回主成分系数
- pca():返回每个样本的主成分得分
- pca_draw():返回前两个主成分得分的散点图
"""
def pca_mat(x):
temp = x.drop(['quality','total acidity'],axis=1) #获取去除评分项的数据表
XMat = np.array(temp) #dataframe格式转为多维数组
average = np.mean(XMat,axis=0) #axis=0表示按照列来求均值
standard = np.std(XMat,axis=0) #求每列标准差
data_adjust = (XMat - average)/standard #中心标准化
return data_adjust
def pca_eig(data_adjust):
covmat = np.cov(data_adjust, rowvar=0) #计算协方差矩阵
eigVals,eigVects = np.linalg.eig(covmat) #求解协方差矩阵的特征值和特征向量
eigValInd = np.argsort(-eigVals) #按照eigVals进行从大到小排序(给出序号,不修改原特征值列表)
"""确定前k的主成分,使选取的主成分贡献90%以上的方差"""
val_sum = 0
val_total = eigVals.sum()
for k in eigValInd:
val_sum += eigVals[k]
if val_sum/val_total < 0.90:
continue
else:
break
"""分割线"""
x = int(np.argwhere(eigValInd==k)+1) #定位k所在位置,结果加1
eigValInd = eigValInd[:x:1] #截取前k个特征值的序号
"""取前k特征值"""
list = []
for i in eigValInd:
list.append(eigVals[i])
redEigVals = np.array(list)
"""对应前k的特征向量"""
redEigVects = []
for i in eigValInd:
redEigVects.append(eigVects[i])
redEigVects = np.array(redEigVects).T
return redEigVals, redEigVects, eigVals, eigVects
def pca_coe(data_adjust):
return pca_eig(data_adjust)[1]/(pca_eig(data_adjust)[0]**0.5)
def pca(data_adjust):
lowDDataMat = np.matrix(data_adjust) * pca_eig(data_adjust)[1]
return lowDDataMat
def pca_draw(data_adjust):
df = pd.DataFrame(pca(data_adjust))
plt.scatter(x=df[0], y=df[1])
if data_adjust.sum() - pca_mat(dfr).sum() == 0:
i = '红葡萄酒'
else:
i = '白葡萄酒'
plt.title(f'{i}'+'主成分得分--散点图')
plt.xlabel('第一主成分', fontsize=12)
plt.ylabel('第二主成分', fontsize=12)
plt.show()
"""红、白葡萄酒初始分析数据"""
pr = pca_mat(dfr)
pw = pca_mat(dfw)
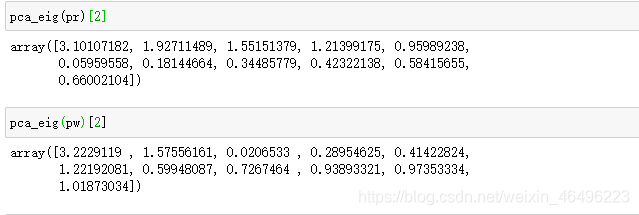
在进行主成分分析的时候,有两点需要注意:
- 变量间不能高度线性相关(故已提前提出明确已知的total acidity),特征值应不要出现十分接近0的情况,若存在则说明变量中存在严重的多重共线性,一定存在某些变量之间高度相关,此时的主成分分析效果将不是很理想。
- 如果各变量之间相关性不大,主成分分析也不会获得理想的效果
对于第一点,经检查可以认为不存在特征值十分接近0的情况:
对于第二点,则需要看看在主成分覆盖90%以上方差的原则下,选取了多少个主成分,若降维效果理想则少数的2-3个主成分即可满足要求。然而如下图所示,在90%标准下,红葡萄酒选出了7个特征值即对应7个主成分,同理白葡萄酒选出了8个主成分,可见两者的主成分降维效果都不是很理想。

结合之前的热力相关图就可以理解,因为大部分变量之间的相关性都很低,具有较强相关的只有少数几个变量,结合上述主成分分析需注意的第二点就知道效果是肯定不会很理想的。
因为效果不理想,其实分析到这里就可以停止了。下面仅作展示将代码执行完成的结果:
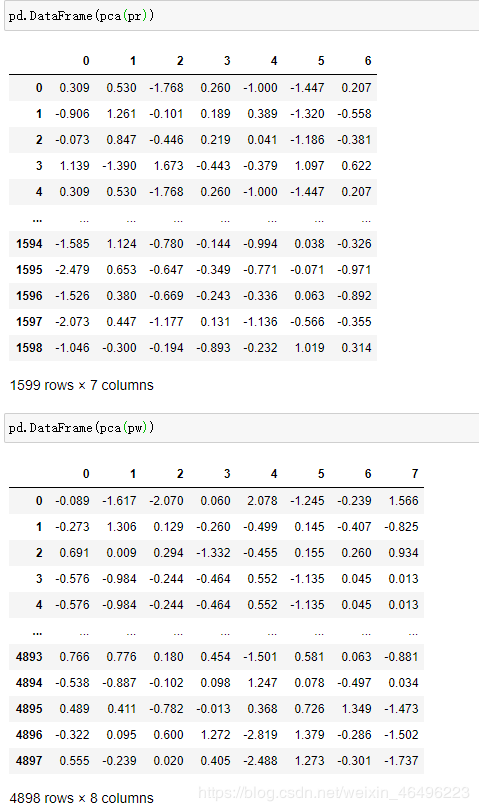
- 主成分系数
解释为第K个主成分表示为11个输入变量的线性组合。可见很难清晰的描述除各主成分代表的含义。
- 主成分得分
解释为每个样本点在主成分上投影的坐标。
3.总结
整体而言,11种输入变量对红葡萄酒的品质评分产生较多的影响,而对白葡萄酒则是在大多情况下无显著趋势,故在此猜测对白葡萄酒评分产生重要影响的另有因素,未在此次实验中被测量。
- 从实验结果来看,红、白葡萄酒的对输入变量的反应可以总结为以下表格
| 变量指标 | 红 | 白 |
|---|---|---|
| 固定酸占总酸比分布情况 | 分布分散,多数>=88% | 单峰分布,集中在97%附近 |
| 固定酸占比对评分影响 | 高占比易得高分 | 无显著趋势 |
| 柠檬酸占固定酸比分布情况 | 分散于0-8%,有很多0值 | 单峰分布,集中在4%附近 |
| 柠檬酸占比对评分影响 | 高占比易得高分 | 无显著趋势 |
| 挥发酸占总酸比分布情况 | 大多数分散于2.5%-12% | 单峰分布,集中在3%附近 |
| 挥发酸占比对评分影响 | 低占比易得高分 | 无显著趋势 |
| 总酸对评分影响 | 无显著趋势 | 无显著趋势 |
| pH对评分影响 | 低pH得高分,趋势微弱 | 高pH得高分,趋势微弱 |
| 按柠檬酸分类 | 属于(干、半干、半甜)类 | 99%属于(干、半干、半甜)类,只有2例甜葡萄酒 |
| 残留糖对评分影响 | 无显著趋势,高含量在中间分段 | 无显著趋势,高含量在中间分段 |
| 按残留糖分类 | 干、半干、半甜 | 干、半干、半甜、甜 |
| 酒精浓度对评分影响 | 高浓度易得高分 | 高浓度易得高分 |
| 氯化物对评分影响 | 低浓度得高分,趋势微弱 | 低浓度得高分,趋势微弱 |
| 硫酸盐对评分影响 | 高浓度易得高分 | 无显著趋势 |
| 游离二氧化硫占总量比分布情况 | 分布分散大多数在10%-60% | 单峰分布,集中在25%附近 |
| 游离二氧化硫占比对评分影响 | 无显著趋势 | 无显著趋势 |
| 二氧化硫总量对评分影响 | 无显著趋势 | 无显著趋势 |
| 密度对评分影响 | 低密度易得高分 | 低密度易得高分 |
- 红葡萄酒品质主要与固定酸含量(柠檬酸)、酒精浓度、硫酸盐浓度正相关,与挥发酸含量、pH值、氯化物浓度、密度负相关;
- 白葡萄酒品质主要与pH值、酒精浓度正相关,与氯化物、密度负相关;
- 对两种葡萄酒而言,总酸含量、残留糖含量、二氧化硫都是没有什么影响力的变量
- 从变量样本分布情况来看,两种葡萄酒存在明显区别,故在成分含量上对红、白葡萄酒进行区分较为可行:
- 11种输入变量之间普遍相关性不大,仅少数具有较高相关性,因此不具备理想的降维条件,无法将11种输入变量整合为少数几个综合变量(对红、白葡萄酒均是如此)。
参考资料
- Seaborn 箱型图学习笔记
- atplotlib:subplot绘制多个子图
- Matplotlib画条形图和柱形图并添加数据标注
更新记录:
数据集取自天池官方,天池平台也有对于该数据集的分析案例,本篇在之基础上做了一定取舍与扩展,算是重头自己做了一遍,如有分析不严谨之处欢迎交流指正。
- 2020.5.7 初稿完成