【机器学习】kNN算法
一、问题引入
k近邻法(k-nearest neighbor, k-NN)是一种基本分类方法,属于非概率模型,可以处理二类或多类问题。相比之前介绍过的Logistic回归、朴素贝叶斯、支持向量机这些复杂的分类模型相比,这个模型则显得简单很多了。它在文本分类、预测分析、模式识别、图像处理等各个领域都有广泛的应用。kNN的中心指导思想可以用一句经典的中国古话概况:近朱者赤,近墨者黑。它无需根据你的特征向量比如性格、爱好之类的去建立什么数学模型,仅凭你身边的人大多是什么类型就可以判定你是一个什么类型的人。这种简单直观的方法往往符合我们很多人日常交际思维,因此它解决一些简单的问题还是比较有效的。当然咯,仅从一个人身边的人来判断他是一个什么人有时会显得很片面,假如他是一个出淤泥而不染的人呢?下面我们正式讨论这个算法。
二、问题分析
1.k近邻算法简单、直观:给定一个训练数据集,对新的输入实例,在训练数据集中找到与该实例最邻近 的k个实例,这k个实例的多数属于某个类,就把该输入实例分为这个类。该算法计算步骤如下:
(1)算距离:给定的输入实例,计算它与训练集中所有样本点的距离;
(2)找近邻:划定与输入实例最邻近的k个样本点,作为测试近邻;
(3)投票表决:少数服从多数。把测试样本中实例最多的类别作为输入实例的分类输出。一条公式概况如下:
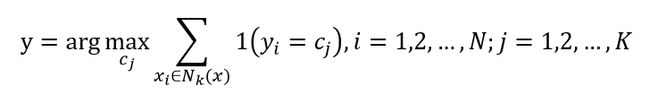
因此,k近邻法没有显示的学习过程。那么问题来了,距离的衡量是怎么样的?
2.距离度量
最一般性的距离度量是Lp距离:

这里p≥1.特别地,当p=2时,称为欧氏距离:
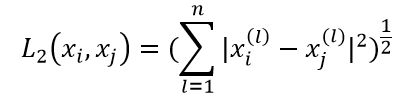
当p=1时,称为曼哈顿距离;当p=∞时,它是各个坐标距离的最大值。欧氏距离是算法中最常用的。在二维的情况下,初中生都知道是用勾股定理来算的。
3.K值的选择
这也是一个关键的问题,它对算法的结果产生重大影响。如果k比较小,就相当于算法划定的近邻范围比较小,此时只有与输入实例非常相似的实例才会对预测结果产生影响,但缺点就是估计误差会增大,就是说,万一近邻的实例是噪声,预测就会出错。简单地说,k值减小就意味着整体模型变得复杂,容易发生过拟合。反之,如果k值较大,可以减少估计误差,但缺点就是近似误差会增大,此时与输入实例距离较远的实例也会对预测产生影响,k值增大就意味着整体的模型变得简单。
三、代码实现(Matlab)
%% 随机生成数据
N1 = 100; N2 = 30; % 类别1样本点数100个,类别2样本点数30个
x = [randn(N1,2);randn(N2,2)+3];
y = [zeros(N1,1);ones(N2,1)];
N = size(x,1); % 训练集总数
%% 绘制散点图
ma = {'bo','gs'};
fc = {[0 0 1],[0 1 0]};
yv = unique(y);
figure(1); hold off
for i = 1:length(yv)
pos = find(y==yv(i));
plot(x(pos,1),x(pos,2),ma{i},'markerfacecolor',fc{i});
hold on
end
%% 根据不同的K值生成决策边界
% 扫描所有测试实例
[Xv, Yv] = meshgrid(min(x(:,1)):0.1:max(x(:,1)),min(x(:,2)):0.1:max(x(:,2)));
classes = zeros(size(Xv));
K = 5
for i = 1:length(Xv(:))
this = [Xv(i) Yv(i)];
% 计算欧氏距离, 并排序
distances = sum((x - repmat(this,N,1)).^2,2);
[d, I] = sort(distances,'ascend');
[a, b] = hist(y(I(1:K))); % 找出距离最近的k个点
pos = find(a==max(a)); % 找出出现频率最大的类别
if length(pos) > 1
order = randperm(length(pos));
pos = pos(order(1));
end
classes(i) = b(pos);
end
figure(1); hold off
for i = 1:length(yv)
pos = find(y==yv(i));
plot(x(pos,1),x(pos,2),ma{i},'markerfacecolor',fc{i});
hold on
end
contour(Xv,Yv,classes,[0.5 0.5],'r','linewidth',2)
ti = sprintf('K = %g',K);
title(ti);
代码比较简单,没啥好说的。分别选取K=1,k=5绘制决策边界如下:
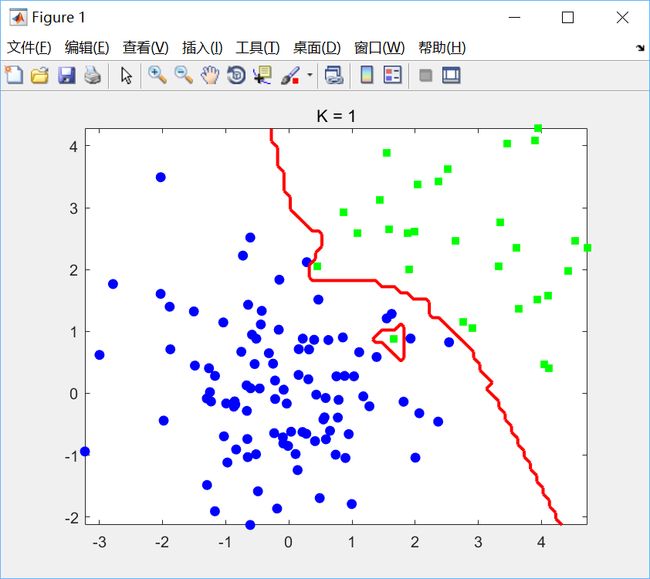
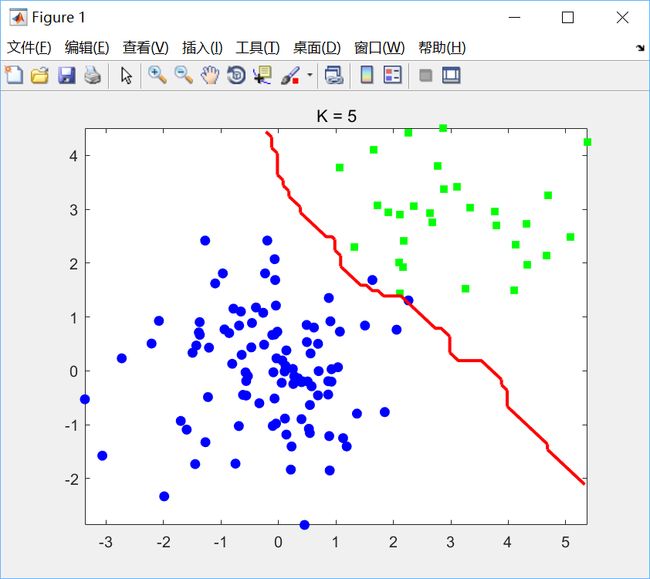
可见K值过小会产生过拟合现象。
四、总结
这个算法在机器学习领域上应该属于“学渣”级别的。相比之前介绍的算法,它们都不同程度上学习到了数据的本质特征,比如Logistic回归“学到了”sigmoid函数,朴素贝叶斯“学到了”用先验概率算后验概率,支持向量机“学到了”最大化间隔置信度最高,它们分类的时候都根据已经学习到的模型来预测结果,甚至还能给出置信度,是标准的“学霸”性算法。“学渣”算法就好比我等学渣平时对待考试的态度,临近考试(分类问题)时才临时抱佛脚,找近年的题目背一遍(相当于临时找k个近邻),最后考试背了啥就写啥(作出预测),有时这样干出来成绩还很不错(近似误差不是很大)。但是,懒惰的后果,你懂的,他了解到知识的本质了吗?并没有,考试要是难一点(训练集分布复杂)他就hold不住了。而且,由于方法过于简单粗暴,老师要是不画个重点,你不就该把所有题目都背一遍(线性扫描全部训练样本,计算开销大)?这样你还得熬几个通宵(运行效率低)。当然咯,kNN还是有它的用武之地的,应付一些凑学分的水课还是不错的,但专业课还是得认真学习(支持向量机,高斯混合模型,PCA……一个都不能少)哈哈,算法是不是很有趣呢?