缩放数据抵抗噪声

scikit-learn KNN

导入数据

import pandas as pd
%matplotlib inline
import matplotlib.pyplot as plt
plt.style.use('ggplot')
df = pd.read_csv('winequality-red.csv ' , sep = ';')
X = df.drop('quality' , 1).values # drop target variable
y1 = df['quality'].values
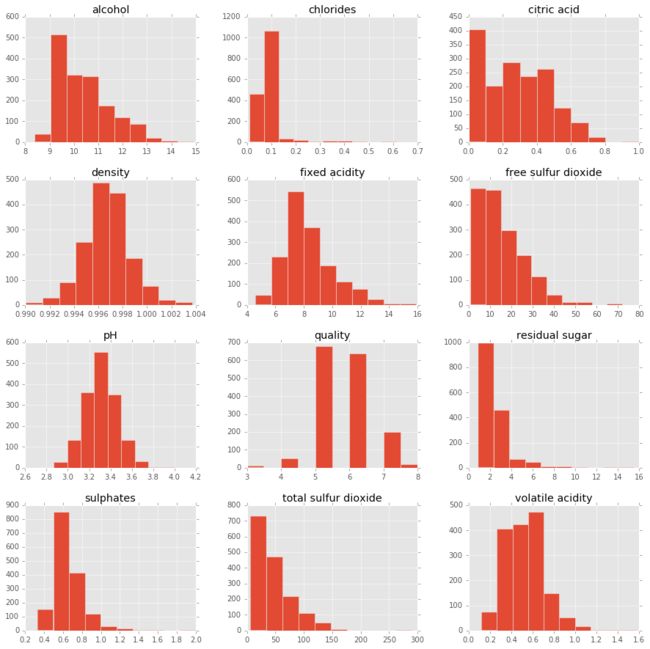
pd.DataFrame.hist(df, figsize = [15,15]);

---

回归问题转换成分类问题

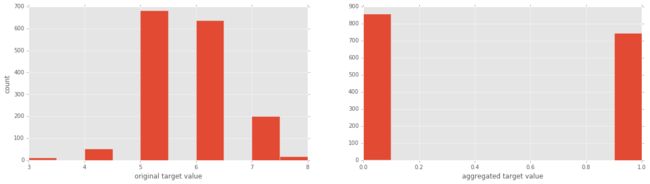
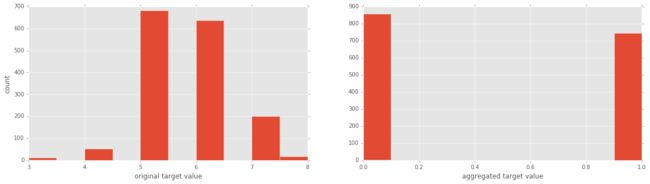
y = y1 <= 5 # is the rating <= 5?
# plot histograms of original target variable
# and aggregated target variable
plt.figure(figsize=(20,5));
plt.subplot(1, 2, 1 );
plt.hist(y1);
plt.xlabel('original target value')
plt.ylabel('count')
plt.subplot(1, 2, 2);
plt.hist(y)
plt.xlabel('aggregated target value')
plt.show()

---

性能度量指标：

• 准确率（Accuracy）:正确预测数目除以总的预测数目。
• 精度（Precision）:真阳性样例数目除以真和假阳性样例数目
• 召回率（recall）: 用真阳性样例数目除以真阳性和假阴性样例数目。
• F1-score:精度和召回率的调和平均数。

---

划分数据为训练集和测试集

from sklearn.cross_validation import train_test_split
X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.2, random_state=42)

• test_size：测试集大小比率
• random_state: 随机数生成器种子

---

训练和测试模型

from sklearn import neighbors, linear_model
knn = neighbors.KNeighborsClassifier(n_neighbors = 5)
knn_model_1 = knn.fit(X_train, y_train)
print('k-NN accuracy for test set: %f' % knn_model_1.score(X_test, y_test))

k-NN accuracy for test set: 0.612500

---

导出模型的分类报告

from sklearn.metrics import classification_report
y_true, y_pred = y_test, knn_model_1.predict(X_test)
print(classification_report(y_true, y_pred))

             precision    recall  f1-score   support

      False       0.66      0.64      0.65       179
       True       0.56      0.57      0.57       141

avg / total       0.61      0.61      0.61       320

False,True 分别是反例和正例样本

---

预处理机制：缩放和中心化

是预处理数值型数据最基本的方法。

• 标准化，所有的标准化操作就是将数据集缩放，使其最小值为0，最大值为1。为实现这一目标，我们将数据点x变换成 ：
  
  xnormalized=x−xminxmax−xmin
• 规范化，将数据向0集中，使用标准差进行缩放：
  
  xnormalized=x−μσ
  
  μ和σ分别表示数据集的平均值和标准差。这些变换仅仅改变数据的范围而没有改变其分布。之后你可能会使用其他的变换，比如log变换或者Box-Cox变换，让数据更像高斯分布（如钟形曲线）。

---

预处理：缩放实战

from sklearn.preprocessing import scale
Xs = scale(X)
from sklearn.cross_validation import train_test_split
Xs_train, Xs_test, y_train, y_test = train_test_split(Xs, y, test_size=0.2, random_state=42)
knn_model_2 = knn.fit(Xs_train, y_train)
print('k-NN score for test set: %f' % knn_model_2.score(Xs_test, y_test))
print('k-NN score for training set: %f' % knn_model_2.score(Xs_train, y_train))
y_true, y_pred = y_test, knn_model_2.predict(Xs_test)
print(classification_report(y_true, y_pred))

k-NN score for test set: 0.712500
k-NN score for training set: 0.814699
             precision    recall  f1-score   support

      False       0.72      0.79      0.75       179
       True       0.70      0.62      0.65       141

avg / total       0.71      0.71      0.71       320

scikit-learn LR

数据可视化

# Import necessary packages
import pandas as pd
%matplotlib inline
import matplotlib.pyplot as plt
plt.style.use('ggplot')
from sklearn import datasets
from sklearn import linear_model
import numpy as np
# Load data
boston = datasets.load_boston()
yb = boston.target.reshape(-1, 1)
Xb = boston['data'][:,5].reshape(-1, 1)
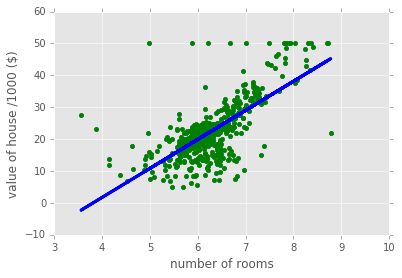
# Plot data
plt.scatter(Xb,yb)
plt.ylabel('value of house /1000 ($)')
plt.xlabel('number of rooms')
# Create linear regression object
regr = linear_model.LinearRegression()
# Train the model using the training sets
regr.fit( Xb, yb)
# Plot outputs
plt.scatter(Xb, yb,  color='g')
plt.plot(Xb, regr.predict(Xb), color='blue',
         linewidth=3)
plt.show()

---

逻辑回归python实现

逻辑函数：

F(x)=11+e−(ax+b)

这是一条sigmoidal（S形）曲线，如下图。对于任意x，如果F(x)<0.5，那么逻辑模型给出预测y=0，相反，如果F(X)>0.5，那么模型预测y=1。在有多个预测变量的情况下，我们有n个系数a1,…,an，每一个对应一个预测变量。在这种情况下，ai的大小告诉我们对应变量对预测变量的影响程度。

# Synthesize data
X1 = np.random.normal(size=150)
y1 = (X1 > 0).astype(np.float)
X1[X1 > 0] *= 4
X1 += .3 * np.random.normal(size=150)
X1= X1.reshape(-1, 1)
X1_ordered = sorted(X1)
# Run the classifier
clf = linear_model.LogisticRegression()
clf.fit(X1, y1)
# Plot the result
plt.scatter(X1.ravel(), y1, color='black', zorder=20 , alpha = 0.5)
plt.plot(X1_ordered, clf.predict_proba(X1_ordered)[:,1], color='blue' , linewidth = 3)
plt.ylabel('target variable')
plt.xlabel('predictor variable')
plt.show()

---

逻辑回归和数据缩放：红酒数据集

# Import necessary modules
from sklearn import linear_model
from sklearn.cross_validation import train_test_split
# Load data
df = pd.read_csv('winequality-red.csv ' , sep = ';')
X = df.drop('quality' , 1).values #drop target variable
y1 = df['quality'].values
y = y1 <= 5 # is the rating <= 5?
# plot histograms of original target variable
# and aggregated target variable
plt.figure(figsize=(20,5));
plt.subplot(1, 2, 1 );
plt.hist(y1);
plt.xlabel('original target value')
plt.ylabel('count')
plt.subplot(1, 2, 2);
plt.hist(y)
plt.xlabel('aggregated target value')
plt.show()

运行下逻辑回归看看效果如何！

数据缩放前

# Split the data into test and training sets
X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.2, random_state=42)
#initial logistic regression model
lr = linear_model.LogisticRegression()
# fit the model
lr = lr.fit(X_train, y_train)
print('Logistic Regression score for training set: %f' % lr.score(X_train, y_train))
from sklearn.metrics import classification_report
y_true, y_pred = y_test, lr.predict(X_test)
print(classification_report(y_true, y_pred))

Logistic Regression score for training set: 0.752932
             precision    recall  f1-score   support

      False       0.78      0.74      0.76       179
       True       0.69      0.74      0.71       141

avg / total       0.74      0.74      0.74       320

数据缩放后

from sklearn.preprocessing import scale
Xs = scale(X)
Xs_train, Xs_test, y_train, y_test = train_test_split(Xs, y, test_size=0.2, random_state=42)
lr_2 = lr.fit(Xs_train, y_train)
print('Scaled Logistic Regression score for test set: %f' % lr_2.score(Xs_test, y_test))
y_true, y_pred = y_test, lr_2.predict(Xs_test)
print(classification_report(y_true, y_pred))

Scaled Logistic Regression score for test set: 0.740625
             precision    recall  f1-score   support

      False       0.79      0.74      0.76       179
       True       0.69      0.74      0.72       141

avg / total       0.74      0.74      0.74       320

使用数据缩放后，逻辑回归的性能并没有提升。为什么会这样，特别是我们看到在k-NN上使用缩放性能大幅提升之后？其原因在于，如果有大范围的预测变量，它们不会影响目标变量，回归算法会将相应的系数ai调小，这样它们就不会对预测有太大影响。k-NN没有这种内置的策略，所以我们需要缩放数据。

缩放数据对模型影响量化分析

使用滋扰变量（不会影响目标变量但会影响模型）形式的噪声来看看它会对缩放前后的模型有何影响，合成一个数据集，在此可以控制滋扰变量的确切性质合成数据噪声越大，缩放对k-NN越重要。

---

blob产生数据

# Generate some clustered data (blobs!)
import numpy as np
from sklearn.datasets.samples_generator import make_blobs
n_samples=2000
X, y = make_blobs(n_samples, centers=4, n_features=2,
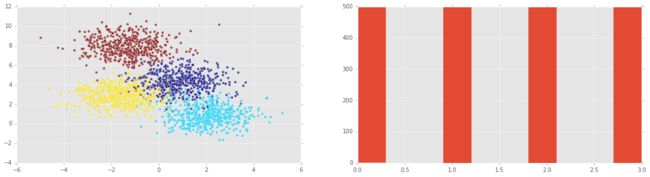
                  random_state=0)

---

绘制合成数据

%matplotlib inline
import matplotlib.pyplot as plt
plt.style.use('ggplot')
plt.figure(figsize=(20,5));
plt.subplot(1, 2, 1 );
plt.scatter(X[:,0] , X[:,1],  c = y, alpha = 0.7);
plt.subplot(1, 2, 2);
plt.hist(y)
plt.show()

注意：我们可以在第二幅图中看到所有可能的目标变量都均等。在这种情况下（或者它们大致均等），我们说类y是平衡的。

import pandas as pd
df = pd.DataFrame(X)
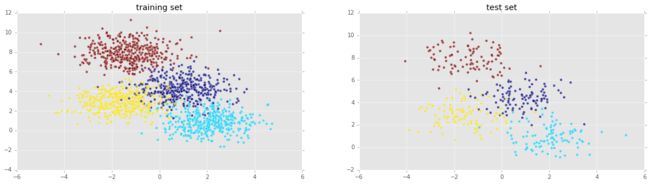
pd.DataFrame.hist(df, figsize=(20,5));

---

分割和绘制测试集和训练集

from sklearn.cross_validation import train_test_split
X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.2, random_state=42)
plt.figure(figsize=(20,5));
plt.subplot(1, 2, 1 );
plt.title('training set')
plt.scatter(X_train[:,0] , X_train[:,1],  c = y_train, alpha = 0.7);
plt.subplot(1, 2, 2);
plt.scatter(X_test[:,0] , X_test[:,1],  c = y_test, alpha = 0.7);
plt.title('test set')
plt.show()

---

数据缩放前KNN性能

from sklearn import neighbors, linear_model
knn = neighbors.KNeighborsClassifier()
knn_model = knn.fit(X_train, y_train)
print('k-NN score for test set: %f' % knn_model.score(X_test, y_test))
from sklearn.metrics import classification_report
y_true, y_pred = y_test, knn_model.predict(X_test)
print(classification_report(y_true, y_pred))

k-NN score for test set: 0.935000
             precision    recall  f1-score   support

          0       0.87      0.90      0.88       106
          1       0.98      0.93      0.95       102
          2       0.90      0.92      0.91       100
          3       1.00      1.00      1.00        92

avg / total       0.94      0.94      0.94       400

---

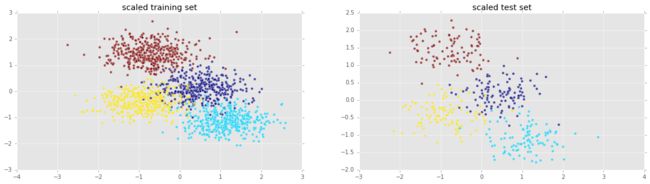
缩放数据

from sklearn.preprocessing import scale
Xs = scale(X)
Xs_train, Xs_test, y_train, y_test = train_test_split(Xs, y, test_size=0.2, random_state=42)
plt.figure(figsize=(20,5));
plt.subplot(1, 2, 1 );
plt.scatter(Xs_train[:,0] , Xs_train[:,1],  c = y_train, alpha = 0.7);
plt.title('scaled training set')
plt.subplot(1, 2, 2);
plt.scatter(Xs_test[:,0] , Xs_test[:,1],  c = y_test, alpha = 0.7);
plt.title('scaled test set')
plt.show()

数据缩放后KNN性能

knn_model_s = knn.fit(Xs_train, y_train)
print('k-NN score for test set: %f' % knn_model_s.score(Xs_test, y_test))
from sklearn.metrics import classification_report
y_true, y_pred = y_test, knn_model_s.predict(Xs_test)
print(classification_report(y_true, y_pred))

k-NN score for test set: 0.935000
             precision    recall  f1-score   support

          0       0.87      0.92      0.89       106
          1       0.98      0.92      0.95       102
          2       0.91      0.92      0.92       100
          3       1.00      0.99      0.99        92

avg / total       0.94      0.94      0.94       400

使用缩放对性能并没有任何改进！这大概是因为所有特征都处于同一范围内。当各种变量范围差别巨大时，缩放才有意义。想看看它的实际作用，我们将会加入另外一个特征。此外，该特征将与目标变量无关：这纯粹是噪声。

---

在信号中加入噪声

我们加入高斯噪声变量，均值为0，变量标准差为 σ 。我们称 σ 为噪声强度，我们会看到，噪声强度越大，k近邻性能越差。

# Add noise column to predictor variables
ns = 10**(3) # Strength of noise term
newcol = np.transpose([ns*np.random.randn(n_samples)])
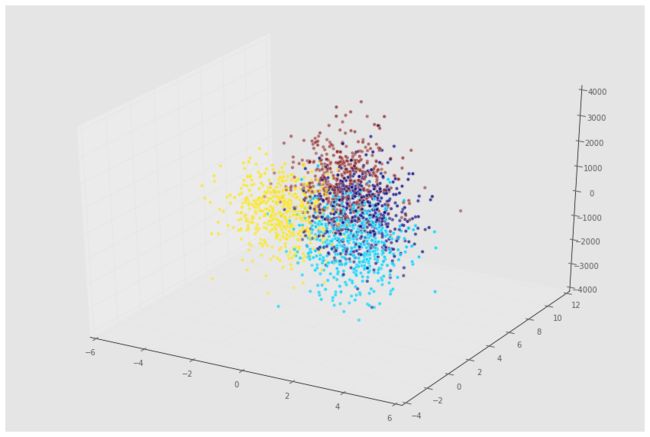
Xn = np.concatenate((X, newcol), axis = 1)

mplot3d包来绘制数据3D图：

from mpl_toolkits.mplot3d import Axes3D
fig = plt.figure(figsize=(15,10));
ax = fig.add_subplot(111, projection='3d' , alpha = 0.5);
ax.scatter(Xn[:,0], Xn[:,1], Xn[:,2], c = y);

加入噪声以后的数据缩放前性能

Xn_train, Xn_test, y_train, y_test = train_test_split(Xn, y, test_size=0.2, random_state=42)
knn = neighbors.KNeighborsClassifier()
knn_model = knn.fit(Xn_train, y_train)
print('k-NN score for test set: %f' % knn_model.score(Xn_test, y_test))
from sklearn.metrics import classification_report
y_true, y_pred = y_test, knn_model.predict(Xn_test)
print(classification_report(y_true, y_pred))

k-NN score for test set: 0.397500
             precision    recall  f1-score   support

          0       0.31      0.44      0.37       106
          1       0.45      0.38      0.41       102
          2       0.43      0.44      0.44       100
          3       0.48      0.32      0.38        92

avg / total       0.42      0.40      0.40       400

加入噪声以后的数据缩放后性能

Xns = scale(Xn)
s = int(.2*n_samples)
Xns_train = Xns[s:]
y_train = y[s:]
Xns_test = Xns[:s]
y_test = y[:s]
knn = neighbors.KNeighborsClassifier()
knn_models = knn.fit(Xns_train, y_train)
print('k-NN score for test set: %f' % knn_models.score(Xns_test, y_test))
from sklearn.metrics import classification_report
y_true, y_pred = y_test, knn_models.predict(Xns_test)
print(classification_report(y_true, y_pred))

k-NN score for test set: 0.937500
             precision    recall  f1-score   support

          0       0.85      0.93      0.89        87
          1       0.97      0.95      0.96       103
          2       0.93      0.91      0.92       110
          3       1.00      0.96      0.98       100

avg / total       0.94      0.94      0.94       400

缩放数据之后，模型的性能与加入噪声之前差的很多。

---

噪声越大，问题越大

现在我们使用噪声强度函数来看看模型性能的变化。

在KNN上测试

def accu( X, y):
    X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.2, random_state=42)
    knn = neighbors.KNeighborsClassifier()
    knn_model = knn.fit(X_train, y_train)
    return(knn_model.score(X_test, y_test))

noise = [10**i for i in np.arange(-1,6)]
A1 = np.zeros(len(noise))
A2 = np.zeros(len(noise))
count = 0
for ns in noise:
    newcol = np.transpose([ns*np.random.randn(n_samples)])
    Xn = np.concatenate((X, newcol), axis = 1)
    Xns = scale(Xn)
    A1[count] = accu( Xn, y)
    A2[count] = accu( Xns, y)
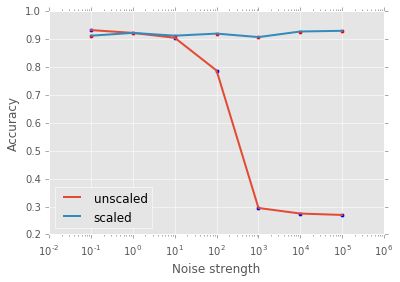
    count += 1

plt.scatter( noise, A1 )
plt.plot( noise, A1, label = 'unscaled', linewidth = 2)
plt.scatter( noise, A2 , c = 'r')
plt.plot( noise, A2 , label = 'scaled', linewidth = 2)
plt.xscale('log')
plt.xlabel('Noise strength')
plt.ylabel('Accuracy')
plt.legend(loc=3);

滋扰变量中噪声越多，在k-NN模型中缩放数据就越重要。

在LR上测试

def accu( X, y):
    X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.2, random_state=42)
    lr = linear_model.LogisticRegression()
    lr_model = lr.fit(X_train, y_train)
    return(lr_model.score(X_test, y_test))
noise = [10**i for i in np.arange(-1,6)]
A1 = np.zeros(len(noise))
A2 = np.zeros(len(noise))
count = 0
for ns in noise:
    newcol = np.transpose([ns*np.random.randn(n_samples)])
    Xn = np.concatenate((X, newcol), axis = 1)
    Xns = scale(Xn)
    A1[count] = accu( Xn, y)
    A2[count] = accu( Xns, y)
    count += 1
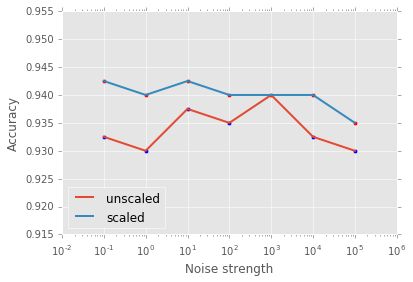
plt.scatter( noise, A1 )
plt.plot( noise, A1, label = 'unscaled', linewidth = 2)
plt.scatter( noise, A2 , c = 'r')
plt.plot( noise, A2 , label = 'scaled', linewidth = 2)
plt.xscale('log')
plt.xlabel('Noise strength')
plt.ylabel('Accuracy')
plt.legend(loc=3);

在逻辑回归中，缩放对噪声影响不大