支持向量机解决非线性问题的简单代码(初学者)
核支持向量机求解非线性问题
支持向量机可以很容易的通过核化来解决非线性化分类问题。
执行下述代码创建一个简单的数据集,调用numpy的logical_or函数形成一个异或门,其中有100个样本分类标签为1,100为-1
import matplotlib.pyplot as plt
import numpy as np
np.random.seed(1)
x_xor = np.random.randn(200,2)
y_xor = np.logical_xor(x_xor[:,0] > 0,x_xor[:,1] >0)
y_xor = np.where(y_xor,1,-1)
plt.scatter(x_xor[y_xor == 1,0],
x_xor[y_xor == 1,1],
c = 'b',marker = 'x',
label = '1')
plt.scatter(x_xor[y_xor == -1,0],
x_xor[y_xor == -1,1],
c = 'r',marker = 's', #market代表的是图形形状,其中‘x’是叉形;‘s’是方形
label = '-1')
plt.xlim([-3,3])
plt.ylim([-3,3])
plt.legend(loc = 'best')
plt.show()
执行上述代码会产生具有随机噪声的XOR数据集图片如下

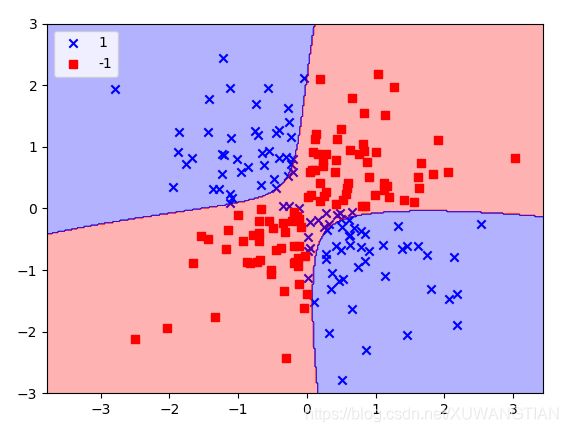
核方法的逻辑是针对线性不可分数据,建立非线性组合,通过映射函数把原始特征投影到一个高维空间,使得该特征在高维空间可分。
import matplotlib.pyplot as plt
import numpy as np
from sklearn.svm import SVC
from matplotlib.colors import ListedColormap
import pandas as pd
np.random.seed(1)
x_xor = np.random.randn(200,2)
y_xor = np.logical_xor(x_xor[:,0] > 0,x_xor[:,1] >0)
y_xor = np.where(y_xor,1,-1)
plt.scatter(x_xor[y_xor == 1,0],
x_xor[y_xor == 1,1],
c = 'b',marker = 'x',
label = '1')
plt.scatter(x_xor[y_xor == -1,0],
x_xor[y_xor == -1,1],
c = 'r',marker = 's', #market代表的是图形形状,其中‘x’是叉形;‘s’是方形
label = '-1')
plt.xlim([-3,3])
plt.ylim([-3,3])
def plot_decision_regions(x,y,classifier,resolution=0.02):
#定义marker generator and color ma
markers = ('s','x','o','^','v')
colors = ('red','blue','lightgreen','gray','cyan')
cmap = ListedColormap(colors[:len(np.unique(y))])
#plot the decision surface
x1_min,x1_max = x[:,0].min() - 1, x[:,0].max() + 1
x2_min,x2_max = x[:,1].min() - 1, x[:,1].max() + 1
xx1,xx2 = np.meshgrid(np.arange(x1_min,x1_max,resolution),np.arange(x2_min,x2_max,resolution))
z = classifier.predict(np.array([xx1.ravel(),xx2.ravel()]).T)
z = z.reshape(xx1.shape)
plt.contourf(xx1,xx2,z,alpha=0.3,cmap=cmap)
plt.xlim(xx1.min(),xx1.max())
plt.xlim(xx2.min(),xx2.max())
svm = SVC(kernel = 'rbf',random_state = 1,gamma =0.10,C = 10.0)
svm.fit(x_xor,y_xor)
plot_decision_regions(x_xor,y_xor,classifier=svm)
plt.legend(loc = 'upper left')
plt.show()