《Python智能数独说明书》源码下载...

《Python智能数独说明书》

如需获取原文档：公众号回复Python智能数独说明书。

摘 要 ：Python智能数独使用Python完成类了对数独的结果计算分析功能，该课题将使用到递归算法来实现。

关键词

数独、递归、Python。

引言

数独是我们日常生活中经常听闻的一类逻辑游戏，它源自18世纪的瑞士，是一种运用纸、笔进行演算的逻辑游戏。玩家需要根据9×9盘面上的已知数字，推理出所有剩余空格的数字，并满足每一行、每一列、每一个粗线宫（3*3）内的数字均含1-9，不重复 。

一、需求分析

1.1技术现状

随着人工智能的发展，Python技术的流行，Python也为人们的工作与生活上带来了很多的便捷。因为Python简单，学起来快，也是不少新手程序员入门的首选语言。

从自身特性Python发展Python自身强大的优势决定其不可限量的发展前景。Python作为一种通用语言，几乎可以用在任何领域和场合，角色几乎是无限的。Python具有简单、易学、免费、开源、可移植、可扩展、可嵌入、面向对象等优点，它的面向对象甚至比java和C#.net更彻底。

它是一种很灵活的语言，能帮你轻松完成编程工作。强大的类库支持，使编写文件处理、正则表达式，网络连接等程序变得相当容易。能运行在多种计算机平台和操作系统中，如各位unix，windows，MacOS,OS/2等等，并可作为一种原型开发语言，加快大型程序的开发速度。从企业应用来看Python发展Python被广泛的用在Web开发、运维自动化、测试自动化、数据挖掘等多个行业和领域。一项专业调查显示，75%的受访者将Python视为他们的主要开发语言，反之，其他25%受访者则将其视为辅助开发语言。将Python作为主要开发语言的开发者数量逐年递增。

这表明Python正在成为越来越多开发者的开发语言选择。目前，国内不少大企业都已经使用Python，如豆瓣、搜狐、金山、腾讯、盛大、网易、百度、阿里、淘宝、热酷、土豆、新浪、果壳等；国外的谷歌、NASA、YouTube、Facebook、工业光魔、红帽等都在应Python完成各种各样的任务。从市场需求与薪资看Python发展从职友集最新Python招聘岗位需求来看，Python工程师的岗位需求量巨大，并且岗位需求量还在呈现上涨的趋势。全国Python岗位需求量接近10万，北京岗位需求量居首位为20890个占比21.17%，上海Python工程师岗位需求量居第二位为12843个占比13.02%，其次是深圳、杭州、广州等一线城市合计占比16.53%，从下图可知Python 相关职位的需求量，依然集中在三大经济圈

在当今数据化信息的加持下，Python这门对数据有着天然亲和性的编程语言发展趋势如日中火。

1.2题目阐述

Python智能数独是基于Python编程语言开发的一款对数独智能计算的应用软件。该课题是使用基本的Python功能点来实现，例如Python实现递归算法、实现数据的拆解分析等分析型编程特性的软件。其功能点如下：

Python算法解数独。

递归实现。

二、具体实现

2.1应用架构

应用采用C/S两层架构，应用端完全负责完成与用户的交互任务。在大部分使用情况下只需考虑客户机的性能指标而无需其它额外条件。

2.2系统环境

此程序在Windows10 & 64位系统上基于Python语言使用IntellIJ IDEA 2019开发编写，源代码请在该环境下运行调试。

2.3运行要求

运行源程序请尽量使系统自身可使用RAM不低于1GB，可使用ROM不低于1GB。

该程序使用IntellIJ IDEA 2019开发，如需调试源代码请尽量保持环境一致，如有非同出现的程序结果不相符情况请自行调试更改。编译源代码请尽量使系统自身可使用RAM不低于2GB，可使用ROM不低于2GB。

2.4设计思路

对递归算法进行初步了解，直接使用代码表达为

#斐波那契数列通项公式

def f(n):
    if n == 1:
        return 1
    elif n == 2:
        return 1
    else:
        a =  f(n-1) + f(n-2)
        return a

斐波那契数列，用数学表达式就是：

f(1) = 1,f(2) = 1
若n>2，则f(n) = f(n-1)+f(n-2)

其实这里就已经应用了递归！若求f(5)的值，则必须求f(4)和f(3)的值，若求f(4)和f(3)的值，则需要求f(3),f(2)和f(2)和f(1)的值，f(2)和f(1)是我们已知的值，然后就可以依次求出f(3),f(4)直到f(5)的值。我们可以用数学表达式演示一下：

--> f(5) = f(4) + f(3) 
--> f(4) = f(3) + f(2) , f(3) = f(2) + f(1) 
--> f(3) = f(2) + f(1) , f(2) = 1 , f(2) = 1 , f(1) = 1
--> f(2) = 1 , f(1) = 1
--> f(3) = 2 , f(2) = 1 , f(2) = 1 , f(1) = 1
--> f(4) = 3 , f(3) = 2
--> f(5) = 5

这个斐波那契数列的例子，就用到了递归，当n > 2时，我们返回的不是一个常数，而是f(n-1)+f(n-2)，即在f(n)中“直接或间接调用自身”。

在使用trial()递归函数之前，数独各个单元格的值域如下图

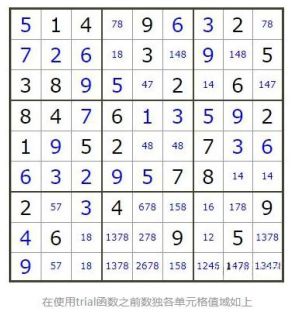
单元格值域长度为1的单元格会被自动跳过，因为他们都是已知单元格了。第1行第4列的单元格，有2个可选值，我们先假设值为7，然后缩减整个数独各个单元格的值域.我们发现新得到的值域列表有问题，soduku_checkRepeat()函数检测到有重复值，因此第1行第4列的单元格取值不是7，我们继续循环赋值8；赋值8后，使用reduce_totalValueRange()缩减各个单元格值域，使用soduku_checkRepeat()函数检测没有重复值，然后继续用sodukuRate()函数检测，发现每个单元格值域长度均为1，则正确答案找到了，返回test_value即是最终答案。

·

# 主函数，输入值域列表，如遇到多个取值的单元格，依次尝试值域里的每个值，通过递归的方法检测值是否正确
def trial(total_value_range):
    for i in range(9):
        for j in range(9):
            if len(total_value_range[i][j]) > 1:
                for k in total_value_range[i][j]:
                    test_value = copy.deepcopy(total_value_range)
                    test_value[i][j] = [k]
                    test_value = reduce_totalValueRange(generator_soduku(test_value))
                    if soduku_checkRepeat(test_value):
                        if sodukuRate(test_value) == 1:
                            return test_value
                        else:    
                            if trial(test_value):
                                return trial(test_value)
                    else:
                        continue
                return False

2.5代码实现

具体代码见附录代码。

2.6代码改进

基于具体的2.5代码实现，我对整体代码做出了优化，将“递归”充分的应用在改课题实现中，前后共改进3个版本，具体代码参见附录

三、实验结果

3.1逻辑结果分析

串一下递归函数的处理逻辑：

• 第一步：单元格值域长度为1的单元格会被自动跳过，因为他们都是已知单元格了

• 第二步：第1行第3列的单元格，有2个可选值，我们先假设值为4，然后缩减整个数独各个单元格的值域

v第三步：新得到的值域列表通过soduku_checkRepeat()函数检测没有发现重复值，我们继续用sodukuRate()函数检测，发现有单元格值域长度不为1

• 第四步：关键的地方来了，在这种情况下，我们执行的是else: if trial(test_value)语句，也就是把当前的值域列表test_value作为参数，代入trail()函数中，这里我们就用到递归了；

• 第五步：那么我们就看下，将当前的test_value代入trial()函数，会发生什么

• 第六步：递归的第二层函数运行结束了，返回的是False，即第一层trial()函数运行到此处，实际上运行的是else: if False ，if下面的语句不执行，将会执行else: continue，也就是说对于最开始的值域列表，第1行第3列的单元格值不是4，我们要继续遍历取下一个值——7，然后缩减整个数独各个单元格的值域

• 第七步：新得到的值域列表通过soduku_checkRepeat()函数检测没有发现重复值，我们继续用sodukuRate()函数检测，发现有单元格值域长度不为1；

• 第八步：继续执行else: if trial(test_value)语句

• 第九步：trial(test_value)返回了一个数组，因此if后是一个布尔值为True的值，执行if后的语句，return trial(test_value)，这里相当于把第八步流程又走了一遍，第二层trial()返回的是正确答案数组

v第十步：回到第一层trial()函数，这次将返回正确答案数组

经过该课题的实验，我们在代码层面深入了解类什么是递归以及运用递归来解密数独，对于数独的解题上有着不同的思路与设计实现，具体采用需根据实际运用来分析实现。

四、结论

我们用到的解题算法：

递归：

程序调用自身的编程技巧称为递归（ recursion）。递归做为一种算法在程序设计语言中广泛应用。 一个过程或函数在其定义或说明中有直接或间接调用自身的一种方法，它通常把一个大型复杂的问题层层转化为一个与原问题相似的规模较小的问题来求解，递归策略只需少量的程序就可描述出解题过程所需要的多次重复计算，大大地减少了程序的代码量。递归的能力在于用有限的语句来定义对象的无限集合。一般来说，递归需要有边界条件、递归前进段和递归返回段。当边界条件不满足时，递归前进；当边界条件满足时，递归返回。

五、参考文献

《Python算法教程》、《Python核心》

六、附录

版本发行：V1.0,V1.1, V1.2

完整说明书与代码请参见：《Python智能数独说明书》

如需获取原文档：公众号回复 Python智能数独说明书 。

公众号：三千IT屋