用 Python 编程解数独的思路和源码（LeetCode Problem 37）

最近做了LeetCode上关于数独的题目，下面将问题描述、解题思路和源码分享如下，希望网友们批评指正：

问题描述

编写程序通过填写空白单元格来解数独。

一个数独的解需要满足下列条件：

1. 数字1-9每行每个数字只能出现一次。
2. 数字1-9每列每个数字只能出现一次。
3. 数字1-9在9个3×3的小方格里每个数字只能出现一次。

空白的单元格用字符“.”表示。

一个数独问题示例

它的解法用红色数字标记

补充说明：

• 给出的表格元素只包括字符1-9和“.”。
• 你可以假设给出的数独题目只有一个解。
• 给出的表格一定是9×9的

解题思路

我们（为什么写博客也用我们，又不是写论文w(ﾟДﾟ)w，等等，我除了毕业论文之外也没写过论文-_-~！）先不着急想这道题的解法如何用程序编写出来，比如：是用DFS（深度优先搜索），还是剪枝，还是回溯，还要不要用到Hash表（虽然题目标签(Related Topics)里标明了是Hash表和回溯 -_-~！）。在这里我们先讨论人类是如何用手动的方法解数独的。

人工解法

我们还是以题目中的示例为例。用board[i][j]表示第i行第j列元素。为了和编程习惯统一，我们从0开始数数。首先看board[0][2]的元素，第0行已经有了[5,3,7]三个数字；第2列已经有了[8]；第0个3×3的小方格里已经有了[5,3,6,9,8]五个数字。所以board[0][2]只可能是[1,2,4]中的一个。

首先我们试着让board[0][2] = 1（最小值）。再看board[0][3]的元素，同理可以得到board[0][3]只可能是[2,6]中的一个，试着让board[0][3] = 2（最小值）。

类似的我们可以一直填到board[0][7] = 9，这时表格如下（右下角的小数字表示前面的值已经填完之后，该单元格填写数字的其他可能情况）：

这时发现board[0][8]没有数字可以填了，于是我们换种可能，擦掉board[0][7]的9并试着让board[0][6] = 9再接着做下去。就这样不断地试错，直到都填完了为止。

编程实现

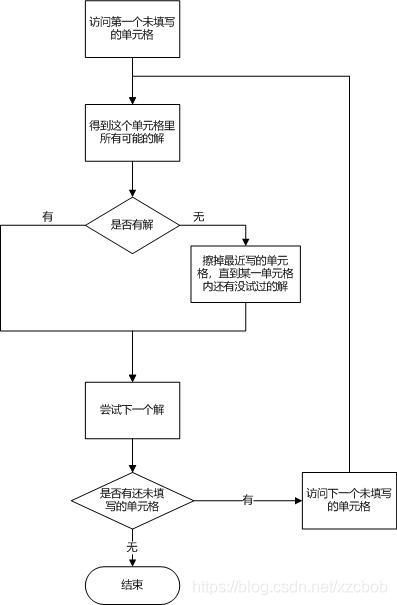
根据人类的解法我们可以得到解数独的大致思路如下：

 

由此我们可以给出源程序如下，详细解释参考注释：

#anslist = ''
'''
这是网络上看到的最难数独，用作测试样例，其格式和LeetCode上的样例不同
主体程序中有相应的转换过程
sodokuboard = [[8, 0, 0, 0, 0, 0, 0, 0, 0],
          [0, 0, 3, 6, 0, 0, 0, 0, 0],
          [0, 7, 0, 0, 9, 0, 2, 0, 0],
          [0, 5, 0, 0, 0, 7, 0, 0, 0],
          [0, 0, 0, 0, 4, 5, 7, 0, 0],
          [0, 0, 0, 1, 0, 0, 0, 3, 0],
          [0, 0, 1, 0, 0, 0, 0, 6, 8],
          [0, 0, 8, 5, 0, 0, 0, 1, 0],
          [0, 9, 0, 0, 0, 0, 4, 0, 0]]
'''
class Solution:
    def solveSudoku(self, board) -> None:
        line  = []
        row   = []
        chunk = []
        '''
        这三个变量都由9行列表组成，用来表示每一行（列、3×3小块）中缺少的数字（即空白单元格中可以填写的数字）
        比如line[0]=[1,2,3]表示第一行还缺少[1,2,3]三个数
        其他两个同理
        '''
        unsolved = []
        '''
        unsolved中记录了还未填写的单元格的坐标[x,y]
        '''
        solved = []
        '''
        solved中记录了已填写的单元格的坐标和数值[x,y,value]
        '''
        for i in range(9):
            temp = [1,1,1,1,1,1,1,1,1]
            templi = []
            for j in range(9):
                if board[i][j] != '.':
                    temp[int(board[i][j])-1] -= 1
                
                else:
                    unsolved.append([i,j])
                
            for j in range(9):
                if temp[j] == 1:
                    templi.append(str(j+1))
            line.append(templi)

        for i in range(9):
            temp = [1,1,1,1,1,1,1,1,1]
            templi = []
            for j in range(9):
                if board[j][i] != '.':
                    temp[int(board[j][i])-1] -= 1
            for j in range(9):
                if temp[j] == 1:
                    templi.append(str(j+1))
            row.append(templi)

        for i in range(9):
            temp = [1,1,1,1,1,1,1,1,1]
            templi = []
            lineindex = int(i/3)*3
            rowindex = i%3*3
            for j in range(9):
                x = lineindex + int(j/3)
                y = rowindex + j%3
                if board[x][y] != '.':
                    temp[int(board[x][y])-1] -= 1
            for j in range(9):
                if temp[j] == 1:
                    templi.append(str(j+1))
            chunk.append(templi)
        '''
        上面三个for循环分别求得了line，row，chunk列表的内容，并顺便求得了unsolved中的内容
        当然，最好写成一个for循环，以减少运算次数和简化代码，写成三个只是让可读性更好一些

        下面调用递归函数，求得solved列表，即ans
        '''

        ans = sodoku(unsolved,solved,line,row,chunk)

        '''
        调试用
        with open('out2.txt','w+') as f:
            f.write(anslist)
        #print(ans)
        '''

        '''
        这个for循环负责将solved列表中的内容填到board中
        '''
        for x in ans:
            i,j,k = x
            board[i][j] = k
        
        '''
        调试用
        for x in board:
            print(x)
        '''
        
def sodoku(unsolved,solved,line,row,chunk):
    #global anslist
    if len(unsolved) > 0:
        ansset = []
        x,y = unsolved[0]
        '''
        下面的for循环求得了[x,y]单元格中的所有解集
        求法为取该单元格所在的line，row，chunk列表的交集
        '''
        for i in line[x]:
            if i in row[y] and i in chunk[int(y/3)+int(x/3)*3]:
                ansset.append(i)
        
        for i in ansset:
            line[x].remove(i)
            row[y].remove(i)
            chunk[int(y/3)+int(x/3)*3].remove(i)
            solved.append([x,y,i])
            '''填写好答案表格改变之后更新line，row，chunk，solved列表'''
            ans = sodoku(unsolved[1:],solved,line,row,chunk)
            if ans:
                return ans
            line[x].append(i)
            row[y].append(i)
            chunk[int(y/3)+int(x/3)*3].append(i)
            solved.pop()
            '''当尝试失败时还原line，row，chunk，solved列表'''
    else:
        return solved
'''
调试用
if __name__ == '__main__':
    so = Solution()
    #so.solveSudoku([["5","3",".",".","7",".",".",".","."],["6",".",".","1","9","5",".",".","."],[".","9","8",".",".",".",".","6","."],["8",".",".",".","6",".",".",".","3"],["4",".",".","8",".","3",".",".","1"],["7",".",".",".","2",".",".",".","6"],[".","6",".",".",".",".","2","8","."],[".",".",".","4","1","9",".",".","5"],[".",".",".",".","8",".",".","7","9"]])
    for i in range(9):
        for j in range(9):
            if sodokuboard[i][j] == 0:
                sodokuboard[i][j] = '.'
            else:
                sodokuboard[i][j] = str(sodokuboard[i][j])
    so.solveSudoku(sodokuboard)
'''

以上就是文章的全部内容，希望可以帮到大家，文章内容如有不足或者错误，恳请大家批评指正。