python自然语言处理实战核心技术与算法——HMM模型代码详解
本人初学NLP,当我看着《python自然语言处理实战核心技术与算法》书上这接近200行的代码看着有点头皮发麻,于是我读了接近一天基本把每行代码的含义给读的个七七八八,考虑到可能会有人和我一样有点迷茫,所以写下这篇文章与大家分享。
目录
- 一、HMM模型与Viterbi算法
- 1. HMM模型
- 2. Viterbi算法
- 二、代码讲解
- 1. __ init __(self):
- 2. try_load_model(self, trained):
- 3. train(self, path):
- 3.1 init_parameters():
- 3.2 make_label(text):
- 3.3 其余代码
- 4. viterbi(self, text, states, start_p, trans_p, emit_p):
- 5.cut(self, text):
- 三、代码与效果展示
- 1. 代码
- 2. 效果演示
- 四、参考
一、HMM模型与Viterbi算法
1. HMM模型
HMM模型的核心是:从可观察的参数中确定该过程的隐含参数。
在本例子中,可观察的参数是句子或者说每个字,隐含参数是每个字的标签。
这里还要提到韩梅梅模型的两个假设:
-
观测独立性假设:每个字的输出仅仅与当前字有关;即:
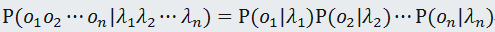
当然,从概率论的公式也可以推导出,这些事件都是相互独立的,也反推了“观测独立性”。 -
齐次马尔科夫假设:每个输出仅仅与上一个输出有关。即:

关于齐次马尔科夫假设为什么只与上一个输出有关,是因为语言模型中有一个名叫n元模型的存在,这里推荐一篇文章讲解这个模型:NLP(二):n元模型注:o:B、M、E、S这四种标签;λ:句子中的每个字(包括标点等非中文字符)。
每个字的标签作者分为了4个,即B:词首;M:词中;E:词尾;S:单独成词。我不知道会不会有人和我之前一样混淆了词语与句子的关系,但是我这里还是要说明一下,帮大家排下坑。这里的词首 != 句首,虽然肯定句首也是个词,无论是词首还是单独成词,但是不能一概而论,因为一句话里面肯定只有一个句首,但是会有无数个词语,这个在后面讲代码的时候会再讲到,之后再详谈。
HMM模型中有3个概率:
- 初始概率:自然语言序列中第一个字λ1的标记是ok的概率,即π = P(λ1 = ok)
- 发射概率:即输出概率,就是隐含状态输出可见状态的概率,P(λk|ok)
- 转移概率:由前一个隐含状态转移到另一个隐含状态的概率,P(ok|ok-1)
由于本文核心不是讨论该模型的概念,所以我这里放上一个我刚看韩梅梅模型的时候看到的一篇博客,说实话,有点让人高潮,链接如下:一文搞懂HMM(隐马尔可夫模型)
2. Viterbi算法
这是一种动态规划的算法,其核心思想是:如果最终的最优路径经过某个oi,那么从初始节点到oi-1点的路径必然也是一个最优路径,因为每一个节点oi只会影响前后两个P(oi-1|oi)和P(oi|oi+1)。
关于维特比算法,给大家推荐这篇文章,讲的十分浅显易懂,一分钟解决维特比算法概念:如何通俗地讲解 viterbi 算法?
二、代码讲解
回归正题,由于代码好几百行,为了保证大家的阅读质量与逻辑梳理,我将这个HMM类分开为方法,依据我认为实际编程时搭建的步骤来进行讲解。先看一下代码框架:

1. __ init __(self):
大家都知道,__init__方法都是用来初始化的,我在注释上写明了每个参数的说明,这里就贴代码,不多赘述了。
# 提取文件hmm_model.pkl
# 主要用于存取算法中间结果,不用每次都训练模型
self.model_file = './data/hmm_model.pkl'
# 状态值集合
self.state_list = ['B', 'M', 'E', 'S']
# 参数加载,用于判断是否需要重新加载model_file
self.load_para = False
2. try_load_model(self, trained):
这个方法主要也是进行初始化的,只不过是先判断我们的是否训练过,如果训练过就直接加载中间文件,节省系统开销,没训练过则进行相应的训练。
def try_load_model(self, trained):
"""
判别加载中间文件结果。
当直接加载中间结果时,可以不通过语料库训练,直接进行分词调用。
否则该函数用于初始化初始概率、转移概率以及发射概率等信息。(当需要重新训练时,需要初始化清空结果)
:param trained: 是否需要直接加载中间结果:
True: 加载; False: 初始化清空结果
:return:
"""
if trained:
with open(self.model_file, 'rb') as f:
self.A_dic = pickle.load(f)
self.B_dic = pickle.load(f)
self.Pi_dic = pickle.load(f)
self.load_para = True
else:
# 状态转移概率 P(ok | ok-1)
self.A_dic = {}
# 发射概率 P(λk | ok)
self.B_dic = {}
# 状态的初始概率 P(λ1 = ok)
self.Pi_dic = {}
self.load_para = False
需要注意的是文件打开这里,因为打开的文件是.pkl类型,这是python保存的一种文件类型,而.pkl是二进制文件不是文本文件,所以需要rb方式才能打开。
3. train(self, path):
这是训练的方法,训练的依据为:
通过给定的分词语料进行训练,计算转移概率、发射概率和初始概率。
语料格式为每行一句话,逗号隔开也算依据,每个词以空格分隔。
里面封装了两个函数,先从函数开始说:
3.1 init_parameters():
def init_parameters():
"""
初始化参数
Pi_di: 初始概率,为列向量,直接赋值为0
A_dic: 转移概率,因为转移情况只有16种,只是概率不同,所以可以先把标签给上并赋值0.0
B_dic: 发射概率,因为并没有训练,所以里面为空
count_dic: 统计每个标签出现的次数
转移概率表明了: 从某个隐含状态转移到另一个(包括自己)隐含状态的概率
输出概率表明了: 从某个隐含状态输出可见状态的概率
:return:
"""
for state in self.state_list:
self.A_dic[state] = {s: 0.0 for s in self.state_list}
self.Pi_dic[state] = 0.0
self.B_dic[state] = {}
count_dic[state] = 0
这里的state是指的每一个标签,即“B”,“M”,“E”,“S”。
关于这里初始化为何是这样,是因为如下:
- 对于转移概率矩阵A_dic,因为大家都知道,转移是从一个状态转移到另一个状态,而状态(标签)我们已经是确定了的,也就是只有16种情况,即{{B→B,B→M,B→E,B→S}…},所以这里可以直接确定字典里面的内容,并且先赋值概率为0.0。
- 对于初始概率矩阵Pi_dic,这是一个列向量,毕竟是初始概率,每一句只会有第一个字记录,所以整体矩阵为[“B”, “M”, “E”, “S”]T,这里也就可以直接给每一列的概率赋值给0.0.
- 对于发射概率矩阵B_dic,因为我们还没开始训练,不清楚究竟有哪些汉字,也不清楚每个汉字对应的标签,所以这里给一个空的字典。
- 关于count_dic[state]是用于统计每个标签出现的次数,后续会讲解到,这里先一笔带过。
3.2 make_label(text):
这个是为输入的文本赋值标签的操作,先上代码:
def make_label(text):
"""
根据传入文本的字数来给这个小词语的每个字赋予一个标签
:param text: 传入的词语
:return out_text: 该词语中每个字出现位置的标签列表
"""
out_text = []
if len(text) == 1:
# 如果只有一个字,则归类为S
out_text.append('S')
else:
# 否则返回B,M,E
# 因为长度大于1,所以至少2个字,如果是多个字,那么在这个词中第一个字肯定是B,最后一个肯定是E,其余的为M
out_text += ['B'] + ['M'] * (len(text) - 2) + ['E']
return out_text
这里传入的text是一个一个的小词语而不是整个句子,后面的代码中会有讲解,这里先有这么个概念。
那么对于词语,一般来说都是两个字以上的,所以如果只有一个字,那么这个肯定是“S”(单独成词);而如果多个字,那么我们就依据字出现的位置来进行标签赋值,可能有些同学想象力不够(比如我),光看这个公式有点莫名其妙,我这里以一个词语“秃然”和成语“聪明绝顶”来讲解。
我们先看“秃然”,len(“秃然”)大于1,所以进入else,而len(“秃然”) - 2 = 0,所以[“M”]这个就为0,那么整个out_text = [‘B’, ‘E’],而我们再回忆下,B为begin,E为end,那么是不是"秃"就是这个词语的begin,"然"就是这个词语的end了?
"聪明绝顶"也一样,[‘M’] * (len(“聪明绝顶”) - 2) = 2,整个out_text = [‘B’, ‘M’, ‘M’, ‘E’],那么’聪’是begin,'明’和’绝’为middle,'顶’为end。
综上所述,整个中间的含义为:去掉词首和词尾后,中间汉字共有多少个。
3.3 其余代码
def train(self, path):
"""
通过给定的分词语料进行训练,计算转移概率、发射概率和初始概率
语料格式为每行一句话,逗号隔开也算依据,每个词以空格分隔
:param path: 训练文件所在路径
:return self: 返回该类的实例
"""
# 重置概率矩阵
self.try_load_model(False)
# 统计每个标签的出现次数,求P(o)
count_dic = {}
def init_parameters():...
def make_label(text):...
init_parameters()
line_num = -1
# 观察者集合,主要是字以及标点等
words = set() # 无序不重复的元素序列
with open(path, encoding='utf8') as f:
for line in f:
line_num += 1 # 计算一共有多少行,用于后面计算初始概率
line = line.strip() # 除去首位空格
if not line:
# 如果本行为空,则跳过本轮循环
continue
word_list = [i for i in line if i != ' '] # 除去空格后的每一行句子的列表
# 更新字的集合 words = words | set(word_list),
# 即更新words,使words和set(word_list)中的字全部去重后加入到words中
words |= set(word_list)
line_list = line.split() # 以空格为分隔符,将文本切片为一个列表
line_state = []
for w in line_list:
# 循环列表中的每一个字或词,获得make_label(w)中的结果,追加到line_state中
line_state.extend(make_label(w))
assert len(word_list) == len(line_state) # 断言,如果词语长度不等于状态长度,则报异常
for k, v in enumerate(line_state): # 将列表组合为一个索引序列,包括数据下标和数据本身,比如(0, 'B')
count_dic[v] += 1 # 该标签出现次数 + 1
if k == 0:
self.Pi_dic[v] += 1 # 每个句子的第一个字的状态,用于计算初始状态概率
else:
self.A_dic[line_state[k - 1]][v] += 1 # 用于计算转移概率,即从上一个标签转移到这个标签发生了多少次
# 用于计算发射概率,在该状态下每出现一个这个字,这个字的次数 + 1,如果没有,则加入该字典中
self.B_dic[line_state[k]][word_list[k]] = self.B_dic[line_state[k]].get(word_list[k], 0) + 1.0
# 第一个字每个标签出现次数 / 句子个数 = 初始概率
self.Pi_dic = {k: v * 1.0 / line_num for k, v in self.Pi_dic.items()}
# 统计所有转移的次数,转移次数 / 这个标签出现次数 = 转移概率
self.A_dic = {k: {k1: v1 / count_dic[k] for k1, v1 in v.items()} for k, v in self.A_dic.items()}
# 数据稀疏问题: 由于训练样本不足而导致所估计的分布不可靠的问题
# 有可能出现某个数据(比如名字)就导致整个词语出现的概率为0
# 问题提出:
# 研究表明,语言中只有很少的常用词,大部分词都是低频词。
# 将语料库的规模扩大,主要是高频词词例的增加,大多数词(n元组)在语料中的出现是稀疏的,
# 因此扩大语料规模不能从根本上解决稀疏问题。
# 解决方案:
# 平滑: 1. 把在训练样本中出现过的事件的概率适当减小;
# 2. 把减小得到的概率质量分配给训练语料中没有出现过的事件;
# 3. 这个过程有时候也称为减值法(discounting)。
# 但是最简单的策略是"加1平滑",
# 加1平滑: 规定n元组比真实出现次数多一次,没有出现过的n元组的概率不再是0,而是一个较小的概率值,实现了概率质量的重新分配
# 统计在每个标签中出现每个字的次数,该次数 / 这个标签出现的次数 = 发射概率
self.B_dic = {k: {k1: (v1 + 1) / count_dic[k] for k1, v1 in v.items()} for k, v in self.B_dic.items()} # 序列化
# 保存数据到pkl文件中
with open(self.model_file, 'wb') as f:
pickle.dump(self.A_dic, f)
pickle.dump(self.B_dic, f)
pickle.dump(self.Pi_dic, f)
return self
我基本上每一行代码都给了注释,这里就只用挑几个我觉得比较重要的来讲解。
上文提到的关于count_dic[state]字典的作用这些也就是在这里使用了,用于计算概率,具体的在代码中有相应的注释,大家可以看代码配合上下文的解释进行理解。
首先是概率计算这一块,要从for循环这里开始说:
- 初始字标签统计:这个是最简单的一个了,就是只需要把第一个字出现的标签+1就行了,毕竟列向量嘛。
- 转移标签统计:首先我们来明确下k和v的含义,k是索引,v是标签,所以这里统计的方式是:从k - 1的字的状态到k字的状态每出现一次就+1.
- 发射统计:有了上面这句话,那么这个也好理解了,就是在k字的状态获得k字的出现次数。
对于下面概率的计算,说明如下:
- 初始概率计算:k:标签名称;v:该标签出现的次数。为什么v要乘以1.0,就是避免这个不是浮点数类型,相除之后出错。我这里给一个运行结果大家更方便理解:
Pi_dic.items(): dict_items([('B', 173416.0), ('M', 0.0), ('E', 0.0), ('S', 124543.0)])
- 转移概率计算:k:转移前的标签名;v:转移后的标签字典;k1:转移后的标签名;v1:转移后这个标签出现的次数。明白了这个后整个计算过程就没啥难度了,运行结果如下:
A_dic.items(): dict_items([('B', {'B': 0.0, 'M': 162066.0, 'E': 1226466.0, 'S': 0.0}), ('M', {'B': 0.0, 'M': 62332.0, 'E': 162066.0, 'S': 0.0}), ...])
- 发射概率计算:k:发射这个字的标签名;v:发射的字的集合;k1:发射的汉字;v1:发射该汉字的次数。这里最主要的是讲解“+1平滑”,为什么需要+1平滑?就是因为很有可能我们有个低频词比如“肏”(现在大多写成草、操、艹等),那么我们就算扩大训练集,出现这个字的频率估计也不会出现对吧,不仅增加了复杂度,而且也达不到我们想要的效果,为了防止这种某个低频字出现概率为0,最简单的方法就是+1,那么这就是一个趋近于0的出现频率但并非0,避免了这样的情况。运行结果如下:
B_dic.items(): dict_items([('B', {'中': 12812.0, '儿': 464.0, '踏': 62.0, '全': 7279.0, '各': 4884.0,...}...)])
4. viterbi(self, text, states, start_p, trans_p, emit_p):
接着是维特比算法,这一块主要是在最后判断最后一个字的时候这里还有些许没有弄懂,在注释中写明了我个人的理解,如果后续有新的理解或者认识会进行更改:
def viterbi(self, text, states, start_p, trans_p, emit_p):
"""
维特比算法: 动态规划方法
如果最终的最优路径经过某个oi,那么从初始节点到oi-1点的路径必然也是一个最优路径
因为每一个节点oi只会影响前后两个P(oi-1 | oi)和P(oi | oi+1)
:param text: 输入的需要切分的文本内容
:param states: 状态值集合
:param start_p: 初始概率 Pi_dic
:param trans_p: 转移概率 A_dic
:param emit_p: 发射概率 B_dic
:return prob: 最佳路径的概率
:return path[state]: 最佳路径
"""
V = [{}] # 记录输入的文本中每个字属于每个标签的概率
path = {} # 标签
for y in states:
V[0][y] = start_p[y] * emit_p[y].get(text[0], 0) # 计算这个文本的第一个字属于4个标签的概率
path[y] = [y]
for t in range(1, len(text)):
# 循环这个文本的第二个字到最后(因为第一个字是属于初始概率)
V.append({}) # 列表中新增一个字典(用于存放第二个字以及之后的字出现标签的概率)
new_path = {}
# 检查训练的发射概率矩阵中是否有该字
never_seen = text[t] not in emit_p['S'].keys() and \
text[t] not in emit_p['M'].keys() and \
text[t] not in emit_p['E'].keys() and \
text[t] not in emit_p['B'].keys()
for y in states:
# 循环4个标签
# 设置未知字单独成词,未知字的发射概率设置为1
# 这句话翻译为: 如果这个字在训练结果中没有没见过,那么发射概率为这个字的发射概率,否则为1.0
p_emit = emit_p[y].get(text[t], 0) if not never_seen else 1.0
# 如果t - 1的字的y0标签出现过,那么t这个字取: t - 1字y0标签出现的概率 * 从y0转移到y的转移概率 * 发射概率 中最大值
# 即state是t这个字从y0转移到y最有可能出现的t - 1时刻的标签,prob是t这个字从y0转移到y取到state标签的概率
# y0是t - 1的字出现过的标签
# 如果最终的最优路径经过某个oi,那么从初始节点到oi-1点的路径必然也是一个最优路径
(prob, state) = max(
[(V[t - 1][y0] * trans_p[y0].get(y, 0) * p_emit, y0)
for y0 in states if V[t - 1][y0] > 0
])
V[t][y] = prob # 从y0转移到y,第t个字取到第y个标签的最有可能的概率,每次添加的概率又成为下一轮循环的前一个节点概率
new_path[y] = path[state] + [y] # 从t - 1字到t字的路径,如:如果t字是B标签,那么t - 1字最优结果是S标签
path = new_path # 更新路径
# 个人理解: 最后一个字如果出现M的概率比S大(因为按理来说处于中间位置的标签不该最后出现),
# 那么极有可能因为是二元模型,历史信息较少判断出错,所以需要重新判断这个字标签为E和M的概率,
# 而如果最后一个字单独成词,那么要再看看有没有其他的可能性
if emit_p['M'].get(text[-1], 0) > emit_p['S'].get(text[-1], 0):
# 如果最后一个字的标签为M的发射概率大于S,那么就取最后一个字的E或者M中最大的概率以及标签
(prob, state) = max([(V[len(text) - 1][y], y) for y in ('E', 'M')])
else:
# 如果最后一个字的标签为S的发射概率大于M,那么就取最后一个字所有标签中的最大概率和标签
(prob, state) = max([(V[len(text) - 1][y], y) for y in states])
return prob, path[state]
由于维特比算法只需要考虑最优的路径,会将其余的内容给排除掉,所以你会看到在代码中有许多max()的地方,就是选择概率最大的部分,这也是最优的情况。
5.cut(self, text):
这也是最后一个方法,切词的方法,这一部分大家可以使用数据结构的线性表来理解,即头指针begin和指向下一个元素的next指针:
def cut(self, text):
"""
切词,通过加载中间文件,调用维特比算法完成。
:param text: 输入的文本
:return:
"""
if not self.load_para:
# 如果load_para为False,那么判断文件是否存在以决定是否需要重新训练
self.try_load_model(os.path.exists(self.model_file))
# 获取维特比算法返回的最佳路径概率与最佳路径列表
prob, pos_list = self.viterbi(text, self.state_list, self.Pi_dic, self.A_dic, self.B_dic)
begin, next = 0, 0 # begin是一个词的开始,next是下一个词开始的索引
for i, char in enumerate(text):
# 将输入的文本组合为一个索引序列,i为索引,char为每个字
pos = pos_list[i] # 路径中的第i个节点
if pos == 'B':
# 如果这一节点为"B",那么begin为该索引,意思就是这一节点是这个词的开始
begin = i
elif pos == 'E':
# 如果这一节点为"E", 那么生成器生成从begin到i的内容,并且next为下一个字的开始,
# 意思就是,这个词结束了,并且next指针指向下个词开始的位置
yield text[begin: i + 1]
next = i + 1
elif pos == 'S':
# 如果这一节点为"S",那么生成器生成这个字,并且next为下一个字的开始,
# 意思就是,这个字单独成词,所以下个词开始
yield char
next = i + 1
if next < len(text):
# 如果next指针的位置比整个文本长度小,那么生成器生成后面的内容,意思就是后面的内容整体为一个词
yield text[next:]
至于yield生成器,大家可以自行查询,这里不多赘述。
主要是关于为什么判断里面不判断’M’,因为大家在训练的过程中已经看到了’M’的判定方式了,'M’大概率是属于’B’和’E’之间的(为什么说大概率,是因为维特比算法中没看懂的那部分),所以既然已经有了’E’里面的算法,把词开头和结尾都算在内了,就没有必要用更多的计算步骤来处理’M’的问题,这样可以节省一部分资源,防止开销过大。我这里用几张线性表的图,大家就可以更方便的理解上面的过程了:
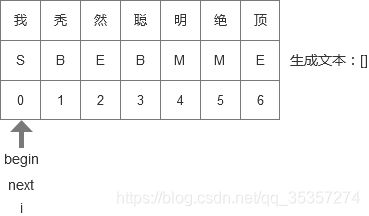
- 最开始begin和next都在线性表的第一个位置,当遇到第一个字发现是’S’,所以执行next = i + 1这一步,于是变为下图这样:
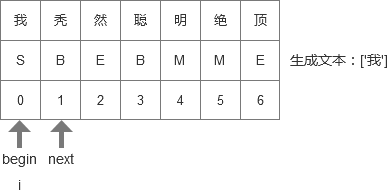
- 这时候发现’秃’是B,于是执行’B’这一步,begin = i,如下图:
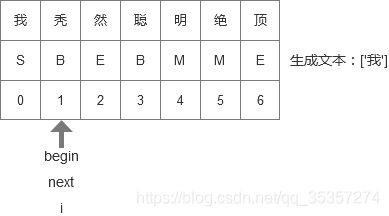
- 下一轮循环开始,i + 1,遇到’然’,这个是E,所以将’秃然’输出,然后移动next指针。如下图所示:
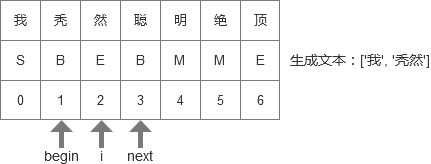
- 后面的过程就不多赘述了,就是i和begin移动到索引3的位置,然后随着i的增加,发现’明’和’绝’都是’M’,于是跳过,来到顶,也就是最后一步,输出最后一个词语,切词结束。如下图所示:

三、代码与效果展示
1. 代码
由于代码加上注释接近300行,放在这里有占篇幅的嫌疑,估计大家看着也头皮发麻,所以我放在了github上,有需要的可以自提:https://github.com/Balding-Lee/NLP_learning(数据集在data文件夹中,文件名为hidden_markov_model)
2. 效果演示

嗯,好像这句话的效果和我们预计的不太像哈,那么问题来了,为什么会是这样的?我们不妨来推测一下:
- 第一步我们肯定要看为什么’我秃然’这么刺激的东西会合并为一个词语:

那么这就说得通了,'我’这个字作为begin出现的频率最高,所以难怪会出现在词首,而’然’作为词尾出现的频率也是最高的。可能会有人问“为什么没有’秃’这个字,这个字这么没有牌面的么?”其实并不是我没有测试,而是训练集里面压根没这个字,我人傻了你知道么。
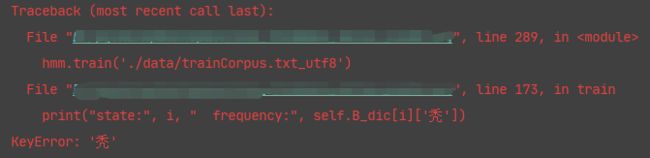
- 那么顺着上面的思路,也可以清晰地判定,在训练集中就没有“聪明绝顶”这个成语,或者说出现频率太低,直接被忽视了。
综上所述,如果想要结果准确,不仅需要我们的算法功能强大,更需要我们的数据集是很适合的。
四、参考
[1] 涂铭,刘祥,刘树春.python自然语言处理实战核心技术与算法[M].机械工业出版社:北京,2018:38.
[2] 路生.如何通俗地讲解 viterbi 算法?[EB/OL].https://www.zhihu.com/question/20136144,2020-04-09.
[3] hellozhxy.一文搞懂HMM(隐马尔可夫模型)[EB/OL].https://blog.csdn.net/hellozhxy/article/details/85254279,2018-12-25.
[4] 月臻.NLP(二):n元模型[EB/OL].https://blog.csdn.net/h__ang/article/details/88372626,2019-03-10.