机器学习学习笔记（16）----使用Matplotlib绘制决策树

在上一篇文章《机器学习学习笔记（15）----ID3（Iterative Dichotomizer 3）算法》中，我们使用ID3算法生成了一棵决策树，但是看起来并不直观，本文我们把上篇文章中的计算结果绘制成一棵决策树。

下面使用python的Matplotlib绘制决策树：

import matplotlib.pyplot as plt
from id3tree import ID3DecisionTree

class TreePlotter:

    def __init__(self, tree, feature_names, label_names):
        self.decision_node = dict(boxstyle="sawtooth", fc="0.8")
        self.leaf_node = dict(boxstyle="round4", fc="0.8")
        self.arrow_args = dict(arrowstyle="<-")
        #保存决策树
        self.tree = tree
        #保存特征名字字典
        self.feature_names=feature_names
        #保存类标记名字字典
        self.label_names=label_names
        self.totalW = None
        self.totalD = None
        self.xOff = None
        self.yOff = None
    
    def _get_num_leafs(self, node):
        '''获取叶节点的个数'''
        if not node.children:
            return 1
        num_leafs = 0
        for key in node.children.keys():
            if node.children[key].children:
                num_leafs += self._get_num_leafs(node.children[key])
            else:
                num_leafs += 1
        return num_leafs
    
    def _get_tree_depth(self, node):
        '''获取树的深度'''
        if not node.children:
            return 1
        max_depth = 0
        for key in node.children.keys():
            if node.children[key].children:
                this_depth = 1 + self._get_tree_depth(node.children[key])
            else:
                this_depth = 1
            if this_depth > max_depth:
                max_depth = this_depth
        return max_depth
        
    def _plot_mid_text(self, cntrpt, parentpt, txtstring, ax1) :
        '''在父子节点之间填充文本信息'''
        x_mid = (parentpt[0] - cntrpt[0])/2.0 + cntrpt[0]
        y_mid = (parentpt[1] - cntrpt[1])/2.0 + cntrpt[1]
        ax1.text(x_mid, y_mid, txtstring)
    
    def _plot_node(self, nodetxt, centerpt, parentpt, nodetype, ax1):
        ax1.annotate(nodetxt, xy= parentpt,\
            xycoords= 'axes fraction',\
            xytext=centerpt, textcoords='axes fraction',\
            va="center", ha="center", bbox=nodetype, arrowprops= self.arrow_args)
        
    def _plot_tree(self, tree, parentpt, nodetxt, ax1):
        #子树的叶节点个数，总宽度
        num_leafs = self._get_num_leafs(tree)
        #子树的根节点名称
        tree_name = self.feature_names[tree.feature_index]['name']
        #计算子树根节点的位置
        cntrpt = (self.xOff + (1.0 + float(num_leafs))/2.0/self.totalW, self.yOff)
        #画子树根节点与父节点中间的文字
        self._plot_mid_text(cntrpt, parentpt, nodetxt, ax1)
        #画子树的根节点，与父节点间的连线，箭头。
        self._plot_node(tree_name, cntrpt, parentpt, self.decision_node, ax1)
        #计算下级节点的y轴位置
        self.yOff = self.yOff - 1.0/self.totalD
        for key in tree.children.keys():
            child = tree.children[key]
            if child.children:
                #如果是子树，递归调用_plot_tree
                self._plot_tree(child, cntrpt, self.feature_names[tree.feature_index]['value_names'][key], ax1)
            else:
                #如果是叶子节点，计算叶子节点的x轴位置
                self.xOff = self.xOff + 1.0/self.totalW
                #如果是叶子节点，画叶子节点，以及叶子节点与父节点之间的连线，箭头。
                self._plot_node(self.label_names[child.value], (self.xOff, self.yOff), cntrpt, self.leaf_node, ax1)
                #如果是叶子节点，画叶子节点与父节点之间的中间文字。
                self._plot_mid_text((self.xOff, self.yOff), cntrpt, self.feature_names[tree.feature_index]['value_names'][key], ax1)
        #还原self.yOff
        self.yOff = self.yOff + 1.0/self.totalD

    def create_plot(self):
        fig = plt.figure(1, facecolor='white')
        fig.clf()
        #去掉边框
        axprops=dict(xticks=[], yticks=[])
        ax1 = plt.subplot(111, frameon=False, **axprops)
        #树的叶节点个数，总宽度
        self.totalW = float(self._get_num_leafs(self.tree))
        #树的深度，总高度
        self.totalD = float(self._get_tree_depth(self.tree))
        self.xOff = -0.5/self.totalW
        self.yOff = 1.0
        #树根节点位置固定放在(0.5,1.0)位置，就是中央的最上方
        self._plot_tree(self.tree, (0.5,1.0), '', ax1)
        plt.show()

代码不做解释了，核心思想就是根据树的高度和宽带，来计算各个子节点的位置，并添加相关的文字注释，细节可以参考代码中的注释。

使用上篇文章隐形眼镜数据集（http://archive.ics.uci.edu/ml/machine-learning-databases/lenses/），执行如下测试代码：

>>> import numpy as np
>>> dataset = np.genfromtxt('lenses.data',dtype=np.int)
>>> X = dataset[:, 1:-1]
>>> y = dataset[:,-1]
>>> id3 = ID3DecisionTree()
>>> id3.train(X,y)
>>> features_dict = {
	0 : {'name' : 'age',
	     'value_names': { 1: 'young',
		                  2: 'pre-presbyopic',
						  3: 'presbyopic'}
	    },
    1 : {'name' : 'prescription',
	     'value_names': { 1: 'myope',
		                  2: 'hypermetrope'}
	    },
	2 : {'name' : 'astigmatic',
	     'value_names': { 1: 'no',
		                  2: 'yes'}
	    },
	3 : {'name' : 'tear rate',
	     'value_names': { 1: 'reduced',
		                  2: 'normal'}
	    }
}

>>> label_dict = {
	1: 'hard',
	2: 'soft',
	3: 'no lenses'
}

>>> from treeplotter import TreePlotter
>>> plotter = TreePlotter(id3.tree_, features_dict, label_dict)
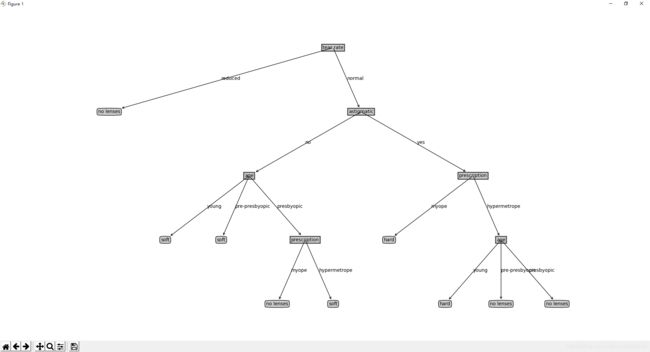
>>> plotter.create_plot()

可以得到如下的决策树：

参考资料：

《Python机器学习算法：原理，实现与案例》 刘硕 著

《机器学习实战》【美】 Peter Harringto著