同态加密在机器学习中的应用

部分文字引用自该文：崔建京, 龙军, 闵尔学, et al. 同态加密在加密机器学习中的应用研究综述[J]. 计算机科学, 2018(4):46-52.

同态加密

　　Rivest等人[1]于1978年最早提出了同态加密的概念：同态加密是一种加密形式，允许用户直接对密文进行特定的代数运算，得到的数据仍是加密的结果，且与对明文进行同样的操作再将结果加密一样。同态加密若只支持加法运算，就是加法同态加密；若只支持乘法运算，就是乘法同态加密；若同时支持加法和乘法运算，就为全同态加密。

　　加密函数背后的思想是在明文中添加一个称为噪声的小值进行加密。因此，每个密文都有少量的噪声。当我们将两个密文相加时，结果也是一个密文，但是噪声会增加。如果噪声小于一个阈值，解密函数将正常工作。阈值的存在使得在加密数据上可以执行的计算数受限。如果一方想要降低噪声，它应该对密文进行解密和加密，对于解密，它需要密钥。多年来，学界一直在试图找出一种可以在没有密钥的情况下降低噪音的方法。

　　然而，直到2009年，Gentry[2]才从数学上提出了基于理想格的全同态加密方案，对这个问题进行了回答。Am FHE方案是一种支持任意深度电路的HE方案。在论文中，Gentry介绍了一种处理任意深度计算的技术，称为bootstrapping。在bootstrapping技术中，无需访问密钥即可减少噪声量。然而，它有巨大的计算成本，是一个非常缓慢的过程。这一限制使得FHE不能实际应用。

　　HE最近的进展产生了一个更快的HE方案：层次同态加密（Leveled Homomorphic Encryption，LHE）。LHE方案不支持bootstrapping步骤，因此它们只允许深度小于特定阈值的电路。如果我们在开始计算之前知道运算的数量，我们可以使用LHE而不是FHE。采用单指令多数据（SIMD）技术进一步提高了LHE方案的性能。Halevi等人在[14]中，使用此技术创建了一批密文。因此，在计算中，一个单密文被一个密文数组所取代。

　　尽管使用HE方案有很多优点，但它们也有一些局限性。第一个是信息空间。几乎所有的HE方案都使用整数[3，4]。因此，在加密数据项之前，我们需要将它们转换为整数。第二个限制是密文大小。通过加密，信息的大小大大增加。另一个重要的限制与噪声有关。每次操作后，密文中的噪声量都会增加。乘法比加法增加的噪声更多。我们应该始终保持噪声量小于预先定义的阈值。最后一个也是最重要的限制是缺乏对除法运算的支持。总之，在加密数据上只允许有限数量的加法和乘法[5]，因此神经网络中使用的激活函数等复杂函数与HE方案不兼容。

 

Privacy-preserving Machine Learning

问题定义

　　我们需要建立一个隐私保护的深度学习系统，在这个系统中，许多学习参与者对组合后的数据集执行基于神经网络的深度学习，而实际上没有向中央服务器透露参与者的本地数据。
　　我们要实现的系统需要满足以下条件：

1. 没有向服务器泄漏任何信息；
2. 与普通的深度学习系统相比，在合并的数据集上，精度保持不变。

　　值得说明的是，直接上传梯度或者是上传部分梯度，事实上会泄露本地数据信息给诚实但好奇的服务器。

 

一、Privacy-Preserving Deep Learning via Additively Homomorphic Encryption [28]

　　作为一项直接相关的工作，Shokri和Shmatikov（ACM CCS 2015）[29]提出了一个隐私保护的深度学习系统，允许多个参与者的本地数据集，而参与者可以通过联合数据集学到神经网络模型。为了达到这个结果，在[29]中的系统需要如下：每个学习参与者，使用本地数据，首先计算神经网络的梯度；然后，这些梯度的一部分（例如1%~10%）必须发送到参数云服务器。服务器是诚实但好奇的：在提取个人数据时，它被假定是好奇的；然而，在操作中，它被假定是诚实的。

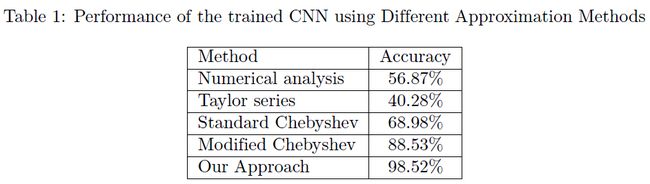
　　为了保护隐私，Shokri和Shmatikov的系统允许了一个准确性/隐私的权衡（见表1）：不共享本地梯度会导致完美的隐私，但不会带来理想的准确性；另一方面，共享所有的本地梯度会违反隐私，但会带来很好的准确性。为了妥协，在[29]中共享本地梯度的一部分是保持尽可能少的精度下降的主要解决方案。

 

 　　针对云服务器保护梯度会增加学习参与者与云服务器之间的通信成本。他们在表2中表明，增长因子并不大：对于具体数据集MNIST和SVHN，小于3。例如，在MNIST的情况下，如果每个学习参与者需要在每次上传或下载时将0.56MB的明文梯度通信到服务器；那么在他们的基于LWE的加密系统中，每次上传或下载时相应的通信成本将变为：

它需要大约8毫秒才能通过超过1 Gbps信道传输。

　　在计算方面，他们估计使用神经网络的系统在对MNIST数据集进行训练和测试时，大约在2.25小时内完成，以获得约97%的准确度。

系统

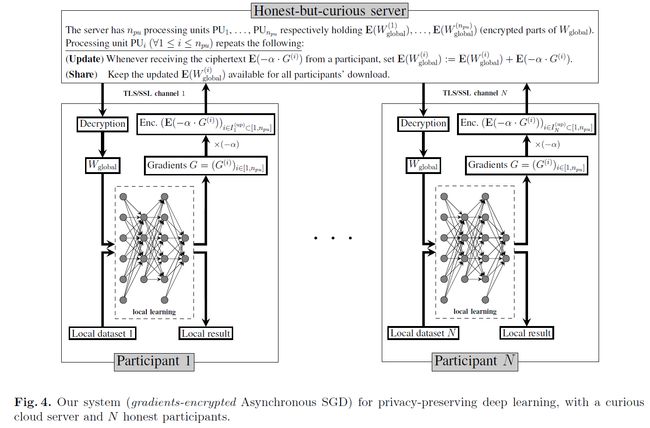
　　他们的系统如图4所示，由一个公共云服务器和N个学习参与者组成。

学习参与者：参加者共同设置公钥pk和密钥sk，以实现加法同态加密方案。密钥sk对云服务器保密，但所有学习参与者都知道。每个参与者将建立一个彼此不同的TLS/SSL安全通道，以通信和保护同态密文的完整性。同态加密方案有两种：一种是LWE-based编码（一种公钥编码方案[30]的加法同态变种[31]）；另一种是Paillier编码[32]。

　　全局模型权重W_global和梯度向量G被分为n_pu个部分，不同部分的序号参见符号上标。

　　如图4所示，每个参与者1 ≤ k ≤ N将执行以下步骤（本地模型采用的是随机梯度下降）：

云服务器：云服务器是递归更新加密权重参数的地方。特别是，服务器上的每个处理单元PU_i在接收到任何加密E(α·G⁽ⁱ⁾)后，计算

 

测试

 

　　经过2分钟的20000次迭代后，他们的TensorFlow代码在测试集中的精确度达到了97%左右。

 

同态加密机器学习

　　因此，加密机器学习不能简单地套用现有的同态加密方案，目前有两种常见的策略：１）借助安全多方计算构造适合基于同态加密的加密机器学习算法的协议，通过执行协议来完成算法（以下简称多方计算）[6]；２）寻求原有机器学习算法的近似算法，使其在不依赖交互方案的条件下，仍可以满足同态加密方案的数据及运算要求（以下简称算法近似）。

　　安全多方计算（Secure Multi-party Computation, SMC）起源于姚期智的百万富翁比较问题，主要研究如何解决一组互不信任的参与方之间保护隐私的协同计算问题。SMC要确保输入的独立性和计算的正确性，同时不泄露各输入值给参与计算的其他成员。Goldreich[7]已经证明，对于任意多项式函数，都有一个安全多方计算解决方案。因此，SMC可以作为实现基于同态加密的加密机器学习的一种手段。

　　在[6]提出的协议中，它隐藏了所有中间的神经网络计算，并且没有借助于SMC来实现激活函数的求值。简言之，NN的所有者（比如Bob）执行加密域中的所有线性计算，并委托用户（比如Alice）计算非线性函数（阈值、sigmoid等）。然而，在这样做之前，Bob会混淆激活函数的输入，这样Alice就不会了解她正在计算的内容。

　　从安全性上考虑，同态加密安全计算的协议有一个明显的弱点，即延展性攻击。延展性攻击是指，若存在恶意的竞争者获取到了处理数据方的公钥，则他可以用相同的方式对数据进行随机噪声扰动，从而使得计算无意义或使得数据发送方无法分辨接收到的是正确的结果还是攻击者的干扰。除了使用安全通道传输外，是否可以从同态加密方案的构造上预防这种威胁呢？算法近似可以一定程度上避免这个问题。

　　两种策略的优缺点如下：多方计算使用的交互式信息处理可以保持复杂运算，但涉及繁琐的协议设计，影响处理效率，且要求参与的计算方必须遵守协议才能保证正确性和安全性；而算法近似无须制定协议方案，更为贴近原有的机器学习理念，但为了避免复杂运算，对原有算法做了改变，结果的正确性不免受到影响。
　　目前，研究人员面临的问题主要有：

1. 如何在保证数据安全的前提下选择合适的同态加密方案来实现不同的数据分析；
2. 如何解决全同态加密方案中存在的噪声、运算复杂、运算效率低等问题；
3. 如何在确保算法安全性的前提下，使加密机器学习算法的性能准确度在可接受范围内。

　　当今是信息时代，因此对数据的处理格外重要。结合了机器学习算法对信息的强大分析能力和同态加密对信息的保护隐私能力的加密机器学习，具有很好的理论价值和应用前景。进一步的研究方向包括：

1. 在理论上对全同态加密方案进行深入研究，降低计算复杂度，解决密文膨胀问题；
2. 开发出支持复杂运算且具有实际应用价值的全同态加密方案；
3. 深入分析成功的机器学习算法的原理，并提出可以应用同态加密的近似算法；
4. 在已有成果的基础上，扩大已有方案的适用范围并进行性能上的优化；
5. 探讨多方计算执行流程上的简化，提高执行效率。

　　此外，随着深度学习的不断进步，隐私保护的神经网络推断（Privacy-preserving Neural Networks Inference）也受到了广泛的研究[8-17]。

 

Privacy-preserving Neural Networks Inference

问题定义

　　客户端有一个特征向量x，服务器有一个已经训练好的神经网络模型w。服务器基于模型w对x输出一个预测P（x，w）。为此，客户机向服务器发送加密输入，然后服务器执行加密推断，最后客户机获取加密预测。服务器不能了解到有关输入数据和预测的任何信息，也不能透露有关训练后的神经网络模型w的信息。

　　在实际应用中，该问题的实际解决方案应既准确（预测性能应接近明文）又高效（获得预测结果的运行时间应较短）。

 

一、CryptoNets [15]

 　　Dowlin等人于2016年提出的CryptoNets神经网络模型，是第一个提出使用FHE实现隐私保护深度学习的人。他们提供了一个框架来设计可以在加密数据上运行的神经网络，并提出使用ReLU激活函数的多项式近似。此外，他们使用的是Bos等人[18]于2013年提出的同态加密方案，YASHE‘。该方案是一种分级同态加密方案，允许对加密信息进行加、乘运算，但要求事先知道应用于数据的算术电路的复杂性。换句话说，这个密码系统允许在加密数据上计算固定最大次数的多项式函数。高阶多项式计算需要在方案中使用大参数，这会导致较大的加密消息和较慢的计算时间。因此，实际应用该系统的首要任务是将所需的计算表示为低次多项式。

　　值得注意的是，这项工作主要关注的是推断过程，建立在云端已经有训练好的模型的基础上；这套加密方案不支持浮点数。相反，他们使用固定精度的实数，通过适当的比例将其转换为整数；所有用于计算的数字不能超过2⁸⁰。同时，他们所使用的YASHE‘方案，由于Albrecht等人[20]提出的攻击而不再安全。此外，它们需要大于80位的大明文模数来适应其神经网络的输出结果，这使得其很难扩展到更深的网络，因为这些网络中的中间层在这种设置下将很快达到几百位。

 

卷积层（Convolution Layer）

　　将其前一层的矢量值乘以权重矢量，并对结果求和。权重在推断过程中是固定的。这个函数本质上是权重矢量和输送层矢量值的点积。卷积可以直接实现，因为它只使用加法和乘法。此外，这里的乘法输入是预先计算的权重和输送层的值。由于权重没有加密，因此可以使用更有效的简单乘法运算。一些网络还为卷积的结果添加了一个偏置项。为了添加这个偏置项，可以使用一个简单的加法，因为这个偏置项的值对云来说是已知的。

 

最大池化（Max Pooling）

　　计算输送层某些组分的最大值。由于取最大值函数是非线性的，所以最大池化不能直接计算。取最大值函数可以通过以下方式近似：

 

为了保持较小的数量级，d应该保持相当小的值，最小的有意义的值d=1返回的是平均池化函数的标量倍数。我们将使用这个缩放后的平均池化函数而不是最大池化函数，因为加密数据的累加求和十分便捷，而且不用进行除法运算。

 

平均池化（Mean Pooling）

　　计算输送层某些组分的平均值。

 

Sigmoid

　　取输送层中一个节点的值，并计算函数z  一> 1 / (1 + e^-z)。由于sigmoid函数是非线性的，所以需要用低次多项式对其进行近似。这里选择的是最低次的非线性多项式函数sqr(z) := z²。

 

线性整流（Rectified Linear)

　　取输送层中一个节点的值，并计算函数z 一> max(0, z)。由于线性整流函数是非线性的，所以需要用低次多项式对其进行近似。这里选择的是最低次的非线性多项式函数sqr(z) := z²。

 

网络结构

　　为了节省时间，可以合并连续的线性变换层，例如卷积层或平均池化层。该文搭建的神经网络有两种：训练用神经网络和简化神经网络，后者仅用于预测。训练用神经网络有9层，简化版有5层。其中，3-6层进行的都是线性操作，因此可以视为矩阵乘法，并组合成一层，而因为神经网络的预测由其输出向量的最大值的指标给出，最后一层的sigmoid函数是单调递增的，因此在训练完成、权值固定后可以将其丢弃。这样，简化后的神经网络就只剩下5层。

 

 

测试结果

　　MNIST（train：50000；test：10000）训练网络的准确率为98.95%

　　设备：on a PC with a single Intel Xeon E5-1620 CPU running at 3.5GHz, with 16GB of RAM, running the Windows 10 operating system.

 

 

结论

　　在加密数据上训练神经网络仍然是可能的。如果所有的激活函数都是多项式，并且损失函数也是多项式，那么只使用加法和乘法就可以计算反向传播。然而，这样做有几个挑战。计算复杂性是一个主要挑战。即使在明文上训练，神经网络训练也很慢。今天，机器学习领域的大部分工作都是通过使用诸如GPU之类的复杂硬件来加速这一训练过程。但是，向进程中添加同态加密将使进程至少慢一个数量级。由于计算出的多项式的次数与所做的反向传播步骤的数量成比例，因此使用层次同态加密似乎不可行，使得这种减速可能会更糟。加密存在的另一个挑战是缺乏数据科学家检查数据和训练好的的模型、纠正错误标记的项、添加特征和调整网络的能力。

　　这项工作的主要贡献是提出了一种在简单使用同态加密的情况下保持神经网络准确性的方法。通过将密码学、机器学习和工程技术相结合，他们能够创建一个既能实现准确性又能实现安全性的设置，同时保持较高的吞吐量水平。然而，这项工作仍有很大的改进空间。例如，通过使用GPUs和FPGAs来加速计算，可以显著提高吞吐量，降低延迟。进一步发展的另一个方向是寻找更有效的编码方案，允许更小的参数，从而进行更快的同态计算。

 

二、CryptoDL [11]

　　在该文中，他们重点关注CNN，一种最流行的深度学习算法。他们假设训练阶段是在明文数据上完成的，并且已经建立和训练了一个模型。

　　该文的主要贡献如下：

• 他们为证明在一定的误差范围内找到函数的最低度多项式逼近是可能的提供了理论基础。
• 根据理论基础，他们研究了CNNs中常用的几种激活函数（即ReLU、Sigmoid和Tanh）的近似方法，以找到最佳逼近。
• 他们在CNN中利用这些多项式，分析了改进算法的性能。
• 他们在加密数据上使用多项式近似作为激活函数来实现CNN，并报告了在两个深度学习广泛使用的数据集（MNIST，CIFAR-10）上的结果。
• 实验结果表明，该算法能达到99.52%的精度，与原模型的99.56%的精度非常接近。此外，它每小时可以做出接近164000个预测。这些结果表明，CryptoDL提供了高效、准确和可扩展的隐私保护预测。

 

多项式近似：理论基础

　　在连续函数中，多项式可能是最容易计算且表现良好的。因此，数学家倾向于用多项式来近似其他函数也就不足为奇了。本节的材料主要是数值分析中的常规知识和希尔伯特空间。

多项式近似：ReLU

　　他们研究以下方法来近似ReLU函数：

1. 数值分析
2. 泰勒级数
3. 标准切比雪夫多项式
4. 修正切比雪夫多项式
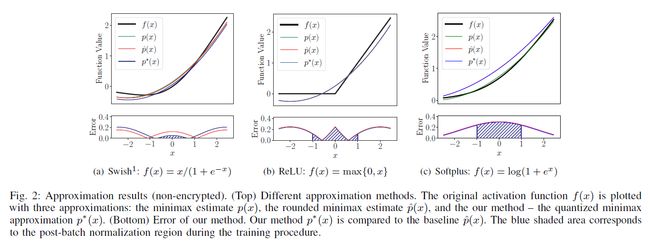
5. 他们提出的基于ReLU函数导数的方法

 

方法5：他们模拟了一个阶跃函数——ReLU函数的导数结构，而不是对ReLU函数进行逼近。Sigmoid函数是一个有界的、连续的、无穷可微的函数，在大区间内也有一个类似ReLU函数导数的结构。他们用多项式逼近了Sigmoid函数，然后计算多项式的积分，并将其作为激活函数。他们尽量使多项式的次数尽可能低，因此他们只处理次数为2和3的多项式。如表1所示，该方法实现了ReLU函数的最佳逼近。

PS：然而，我们按照作者的思路去复现，却没有成功。这是由于积分后的函数不超过3次，那么只能用二次函数去逼近Sigmoid函数，这十分不现实。若是分段后的三次函数，曲线又不能如此光滑，而且作者也没有讲他是怎么多项式逼近Sigmoid函数的，所以暂时对该结果存疑。

 

多项式近似：Sigmoid and Tanh

　　除了ReLU函数外，他们还大致分析了另外两种常用的激活函数：Sigmoid和Tanh。与ReLU相比，近似这两个函数更直接，因为它们是无限可导的。该文利用两个不同的正交多项式系统，在对称区间[-l，l]上对Sigmoid函数和Tanh函数进行多项式逼近。作为第一选择，他们考虑拉长区间上的切比雪夫多项式，来自于度量；他们的第二个选择来自于度量。

　　他们注意到，切比雪夫多项式的测度主要集中在区间的端点上，这使得插值主要发生在起始点和结束点，两端有两个奇点。而第二个度量在整条实线中均匀分布，并将零权重放在中心。这种行为在得到的近似值中引起的振荡较小，因此与Sigmoid函数的导数更为相似。

 

PS：由于激活函数的多项式近似没看懂怎么实现的，所以暂时解析到这里。（吐血三升，卒）

 

三、Faster CryptoNets [16]

激活函数近似 

　　利用他们的剪枝和量子化方案，他们的下一个贡献在于找到任何激活函数的最佳多项式近似值，给定系数必须是2的幂的约束（这与文章前面提出的方法有关，暂且不提）。神经网络的激活功能对收敛性至关重要。为了达到加密网络推断的目的，他们必须找到一种近似方法，使近似误差与实际可用性相平衡。

 

PS：暂时解析到这里。

 

四、HCNN [17]

　　他们遵循CrypoNets[15]中提出的框架，并应用他们的GPU加速FHE技术来实现高效的同态卷积神经网络（HCNNs）。

　　可求值的函数类仅限于深度为L的算术电路，生成一个可参数化的层次FHE方案，以支持深度为leqL的电路。对于性能而言，L应该最小化，这意味着他们必须仔细设计HCNN。此外，具有同态加法（HAdd）和乘法（HMult）门的算法电路的计算模型与非多项式函数（如sigmoid、ReLU和max）不兼容，这意味着他们应该尽可能地对激活函数使用多项式近似。

　　除此之外，他们必须以与FHE明文数据兼容的形式对小数进行编码，而明文数据通常是整数。它们可以具有高精度，这意味着它们将需要大比特的整数用常用的标量编码进行表示。在这种编码中，小数通过与比例因子Δ相乘转换为整数，然后正常使用HAdd和HMult操作。这种编码的主要缺点是他们不能在计算过程中重新缩放编码的数据；因此，连续的同态操作将导致数据大小快速增加。管理这种尺度展开是将HCNNs扩展到更大的数据集和更深的神经网络的必要步骤。

 

Their Contributions

1. 他们提出了第一个GPU加速同态卷积神经网络（HCNN），它对来自MNIST和CIFAR-10数据集的加密数据运行预学习模型。
2. 他们提供了一套丰富的优化技术，可以方便地设计HCNN，并减少总体计算开销。这包括低精度训练，优化选择FHE方案和参数，以及GPU加速实现。
3. 他们将MNIST数据集的HCNN减少到5层，用于训练和推断，小于训练期间使用9层的CryptoNets[15]。对于CIFAR-10，他们提供了一个11层的FHE-friendly网络，可以同时用于训练和推断。
4. 他们的实现在运行时间和准确性方面显示出高性能。在MNIST数据集上，他们的HCNN可以在8.10秒内计算整个数据集，比E2DM[19]快3.53倍。在CIFAR-10数据集上，他们的HCNN需要3044秒，比CryptoDL[11]快3.83倍。

 

 全同态加密

　　由于booststrapping算法的计算成本较高，他们采用了一种层次FHE方案，这种方案可以在不进行booststrapping的情况下，对预定乘法深度内的函数进行求值。他们选择了Brakerski-Fan-Vercauteren（BFV）方案[21，22]，该方案的安全性基于Lyubashevsky等人提出的Ring Learning With Errors（RLWE）问题[23]。这个问题被认为是很难的，即使是在量子计算机的支持下降低到最坏情况下的理想格问题（包括[23]等）。 

　　BFV方案有五种算法（KeyGen、Encrypt、Decrypt、HAdd、HMult）。KeyGen在给定所选参数的情况下，生成FHE方案中使用的密钥。Encrypy和Decrypt分别是加密和解密算法。FHE和标准公钥加密方案的区别在于对密文的操作，我们称之为HAdd和HMult。

 

神经网络

　　为了适应加密数据上的神经网络操作，他们使用以下层：

• 卷积层：在每个节点上，他们取前一层输出的一个子集，也称为滤波器，并对其执行加权和以获得其输出。
• 平均池层：在每个节点上，他们取前一层输出的一个子集，然后计算它们的平均值，得到它的输出。
• 平方层：每个节点链接到前一层的单个节点z；其输出是z的平方。
• 全连接层：与卷积层类似，每个节点输出一个加权和，但是在整个前一层上，而不是它的一个子集。

 

明文空间

　　为了简单和允许对大型数据集进行推断，他们将多个图像的相同像素打包到一个密文中，如图1所示。请注意，BFV方案可以被实例化，以便密文可能包含多个存储多个明文信息的槽。应该指出的是，这种打包方案是由CryptoNets[16]首先提出的。

 

　　他们采用标量编码，用整数逼近这些小数。这是通过将它们与比例因子Δ相乘，并将结果四舍五入到最接近的整数来完成的。然后，使用相同比例因子编码的数字可以使用整数加法或乘法组合在一起。为了简单起见，他们规范化了输入，以及在[0,1]与初始化的Δ之间的HCNNs权重，初始化的Δ对应于近似的精度位数以及近似的上限。

 

神经网络层

　　他们应用了Dowlin等人[15]发现的平方函数，对用五层网络的MNIST数据集足够得到精确结果。平均池化层是最适合FHE的。他们发现对提出的MNIST模型，池化层不是必须的；而对于CIFAR-10模型，池化层可以带来更高的精度。卷积层由于是求加权和，所以可以直接用HMultiPlain和HAdd进行运算。

 

实现

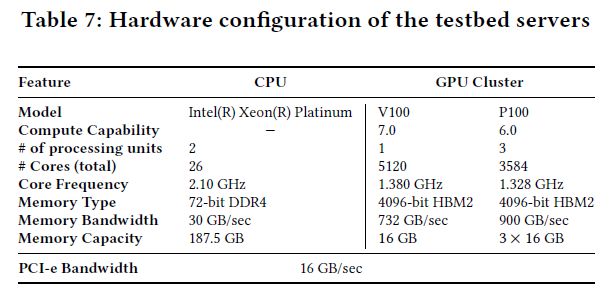
　　实现由两部分组成：1）未加密数据训练和2）加密数据分类。使用5层（用于MNIST）和11层（用于CIFAR-10）网络进行训练，详情见表1和表2。对于神经网络设计，同态加密的主要约束之一是层级权重变量数值精度的限制。低精度权重的训练网络可以有效地防止密文中的精度爆炸，提高网络深度，从而加快加密域的推断速度。他们提出从头开始训练低精度网络，与浮点精度训练的网络相比，不会造成太大的精度损失。对于每个卷积层，他们使用如下所示的简单均匀标量量化器将浮点权重变量w量化为k位数字w_q：

这个方程是一个不可微分函数，他们使用Straight Through Estimator（STE）[24]来实现反向传播。他们在MNIST训练集上对5层网络进行了2位、4位、8位和32位权重的训练，并在MNIST测试集上分别进行了精度为96%、99%、99%和99%的评估。鉴于此，他们选择4位网络进行以下实验。值得注意的是，在MNIST测试集上，CryptoNets[15]需要5到10位的权重精度才能达到99%的精度，而他们的方法进一步将其降低到4位，并且仍然在浮点和标量编码上保持相同的精度。对于CIFAR-10，由于问题更具挑战性，而且网络更深，他们的表2中所示的网络使用8位，分别使用浮点和标量编码实现77.80%和77.55%的分类精度。

 

 

　　第二部分更为复杂，因为它需要在加密数据上运行网络（使用预先学习的模型）。首先，他们固定FHE参数以适应网络乘法深度和精度。他们优化了HCNN各个方面的比例因子。对于MNIST网络，输入标准化为[0，1]，比例因子为4，然后四舍五入为最接近的整数。利用从头开始训练的低精度网络，他们将卷积层的权重转换为4位整数，使用15的比例因子；卷积中不使用任何偏差。同样，CIFAR-10网络的输入被标准化为[0，1]，但他们对卷积层使用了更大的比例因子。此外，由于它提供了更好的精度，所以使用了填充。两个网络的比例因子如表1和表2所示。

　　接下来，他们使用NTL[25]（a multi-precision number theory C++ library）来实现网络（标量编码）。NTL用于促进缩放输入的处理，并适应网络评估期间中间值的精度扩展。他们发现所需的最大精度小于MNIST的（2⁴³）和CIFAR-10的（2²⁰⁴）。请注意，对于MNIST，它足够低，可以在64位平台上容纳单个字而不会溢出。另一方面，他们使用明文CRT分解来处理CIFAR-10所需的大明文模数。通过估计网络所需的最大精度，他们可以估计HCNN所需的FHE参数。

　　下一步是使用FHE库实现网络。他们使用两个FHE库实现MNIST HCNN：SEAL[26]和如[27]所述的GPU-accelerated BFV（A*FV）。另一方面，他们只使用A*FV实现CIFAR-10 HCNN，因为它的计算量更大，而且需要很长的时间。在SEAL中实现MNIST HCNN的目的是为了便于在相同的系统参数下进行更统一的比较，并显示GPU实现的优越性。此外，需要强调的是目前在SEAL中实现的剩余数系统（Residue Number Systems，RNS）变体具有局限性。

 

实验与对比

 

 　　表10展示了以前使用FHE的工作报告结果，用来评估不同数据集上HCNN的表现。他们的解决方案在总计和平摊时间方面优于其他所有解决方案。例如，他们的MNIST HCNN比CryptoNets、E2DM和Faster CryptoNets分别快70.29倍、3.53倍和4.83倍。同样，他们的CIFAR-10 HCNN比CryptoDL快3.83倍，比Faster CryptoNets快7.35倍。

 

结论

　　在这项工作中，他们提出了一个完全基于FHE的CNN，能够用FHE对加密图像进行同态分类。这项工作的主要动机是表明通过GPU，FHE的隐私保护深度学习能够大大加快，并提供了一种有效的M/DLaaS方法。他们的实施包括一套技术，如低精度训练，统一的训练和测试网络，优化的FHE参数和一个非常有效的GPU实现，以实现高性能。他们成功地在一个CRT通道中评估了他们的MNIST HCNN，而以前的工作至少需要两个通道。他们的解决方案实现了高安全级别（>80位）和合理的精度（MNIST：99%；CIFAR-10：77.55%）。在性能方面，他们的最佳结果表明，对于MNIST和CIFAR-10，他们可以分别在6.46秒和3044秒内对整个测试数据集进行分类，每个图像的平摊时间分别为0.78毫秒和371毫秒。

　　在当前的实现中，他们的HCNN采用了简单的编码方法，将多个图像的相同像素打包成一个密文，如第3.1节所述。这种打包方案非常适合需要在单个HCNN评估中并行处理的大批量图像推断的应用。其他应用程序可能有不同的要求，例如对1个或少量图像进行分类。对于这种特殊情况，可以使用其他打包方法，将同一图像的更多像素打包到密文中。在未来的工作中，他们将研究其他适合更广泛应用的包装方法。此外，他们还将针对更大数据集和更深网络的更具挑战性的问题。

　　此外，他们注意到，使用多项式近似激活函数训练深度CNN并不能保持较高的预测精度。进一步的研究需要找到最佳的方法来近似FHE中的激活函数。

 

参考文献

[1] Rivest R L, Adleman L M, Dertouzos M L. On Data Banks and Privacy Homomorphisms[J]. Foundations of Secure Computation, 1978:169-179.

[2] Gentry C . A fully homomorphic encryption scheme[M]. Stanford University, 2009.

[3] Brakerski Z , Vaikuntanathan V . Fully Homomorphic Encryption from Ring-LWE and Security for Key Dependent Messages[C]// Advances in Cryptology - CRYPTO 2011 - 31st Annual Cryptology Conference, Santa Barbara, CA, USA, August 14-18, 2011. Proceedings. Springer, Berlin, Heidelberg, 2011.

[4] Jean-Sébastien Coron, Mandal A , Naccache D , et al. Fully Homomorphic Encryption over the Integers with Shorter Public Keys[J]. 2011. 

[5] Brakerski Z , Gentry C , Vaikuntanathan V . (Leveled) Fully Homomorphic Encryption without Bootstrapping[J]. ACM Transactions on Computation Theory, 2014, 6(3):1-36.

[6] Orlandi C , Piva A , Barni M . Oblivious Neural Network Computing via Homomorphic Encryption[J]. EURASIP Journal on Information Security, 2008, 2007(1):1-11.

[7] Goldreich O, Warning A. Secure Multi-Party Computation[J]. Information Security & Communications Privacy, 2014.

[8] Florian Bourse, Michele Minelli, Matthias Minihold, and Pascal Paillier. 2017. Fast Homomorphic Evaluation of Deep Discretized Neural Networks. IACR Cryptology ePrint Archive 2017 (2017), 1114.

[9] Hervé Chabanne, Amaury de Wargny, Jonathan Milgram, Constance Morel, and Emmanuel Prouff. 2017. Privacy-Preserving Classification on Deep Neural Network. IACR Cryptology ePrint Archive 2017 (2017), 35.

[10] Nathan Dowlin, Ran Gilad-Bachrach, Kim Laine, Kristin Lauter, Michael Naehrig, and John Wernsing. 2016. CryptoNets: Applying Neural Networks to Encrypted Data with High Throughput and Accuracy. Technical Report. https://www.microsoft.com/en-us/research/publication/cryptonets-applying-neural-networks-to-encrypted-data-with-high-throughput-and-accuracy/

[11] Ehsan Hesamifard, Hassan Takabi, and Mehdi Ghasemi. 2017. CryptoDL: Deep Neural Networks over Encrypted Data. CoRR abs/1711.05189 (2017). arXiv:1711.05189 http://arxiv.org/abs/1711.05189

[12] Jian Liu, Mika Juuti, Yao Lu, and N. Asokan. 2017. Oblivious Neural Network Predictions via MiniONN Transformations. In Proceedings of the 2017 ACM SIGSAC Conference on Computer and Communications Security (CCS ’17). ACM, New York, NY, USA, 619–631. https://doi.org/10.1145/3133956.3134056

[13] M. Sadegh Riazi, Christian Weinert, Oleksandr Tkachenko, Ebrahim M. Songhori, Thomas Schneider, and Farinaz Koushanfar. 2018. Chameleon: A Hybrid Secure Computation Framework for Machine Learning Applications. CoRR abs/1801.03239 (2018).

[14] Bita Darvish Rouhani, M. Sadegh Riazi, and Farinaz Koushanfar. 2017. DeepSecure: Scalable Provably-Secure Deep Learning. CoRR abs/1705.08963 (2017). arXiv:1705.08963 http://arxiv.org/abs/1705.08963

[15] Dowlin N, Gilad-Bachrach R, Laine K, et al. CryptoNets: Applying Neural Networks to Encrypted Data with High Throughput and Accuracy[C] // International Conference on Machine Learning(ICML). 2016:201-210.

[16] Chou E , Beal J , Levy D , et al. Faster CryptoNets: Leveraging Sparsity for Real-World Encrypted Inference[J]. 2018.

[17] Ahmad Al Badawi, Jin Chao, Jie Lin, et al. The AlexNet Moment for Homomorphic Encryption: HCNN, the First Homomorphic CNN on Encrypted Data with GPUs[J]. 2018.

[18] Bos J W , Lauter K , Loftus J , et al. Improved Security for a Ring-Based Fully Homomorphic Encryption Scheme[J]. 2013.

[19] Xiaoqian Jiang, Miran Kim, Kristin Lauter, and Yongsoo Song. 2018. Secure Outsourced Matrix Computation and Application to Neural Networks. In Proceedings of the 2018 ACM SIGSAC Conference on Computer and Communications Security (CCS ’18).

[20] Martin R. Albrecht, Shi Bai, and Léo Ducas. 2016. A Subfield Lattice Attack on Overstretched NTRU Assumptions - Cryptanalysis of Some FHE and Graded Encoding Schemes. 153–178.

[21] Zvika Brakerski. 2012. Fully Homomorphic Encryption without Modulus Switching from Classical GapSVP. 868–886.

[22] Junfeng Fan and Frederik Vercauteren. 2012. Somewhat Practical Fully Homomorphic Encryption. Cryptology ePrint Archive, Report 2012/144. (2012).

[23] Vadim Lyubashevsky, Chris Peikert, and Oded Regev. 2010. On Ideal Lattices and Learning with Errors over Rings. 1–23.

[24] Yoshua Bengio, Nicholas Léonard, and Aaron C. Courville. 2013. Estimating or Propagating Gradients Through Stochastic Neurons for Conditional Computation. CoRR (2013).

[25] Victor Shoup et al. 2005. NTL, a library for doing number theory, version 5.4. (2005).

[26] 2017. Simple Encrypted Arithmetic Library (release 2.3.1). http://sealcrypto.org. (2017). Microsoft Research, Redmond, WA.

[27] Ahmad Al Badawi, Bharadwaj Veeravalli, Chan Fook Mun, and Khin Mi Mi Aung. 2018. High-Performance FV Somewhat Homomorphic Encryption on GPUs: An Implementation using CUDA. 2018, 2 (2018), 70–95.

[28] Phong L T , Aono Y , Hayashi T , et al. Privacy-Preserving Deep Learning via Additively Homomorphic Encryption[J]. IEEE Transactions on Information Forensics and Security, 2018, 13(5):1333-1345.

[29] R. Shokri and V. Shmatikov. Privacy-preserving deep learning. In I. Ray, N. Li, and C. Kruegel, editors, Proceedings of the 22nd ACM SIGSAC Conference on Computer and Communications Security, 2015, pages 1310-1321. ACM, 2015.

[30] R. Lindner and C. Peikert. Better key sizes (and attacks) for LWE-based encryption. In A. Kiayias, editor, Topics in Cryptology - CT-RSA 2011, volume 6558 of Lecture Notes in Computer Science, pages 319{339. Springer, 2011.

[31] Y. Aono, T. Hayashi, L. T. Phong, and L. Wang. Efficient key-rotatable and security-updatable homomorphic encryption. In Proceedings of the Fifth ACM International Workshop on Security in Cloud Computing, SCC@AsiaCCS 2017, pages 35{42, 2017.

[32] P. Paillier. Public-key cryptosystems based on composite degree residuosity classes. In J. Stern, editor, Advances in Cryptology - EUROCRYPT '99, Proceeding, volume 1592 of Lecture Notes in Computer Science, pages 223-238. Springer, 1999.

转载于:https://www.cnblogs.com/lucifer1997/p/11236894.html