测试与控制技术学习笔记-第1章 信号及其描述

去年期末了才开始整理控制工程的学习比较，比较幸苦，现在就按照上课的进度来整理了。参考的教材是《机械工程测试技术基础》第三版，熊诗波，黄长艺主编。参考的网课可以从这里访问。
会以一个相对应试的角度整理知识点。不会过多地注重数学上的证明。如果发现有谬误的话，欢迎评论或者私信和我交流。

第1章 信号及其描述

1. 信号的分类与描述

1.1 信号的分类

1.1.1 确定性信号与随机信号

这张图比较好地概括了各种信号之间的关系：

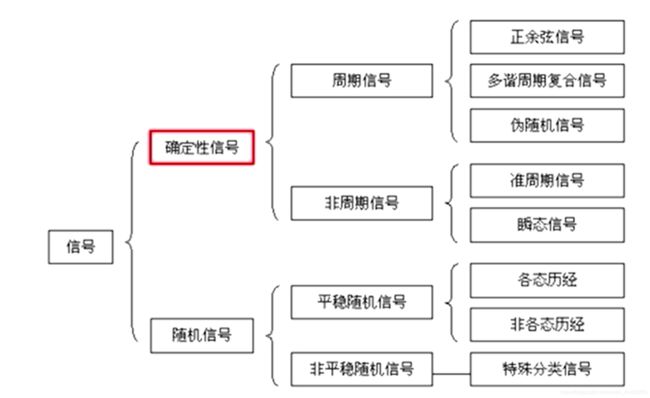
顾名思义的就不说了。一些没听说过的举例说明。
准周期信号：$x(t)=\sin t+\sin \sqrt{2}t$这个虽然画出来看起来很周期。但是由于$1$和$\sqrt{2}$没有一个有理的公约数，所以也找不到公共周期。他就并不是一个符合定义的周期信号。
平稳随机信号：一个例子是白噪声。它的统计特征量是时不变的。再下面的现在先不展开讲了。

1.1.2 连续信号和离散信号

或者也可以这么分类。

1.1.3 能量信号和功率信号

对于一个信号$x(t)$，如果它满足：
$${\int }_{-\infty }^{\infty }{x}^2(t)\mathrm{d}t<\infty$$
也就是在实数范围内积分的值是有限的，那我们我们就认为这个信号的能量是有限的，并称之为能量有限信号，简称能量信号。比如我们之前在控制工程中学过的单位脉冲信号$\delta (t)$。
如果一个信号，虽然它的${\int }_{-\infty }^{\infty }{x}^2(t)\mathrm{d}t\to \infty$但是它满足：
$$\frac{1}{t_2-t_1}{\int }_{-\infty }^{\infty }{x}^2(t)\mathrm{d}t<\infty$$
则我们称这个信号为功率有限信号，或功率信号。

1.2 信号的时域描述和频域描述

这里简单地说一下，一会儿傅里叶级数，傅里叶变换再展开。
时域描述就是我们直接观察或记录到地信号，一般以时间为独立变量，反映了信号幅值随时间地变换关系。
对于频域描述，我们需要利用一些数学工具对之进行转换。以频率为独立变量，以此来反映信号的频率结构和各频率成分与幅值、相位之间的关系。

2. 周期信号与离散频谱

2.1 傅里叶级数的三角函数展开形式

我们来回顾一下高等数学的知识：
我们可以把一个函数展开成如下形式：

$$x(t)=a_0+\sum _{n=1}^{\infty }\left(a_n\cos n{\omega }_{0}t+b_n\sin n{\omega }_{0}t\right)$$

其中：

$$\begin{array}{rl}{a}_0& =\frac{1}{T_0}{\int }_{-\frac{T_0}{2}}^{\frac{T_0}{2}}x(t)\mathrm{d}t\\ a_n& =\frac{2}{T_0}{\int }_{-\frac{T_0}{2}}^{\frac{T_0}{2}}x(t)\cos n{\omega }_{0}t\mathrm{d}t\\ b_n& =\frac{2}{T_0}{\int }_{-\frac{T_0}{2}}^{\frac{T_0}{2}}x(t)\sin n{\omega }_{0}t\mathrm{d}t\end{array}\text{\hspace{1em}(2-1)}$$

虽然老师多次要求我们把这个背出来。但我没想明白这玩意儿咋考。拉氏变换表背完不可以嘛？

2.2 傅里叶级数的复指数展开式

根据众所周知，学一次忘一次，每年开学都要重新回忆的欧拉公式：
$${\mathrm{e}}^{\pm \mathrm{j}\omega t}=\cos \omega t\pm \mathrm{j}\sin \omega t$$
我们可以把之前的式2-1进行变换。首先：
$$\begin{gathered} \cos n{\omega }_{0}t=\frac{1}{2}\left({\mathrm{e}}^{-\mathrm{j}n{\omega }_{0}t}+e^{\mathrm{j}n{\omega }_{0}t}\right) \\ \sin n{\omega }_{0}t=\mathrm{j}\frac{1}{2}\left({\mathrm{e}}^{-\mathrm{j}n{\omega }_{0}t}-e^{\mathrm{j}n{\omega }_{0}t}\right) \end{gathered}$$
进一步，代入式2-1的第一行中：
$$x(t)=a_0+\sum _{n=1}^{\infty }\left[\frac{1}{2}\left(a_n+\mathrm{j}{b}_n\right){\mathrm{e}}^{-\mathrm{j}n{\omega }_{0}t}+\frac{1}{2}\left(a_n-\mathrm{j}{b}_n\right){\mathrm{e}}^{\mathrm{j}n{\omega }_{0}t}\right]\text{\hspace{1em}(2-2)}$$
如果我们令
$$c_n=\frac{1}{2}(a_n-\mathrm{j}{b}_n)$$
考虑到$a_n$和$b_n$的奇偶性，有：
$$c_{-n}=\frac{1}{2}(a_n+\mathrm{j}{b}_n)$$
由此这个式2-2就可以变成：
$$\begin{array}{rl}x(t)& =c_0+\sum _{n=1}^{\infty }\left[c_{-n}{\mathrm{e}}^{-\mathrm{j}n{\omega }_{0}t}+c_n{\mathrm{e}}^{\mathrm{j}n{\omega }_{0}t}\right]\\ & =\sum _{n=-\infty }^{\infty }{c}_n{\mathrm{e}}^{\mathrm{j}n{\omega }_{0}t}\end{array}\text{\hspace{1em}(2-3)}$$
而这里的$c_n$有：
$$\begin{array}{rl}{c}_n& =\frac{1}{2}(a_n-\mathrm{j}{b}_n)\\ & =\frac{1}{2}\frac{2}{T_0}{\int }_{-\frac{T_0}{2}}^{\frac{T_0}{2}}(\cos n{\omega }_{0}t-\mathrm{j}\sin n{\omega }_{0}t)\mathrm{d}t\\ & =\frac{1}{T_0}{\int }_{-\frac{T_0}{2}}^{\frac{T_0}{2}}x(t){\mathrm{e}}^{-\mathrm{j}n{\omega }_{0}t}\mathrm{d}t\end{array}\text{\hspace{1em}(2-4)}$$

---

那其实有式2-3我们不难发现，一般周期函数的傅里叶级数的复指数函数形式展开后，其实频谱总是偶对称的，其虚频谱总是奇对称的。（实频谱是cos项，虚频谱是sin项，很好理解）
此外，周期函数的频谱具有三个特点：

1. 周期信号的频谱是离散的。
2. 每条谱线只出现在基波频率的整数倍上，基波频率是诸分量频率的公约数。
3. 各频率分量的谱线高度表示该谐波的幅值或相位角。在工程中的周期信号，谐波幅值总的趋势是随着谐波次数的增高而减小的。因此我们在分析的时候，频率计算的取值适可而止。

我觉得第一条和第二条可以结合之前提到的准周期信号来理解。想象一下，如果一个函数的谱线是连续的，那最小公约数那就没法取了。
这三条概括起来就是：离散型，谐波性，收敛性。

2.3 周期信号的强度表述

峰值：$x_p=|x(t){|}_{max}$
均值：${\mu }_x=\frac{1}{T_0}{\int }_0^{T_0}x(t)\mathrm{d}t$
绝对均值：${\mu }_{|x|}=\frac{1}{T_0}{\int }_0^{T_0}|x(t)|\mathrm{d}t$
绝对均值相当于先对原来的信号进行全波整流的处理，然后再求取均值。
有效值：$x_{ms}=\sqrt{\frac{1}{T_0}{\int }_0^{T_0}{x}^2(t)\mathrm{d}t}$
有效值相当于信号的均方根值。
平均功率：$P_{av}=\frac{1}{T_0}{\int }_0^{T_0}{x}^2(t)\mathrm{d}t$

3. 瞬变非周期信号与连续频谱

3.1 傅里叶变换

我们如果把之前得出的2-4代入到2-3之中，我们不难得出：
$$x(t)=\sum _{n=-\infty }^{\infty }\left(\frac{1}{T_0}{\int }_{-\frac{T_0}{2}}^{\frac{T_0}{2}}{\mathrm{e}}^{-\mathrm{j}n{\omega }_{0}t}\mathrm{d}t\right){\mathrm{e}}^{\mathrm{j}n{\omega }_{0}t}\text{\hspace{1em}(3-1)}$$
我们如果在这个情况下让$T_0\to \infty$，我们就可以化求和符号为积分符号。由于有$T_0=2\pi /{\omega }_0$。这个时候${\omega }_0\to 0$，$n{\omega }_0$就变成了一个连续量，我们让$n{\omega }_0=\omega$，则${\omega }_0=\mathrm{d}\omega$。
那么在这种情况下，式2-5就可以被转化为：
$$\begin{array}{rl}x(t)& ={\int }_{-\infty }^{\infty }\frac{\mathrm{d}\omega }{2\pi }{\int }_{-\infty }^{\infty }{\mathrm{e}}^{-\mathrm{j}\omega t}\mathrm{d}t{\mathrm{e}}^{\mathrm{j}\omega t}\\ & ={\int }_{-\infty }^{\infty }\left(\frac{1}{2\pi }{\int }_{-\infty }^{\infty }{\mathrm{e}}^{-\mathrm{j}\omega t}\mathrm{d}t\right){\mathrm{e}}^{\mathrm{j}\omega t}\mathrm{d}\omega \end{array}\text{\hspace{1em}(3-2)}$$
一解我多年来的疑惑啊。
我们规定：
$$X(\omega )=\frac{1}{2\pi }{\int }_{-\infty }^{\infty }{\mathrm{e}}^{-\mathrm{j}\omega t}\mathrm{d}t\text{\hspace{1em}(3-3)}$$
以及
$$x(t)={\int }_{-\infty }^{\infty }X(\omega ){\mathrm{e}}^{\mathrm{j}\omega t}\mathrm{d}\omega \text{\hspace{1em}(3-4)}$$
式3-3表达了$X(\omega )$为$x(t)$的傅里叶变换。(FT, Fourier Transfer)
式3-4表达了$x(t)$为$X(\omega )$的傅里叶逆变换。(IFT, Inverse Fourier Transfer)

---

如果我们改用我们在工程上应用较多的频率的话：
有$\omega =2\pi f$，则：
$$\frac{1}{2\pi }{\int }_{-\infty }^{\infty }{\mathrm{e}}^{-\mathrm{j}\omega t}\mathrm{d}t=\frac{1}{2\pi }{\int }_{-\infty }^{\infty }{\mathrm{e}}^{-\mathrm{j}2\pi ft}\mathrm{d}t$$
令$2\pi t=\tau$，代入其中：
$$\frac{1}{2\pi }{\int }_{-\infty }^{\infty }{\mathrm{e}}^{-\mathrm{j}\omega t}\mathrm{d}t=\frac{1}{2\pi }\frac{1}{2\pi }{\int }_{-\infty }^{\infty }{\mathrm{e}}^{-\mathrm{j}f\tau }\mathrm{d}\tau =\frac{1}{2\pi }{X}^{\prime }(f)$$
为了避免啰嗦，我们索性直接把$X(f)=2\pi X(\omega )$
由此我们就可以得到：
$$\begin{array}{rl}X(f)& ={\int }_{-\infty }^{\infty }x(t){\mathrm{e}}^{-\mathrm{j}2\pi ft}\mathrm{d}t\\ x(t)& ={\int }_{-\infty }^{\infty }X(f){\mathrm{e}}^{\mathrm{j}2\pi ft}\mathrm{d}f\end{array}\text{\hspace{1em}(3-5)}$$
类似于控制工程当中频率特性的幅频特性和相频特性，这里有：频率的连续值谱$|X(f)|$和连续相位谱$\varphi (f)$。
3-5非常重要。

---

后面的一道例题里面介绍了一种函数和他的傅里叶变换。
对于函数：
$$w(t)=\{\begin{array}{ll}1& |t|<\frac{T}{2}\\ 0& |t|>\frac{T}{2}\end{array}\text{\hspace{1em}(3-6)}$$
我们称3-6表示的函数为矩形窗函数。它的频谱为:
$$W(f)=T\frac{\sin \pi fT}{\pi fT}=T\mathrm{s}\mathrm{i}\mathrm{n}\mathrm{c}(\pi fT)$$
注意，这里我们定义了一个新的函数：
$$\mathrm{s}\mathrm{i}\mathrm{n}\mathrm{c}\theta :=\frac{\sin \theta }{\theta }$$
我们称这个函数为采样函数。

3.2 傅里叶变换的主要性质

我觉得这里可以参考之前控工的拉氏变换的性质。
但我还是整理一下：
注意，下面表格讨论的所有内容的一个前提都是有一个傅里叶变换对$x(t)$和$X(f)$

3.2.1 函数的奇偶虚实性

时域	频域
实偶函数	实偶函数
实奇函数	虚奇函数
虚偶函数	虚偶函数
虚奇函数	实奇函数

其实就是，总结一下，不管原来是奇函数函数偶函数，傅里叶变换以后保持性质不变。对于偶函数而言，虚实性也保持不变。但奇函数则会对虚实性进行一个翻转。

3.2.2 线性叠加

3.2.3 对称

$$X(t)\to x(-f)$$

3.2.4 尺度改变

$$x(kt)\to \frac{1}{k}X\left(\frac{f}{k}\right)$$
如果我们在时域上压缩一个信号的话，那么它在频域上频带加宽，幅值降低。

3.2.5 时移

$$x(t\pm t_0)\to X(f){\mathrm{e}}^{\pm \mathrm{j}2\pi f{t}_0}$$
符号是一样的。

3.2.6 频移

$$x(t){\mathrm{e}}^{\mp \mathrm{j}2\pi f{t}_0}\to X(f\pm f_0)$$

3.2.7 翻转

$$x(-t)\to X(-f)$$

3.2.8 共轭

$$x^{\ast }(t)\to X^{\ast }(-f)$$
这边的共轭我的理解应该就是复数的共轭了。为啥我也不知道，姑且记住吧，书上也没说，爱谁谁。

3.2.9 卷积

在某个域卷积之后到了另外一个域就是乘积。这个和拉氏变换时完全一样的，不说了。

3.2.10 微分

$$\begin{gathered} \frac{{\mathrm{d}}^{n}x(t)}{\mathrm{d}{t}^n}\to (\mathrm{j}2\pi f{)}^{n}X(f) \\ (-\mathrm{j}2\pi t{)}^{n}x(t)\to \frac{{\mathrm{d}}^{n}X(f)}{\mathrm{d}{f}^n} \end{gathered}$$

3.2.11 积分

$${\int }_{-\infty }^{t}x(t)\mathrm{d}t\to \frac{1}{\mathrm{j}2\pi f}X(f)$$

3.3 几种典型信号的频谱

提一个采样性质的概念。我们如果让一个$\delta (t)$和任一连续函数$f(t)$相乘时，它的乘积仅在$t=0$处存在。这个地方是一个强度为$f(0)$的$\delta$函数。我们要是对之进行一个积分：
$${\int }_{-\infty }^{\infty }f(t)\delta (t)\mathrm{d}t=f(0)$$
要是对于任意时刻$t_0$而言，类似地：
$${\int }_{-\infty }^{\infty }f(t)\delta (t-t_0)\mathrm{d}t=f(t_0)$$
这样一来，我们就可以对函数进行采样了。

---

关注一下三角函数的频谱。很奇怪的是，这边尝试用拉普拉斯变换套过去好像不太行。但是无论如何先记录一下结论吧。推导过程其实不难。用$\delta (t)$来进行替换然后计算就好了。
$$\begin{gathered} \sin 2\pi f_{0}t\to \mathrm{j}\frac{1}{2}[\delta (f+f_0)-\delta (f-f_0)] \\ \cos 2\pi f_{0}t\to \frac{1}{2}[\delta (f+f_0)+\delta (f-f_0)] \end{gathered}$$